---

引言

来攻坚级数了，其实也不用这么畏难，几年前刚接触时没学会，现在说不定就通了咧。

---

一、常数项级数

1.1 基本概念

常数项级数 —— 设 { a n } \{a_n\} {an​} 为常数列，称 ${\sum }_{n=1}^{\infty }{a}_n$ 为常数项级数。

常数项级数的收敛与发散 —— 称 $S_n=a_1+a_2+\cdots +a_n$ 为级数 ${\sum }_{n=1}^{\infty }{a}_n$ 的部分和，若 ${\lim }_{n\to \infty }{S}_n$ 存在，称级数 ${\sum }_{n=1}^{\infty }{a}_n$ 收敛，令该极限的值为 $S$ ，则称级数收敛于 $S$ 。若该极限不存在，则称级数发散。

1.2 基本性质

性质 1 —— $$\sum _{n=1}^{\infty }{u}_n=A,\sum _{n=1}^{\infty }{v}_n=B,则\sum _{n=1}^{\infty }(u_n\pm v_n)=\sum _{n=1}^{\infty }{u}_n\pm \sum _{n=1}^{\infty }{v}_n=A\pm B.$$

一个收敛的级数加上一个发散的级数，所得结果一定发散。
但是两个发散的级数相加，结果不一定发散。如 $$\sum _{n=1}^{\infty }(-1{)}^n+\sum _{n=1}^{\infty }(-1{)}^{n-1}=0.$$

性质 2 —— $$设\sum _{n=1}^{\infty }{u}_n=S,则\sum _{n=1}^{\infty }k{u}_n=kS.若k\ne 0,两者敛散性相同.$$ 性质 3 —— 级数增加、减少、改变有限项，不改变级数的敛散性，但可能改变级数的和。

性质 4 —— 若一个级数收敛，则任意添加括号后的级数也收敛，反之，若添加括号的级数收敛，则原级数不一定收敛（即添加括号可提高级数收敛的可能性）。

例如，级数 ${\sum }_{n=1}^{\infty }(-1{)}^n$ 发散，但 $(-1+1)+(-1+1)+\dots$ 收敛。

性质 5 —— （级数收敛的必要条件）$$若级数\sum _{n=1}^{\infty }{a}_n收敛，则\underset{n\to \infty }{\lim }{a}_n=0;反之则不一定。$$ 证明： 令 $S_n=a_1+a_2+\cdots +a_n$ ，由级数收敛，可知 ${\lim }_{n\to \infty }{S}_n$ 存在，设其值为 $S$ 。因为 $a_n=S_n-S_{n-1}$ ，所以 $$\underset{n\to \infty }{\lim }{a}_n=\underset{n\to \infty }{\lim }{S}_n-\underset{n\to \infty }{\lim }{S}_{n-1}=S-S=0.$$ 对于级数 ${\sum }_{n=1}^{\infty }1/n$ ，尽管 ${\lim }_{n\to \infty }1/n=0$ ，但其是发散的。

1.3 两个重要级数

1.3.1 p 级数

（1）定义：形如 ${\sum }_{n=1}^{\infty }1/n^p$ 的级数称为 $p$ 级数，当 $p=1$ 时，称 ${\sum }_{n=1}^{\infty }1/n$ 为调和级数。

（2）敛散性判断

1. 当 $p\le 1$ 时，$p$ 级数发散；特别地，调和级数发散；
2. 当 $p>1$ 时，$p$ 级数收敛。

1.3.2 几何级数

（1）定义：形如 ${\sum }_{n=1}^{\infty }a{q}^n(a\ne 0)$ 的级数称为几何级数。

（2）敛散性判断

1. 当 $|q|\ge 1$ 时，几何级数发散；
2. 当 $|q|<1$ 时，几何级数收敛，且其值为 $S=\frac{aq}{1-q}$

1.4 正项级数及其敛散性判断

（一）正项级数的概念

设 ${\sum }_{n=1}^{\infty }{a}_n$ 为常数项级数，若对所有的 $n$ 有 $a_n\ge 0$ ，称其为正项级数。

正项级数的最大特点是部分和数列 { S n } \{S_n\} {Sn​} 单调递增，有两种情形：

1. { S n } \{S_n\} {Sn​} 无上界，则 ${\lim }_{n\to \infty }{S}_n=+\infty$ ，此时正项级数发散；
2. 存在 $M>0$ ，使得 $S_n\le M$ ，此时 ${\lim }_{n\to \infty }{S}_n$ 存在，则正项级数收敛。

（二）正项级数审敛法

我用 Word 敲成表格再截图贴上来吧。

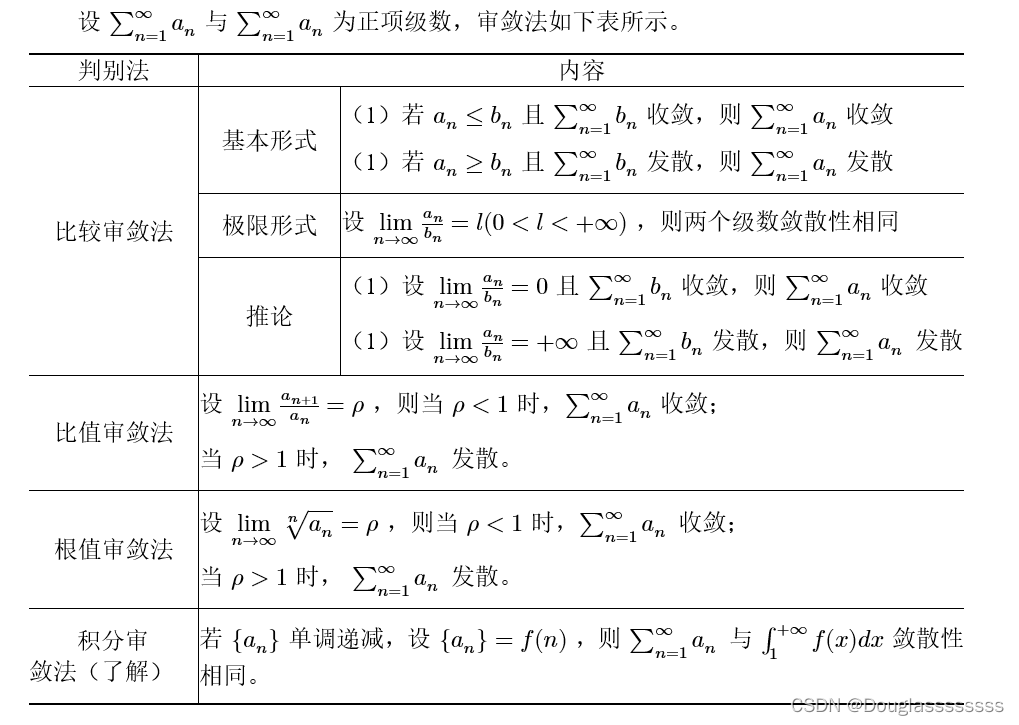
判断正项级数敛散性的一般思路如下：

（1）判断级数是否满足收敛的必要条件，若不满足则级数发散；

（2）若级数一般项是数列相邻两项之差，一般使用定义法；

（3）对一般项满足一定条件的但不具体的正项级数，一般使用使用级数敛散性的性质及判别法；

（4）对一般具体的正项级数，一般使用具体审敛法：若一般项含有阶乘，一般使用比值审敛法；若一般项含有 $n$ 次幂，一般使用根值审敛法；若一般项含有对数，一般使用积分审敛法；其余情形，一般使用比值审敛法。

1.5 交错级数及其审敛法

（一）交错级数的概念

称 ${\sum }_{n=1}^{\infty }(-1{)}^n{u}_n$ 或 ${\sum }_{n=1}^{\infty }(-1{)}^{(n-1)}{u}_n$ 为交错级数，其中 $u_n>0.$

（二）莱布尼兹审敛法

设 ${\sum }_{n=1}^{\infty }(-1{)}^{(n-1)}{u}_n$ 为交错级数，若级数满足以下两个条件：

（1） { u n } \{u_n\} {un​} 单调递减；（2）${\lim }_{n\to \infty }{u}_n=0,$

则称级数 ${\sum }_{n=1}^{\infty }(-1{)}^{(n-1)}{u}_n$ 收敛，且其和不超过 $u_1.$

交错级数收敛的两个条件是充分条件，非必要。

1.6 级数的绝对收敛与条件收敛

（一）基本概念

若 ${\sum }_{n=1}^{\infty }|u_n|$ 收敛，则称 ${\sum }_{n=1}^{\infty }{u}_n$ 绝对收敛。

若 ${\sum }_{n=1}^{\infty }{u}_n$ 收敛，但 ${\sum }_{n=1}^{\infty }|u_n|$ 发散，称 ${\sum }_{n=1}^{\infty }{u}_n$ 条件收敛。

（二）绝对收敛与条件收敛的关系

若 ${\sum }_{n=1}^{\infty }{u}_n$ 绝对收敛，则 ${\sum }_{n=1}^{\infty }{u}_n$ 收敛，反之则不一定。

---

一些笔记和总结：

（1）使用如下口诀可以帮助记忆敛散性判断：添加括号增加级数收敛可能性；一般项趋于 0 的速度越快，级数收敛的可能性越大；添加绝对值，增加收敛可能性。

（2）常数项级数收敛性判断的一班次序：

第一步：看是否满足级数收敛的必要条件；

第二步：看是否可以根据定义判断敛散性；

第三步：确定具体的级数类型，根据前文所述利用各自审敛法判断。

（3）正项级数收敛的充要条件是 ${\sum }_{n=1}^{\infty }{u}_{2n-1}$ 和 ${\sum }_{n=1}^{\infty }{u}_{2n}$ 都收敛。

（4）若 ${\sum }_{n=1}^{\infty }{u}_n$ 收敛 ，则 ${\sum }_{n=1}^{\infty }(u_n+u_{n+1)}$ 一定收敛（添加括号提升收敛可能性）。

（5）若 ${\sum }_{n=1}^{\infty }{u}_n$ 收敛，${\sum }_{n=1}^{\infty }{u}_n^2$ 不一定收敛；但若 ${\sum }_{n=1}^{\infty }{u}_n$ 收敛的正数项级数，${\sum }_{n=1}^{\infty }{u}_n^2$ 一定收敛。

---

写在最后

常数项级数的理论部分就到这里，后面我们继续学习幂级数的内容。