前言

请输入一个表达式：计算式:[7*2*2-5+1-5+3-3]

请问: 计算机底层是如何运算得到结果的？
注意不是简单的把算式列出运算,因为我们看这个算式 7 * 2 * 2 - 5, 但是计算机怎么理解这个算式的(对计算机而言，它接收到的就是一个字符串)，我们讨论的是这个问题

一：基本概念

1.1 介绍

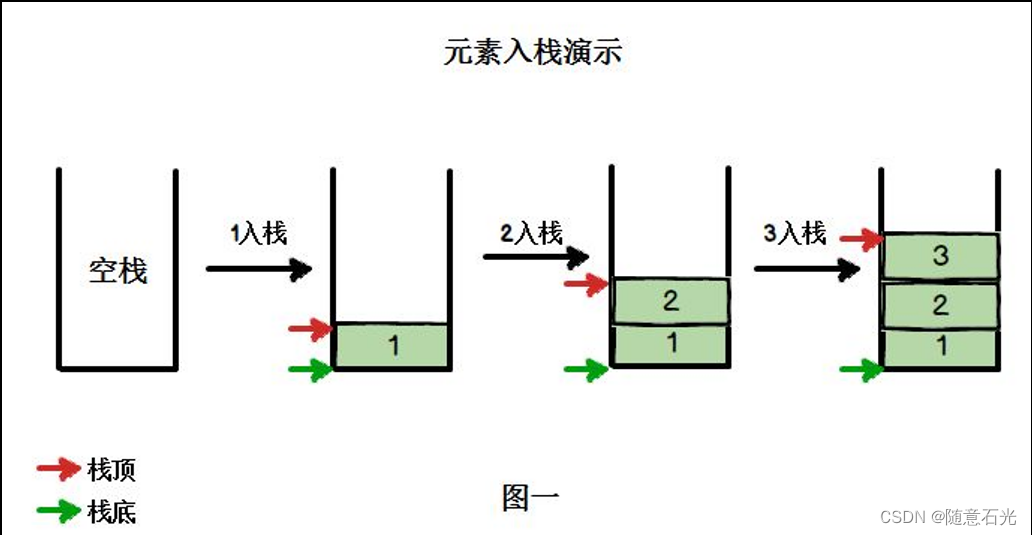
1. 栈的英文为(stack)，栈是一个先入后出(FILO-First In Last Out)的有序列表。
2. 栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端，为变化的一端，称为栈顶(Top)，另一端为固定的一端，称为栈底(Bottom)。
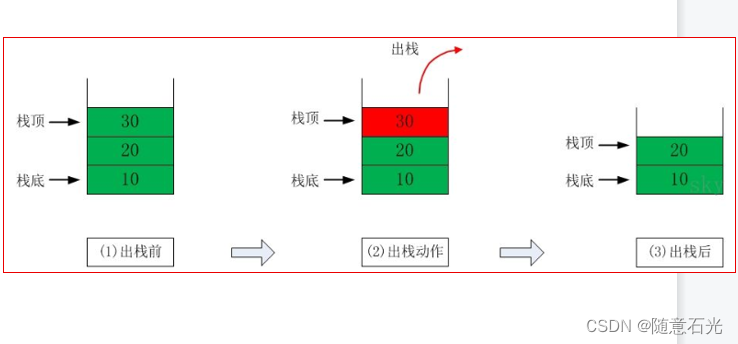
3. 根据栈的定义可知，最先放入栈中元素在栈底，最后放入的元素在栈顶，而删除元素刚好相反，最后放入的元素最先删除，最先放入的元素最后删除

1.2 入栈和出栈示意图

1.3 栈的应用场景

1. 子程序的调用：在跳往子程序前，会先将下个指令的地址存到堆栈中，直到子程序执行完后再将地址取出，以回到原来的程序中。
2. 处理递归调用：和子程序的调用类似，只是除了储存下一个指令的地址外，也将参数、区域变量等数据存入堆栈中。
3. 表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。
4. 二叉树的遍历。
5. 图形的深度优先(depth一first)搜索法。

二：使用数组模拟栈

2.1 思路分析

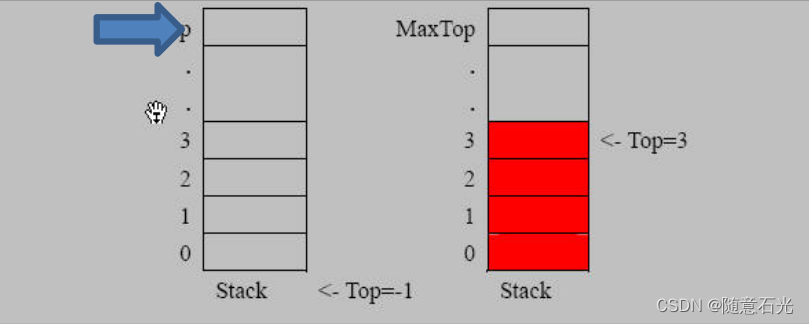
1. 使用数组来模拟栈
2. 定义一个 top 来表示栈顶，初始化 为 -1
3. 入栈的操作，当有数据加入到栈时， top++; stack[top] = data;
4. 出栈的操作， int value = stack[top]; top–, return value

2.2 代码实现

class ArrayStack {

    /**
     * 栈的大小
     */
    private int maxSize;

    /**
     * 存放栈的数据
     * 数组模拟栈
     */
    private int[] stack;

    /**
     * top表示栈顶，初始化为-1
     */
    private int top = -1;


    /**
     * 有参构造
     *
     * @param maxSize
     */
    public ArrayStack(int maxSize) {
        this.maxSize = maxSize;
        //初始化栈
        stack = new int[maxSize];
    }

    /**
     * 判断栈是否满了
     *
     * @return boolean
     */
    public boolean isFull() {
        return top == maxSize - 1;
    }

    /**
     * 判断栈是否为空
     *
     * @return boolean
     */
    public boolean isEmpty() {
        return top == -1;
    }

    /**
     * 入栈
     *
     * @param value
     */
    public void push(int value) {
        //先判断栈是否满了
        if (isFull()) {
            System.out.println("栈满了");
            return;
        }
        top++;
        stack[top] = value;
    }

    /**
     * 出栈-将栈顶的数据返回
     *
     * @return int
     */
    public int pop() {
        //先判断栈是否为空
        if (isEmpty()) {
            throw new RuntimeException("栈是空的");
        }
        //取出栈顶的值
        int value = stack[top];
        top--;
        return value;
    }

    /**
     * 遍历栈
     * 遍历时，需要从栈顶显示数据
     */
    public void list() {
        //先判断栈是否为空
        if (isEmpty()) {
            System.out.println("栈是空的，无法遍历");
            return;
        }
        //从栈顶开始遍历
        for (int i = top; i >= 0; i--) {
            System.out.printf("stack[%d]=%d\n", i, stack[i]);
        }

    }


}

2.3 测试

public class ArrayStackDemo {
    public static void main(String[] args) {
        //测试一下
        //先创建一个ArrayStack对象
        ArrayStack stack = new ArrayStack(4);
        String key = "";
        //控制是否退出菜单
        boolean loop = true;
        Scanner scanner = new Scanner(System.in);
        while (loop) {
            System.out.println("show: 表示显示栈");
            System.out.println("exit: 退出程序");
            System.out.println("push: 表示添加数据到栈(入栈)");
            System.out.println("pop: 表示从栈取出数据(出栈");
            System.out.println("请输入你的选择");
            key = scanner.next();
            switch (key) {
                case "show":
                    stack.list();
                    break;
                case "push":
                    System.out.println("请输入一个数");
                    int value = scanner.nextInt();
                    stack.push(value);
                    break;
                case "pop":
                    try {
                        int res = stack.pop();
                        System.out.printf("出栈的数据是 %dn", res);
                    } catch (Exception e) {
                        System.out.println(e.getMessage());
                    }
                    break;
                case "exit":
                    scanner.close();
                    loop = false;
                    break;
                default:
                    break;

            }
        }
        System.out.println("程序退出");
    }
}

三：使用栈模拟中缀表达式计算器

3.1 整体思路

创建两个栈，一个是数栈专门用来存放数字，另一个是符号栈用来存放符号。

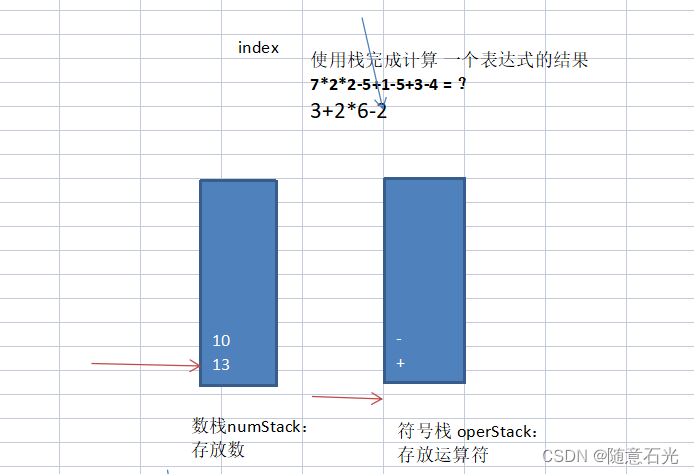
1. 使用一个index值（索引），来遍历我们的表达式
2. 如果我们发现是一个数字，那么就入数栈
3. 如果发现是一个字符，那么就分如下两种情况
   1）如果当前符号栈为空，那么就直接入栈
   2）如果当前符号栈有操作符，就进行比较。如果当前操作符的优先级小于或者等于栈中的操作符，就需要从数栈中pop出两个数，再从符号栈中pop出一个符号，进行运算，将得到的结果，入数栈。然后将当前操作符入符号栈，如果当前的操作符的优先级大于栈中的操作符，则直接入符号栈。
4. 当表达式扫描完毕，就顺序从数栈和符号栈中pop出相应的数和符号，并运行。
5. 最后在数栈中只有一个数字，就是表达式的结果

3.2 验证3+2*6-2=13

3.2.1 定义栈

class ArrayStackCalculator {

    /**
     * 栈的大小
     */
    private int maxSize;

    /**
     * 存放栈的数据
     * 数组模拟栈
     */
    private int[] stack;

    /**
     * top表示栈顶，初始化为-1
     */
    private int top = -1;


    /**
     * 有参构造
     *
     * @param maxSize
     */
    public ArrayStackCalculator(int maxSize) {
        this.maxSize = maxSize;
        //初始化栈
        stack = new int[maxSize];
    }

    /**
     * 判断栈是否满了
     *
     * @return boolean
     */
    public boolean isFull() {
        return top == maxSize - 1;
    }

    /**
     * 判断栈是否为空
     *
     * @return boolean
     */
    public boolean isEmpty() {
        return top == -1;
    }

    /**
     * 入栈
     *
     * @param value
     */
    public void push(int value) {
        //先判断栈是否满了
        if (isFull()) {
            System.out.println("栈满了");
            return;
        }
        top++;
        stack[top] = value;
    }

    /**
     * 出栈-将栈顶的数据返回
     *
     * @return int
     */
    public int pop() {
        //先判断栈是否为空
        if (isEmpty()) {
            throw new RuntimeException("栈是空的");
        }
        //取出栈顶的值
        int value = stack[top];
        top--;
        return value;
    }

    /**
     * 遍历栈
     * 遍历时，需要从栈顶显示数据
     */
    public void list() {
        //先判断栈是否为空
        if (isEmpty()) {
            System.out.println("栈是空的，无法遍历");
            return;
        }
        //从栈顶开始遍历
        for (int i = top; i >= 0; i--) {
            System.out.printf("stack[%d]=%d\n", i, stack[i]);
        }

    }


}

3.2.2 返回运算符的优先级

/**
     * 返回运算符的优先级，优先级使用数字表示
     * 数字越大，优先级越高
     * <p>
     * 假设目前表达式只有 + - * /
     *
     * @return
     */
    public int priority(int str) {
        if (str == '*' || str == '/') {
            return 1;
        } else if (str == '+' || str == '-') {
            return 0;
        } else {
            return -1;
        }
    }

3.2.3 判断是不是一个运算符

    /**
     * 判断是不是一个运算符
     *
     * @param val
     * @return
     */
    public boolean isOpera(char val) {
        return val == '+' || val == '-' || val == '*' || val == '/';
    }

3.2.4 计算方法

/**
     * 计算方法
     *
     * @param num1
     * @param num2
     * @param opera
     * @return
     */
    public int cal(int num1, int num2, char opera) {
        //用于存放计算的结果
        int res = 0;
        switch (opera) {
            case '+':
                res = num1 + num2;
                break;
            case '-':
                res = num2 - num1;
                break;
            case '*':
                res = num1 * num2;
                break;
            case '/':
                res = num2 / num1;
                break;
            default:
                break;
        }
        return res;
    }

3.2.5 查看栈顶的值

/**
     * 查看栈顶的值，并进行返回
     *
     * @return
     */
    public int peek() {
        return stack[top];
    }

3.2.6 存在问题及解决思路

存在问题：
当表达式存在两位数时，入数栈的时候会有问题，例如30+2*8-2。所以如果为数字,则直接入数栈的时候，我们需要优化一下思路。
解决思路：
1.当处理数字入栈时，不能发现是一个数就直接入栈，因为有可能是多位数
2.在处理数字时，需要向expression的表达式的index后再看一位，如果是数字则继续扫描，如果是符号才入栈
3.因此我们需要定义一个变量字符串，用于拼接

3.2.7 核心代码编写

public static void main(String[] args) {
        //需要计算的表达式
        String expression = "3+2*8-2";
        //创建两个栈，一个是数栈，一个是符号栈
        ArrayStackCalculator numStack = new ArrayStackCalculator(20);
        ArrayStackCalculator operaStack = new ArrayStackCalculator(20);
        //定义需要扫描的变量
        int index = 0;
        int num1 = 0;
        int num2 = 0;
        char opera;
        int res = 0;
        //用于拼接多位数
        String keepNum = "";
        //将每次扫描出来的char保存到ch中
        char ch = ' ';
        //使用while语句开始扫描expression
        //此时说明已经扫描到最后一个节点，跳出while循环
        while (index < expression.length()) {
            //依次得到expression的每一个字符
            ch = expression.substring(index, index + 1).charAt(0);
            //判断ch是什么，就做什么处理
            if (operaStack.isOpera(ch)) {
                //如果为运算符
                //判断当前符号栈是否为空
                if (!operaStack.isEmpty()) {
                    //如果当前符号栈有操作符，就进行比较。如果当前操作符的优先级小于或者等于栈中的操作符，就需要从数栈中pop出两个数，
                    //再从符号栈中pop出一个符号进行运算，将得到的结果，入数栈。然后将当前操作符入符号栈，
                    if (operaStack.priority(ch) <= operaStack.priority(operaStack.peek())) {
                        num1 = numStack.pop();
                        num2 = numStack.pop();
                        opera = (char) operaStack.pop();
                        res = numStack.cal(num1, num2, opera);
                        //将计算的结果入数栈
                        numStack.push(res);
                        //将当前操作符入符号栈
                        operaStack.push(ch);
                    } else {
                        //如果当前的操作符的优先级大于栈中的操作符，则直接入符号栈
                        operaStack.push(ch);
                    }
                } else {
                    //如果为空直接入栈
                    operaStack.push(ch);
                }
            } else {
                //如果为数字,则直接入数栈
                //将字符转化为数字，需要-48
                //numStack.push(ch - 48);
                //存在问题：
                //当表达式存在两位数时，入数栈的时候会有问题，例如`30+2*8-2`。所以如果为数字,则直接入数栈的时候，我们需要优化一下思路。
                //解决思路：
                //1.当处理数字入栈时，不能发现是一个数就直接入栈，因为有可能是多位数
                //2.在处理数字时，需要向expression的表达式的index后再看一位，如果是数字则继续扫描，如果是符号才入栈
                //3.因此我们需要定义一个变量字符串，用于拼接
                keepNum += ch;
                //ch如果已经是expression的最后一位，则不要判断下一位，直接入栈
                if (index == expression.length() - 1) {
                    numStack.push(Integer.parseInt(keepNum));
                } else {
                    //判断下一个字符是不是数字，如果是数字，则继续扫描，如果是符号则直接入栈
                    //下一位不是index++，index值不要变
                    if (operaStack.isOpera(expression.substring(index + 1, index + 2).charAt(0))) {
                        //如果后一位是操作符，则入栈
                        numStack.push(Integer.parseInt(keepNum));
                        //此时注意一定要清空keepNum
                        keepNum = "";
                    }
                }
            }
            //让index加一,并且判断是否扫描到expression的最后一位
            index++;
        }
        //当表达式扫描完毕，就顺序从数栈和符号栈中pop出相应的数和符号，并运行
        while (!operaStack.isEmpty()) {
            //如果符号栈为空，则计算到最后的结果，数栈中只有一个数字【结果】
            num1 = numStack.pop();
            num2 = numStack.pop();
            opera = (char) operaStack.pop();
            res = numStack.cal(num1, num2, opera);
            numStack.push(res);
        }
        //将数栈最后的数pop出来
        int result = numStack.pop();
        System.out.printf("表达式%s=%d", expression, result);

    }

四：前缀、中缀、后缀表达式的介绍

4.1 前缀表达式(波兰表达式)

4.1.1 概念

前缀表达式又称波兰式，前缀表达式的运算符位于操作数之前
举例说明： (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6

4.2.2 前缀表达式的计算机求值

从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素 和
次顶元素），并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果

例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:

1. 从右至左扫描，将6、5、4、3压入堆栈
2. 遇到+运算符，因此弹出3和4（3为栈顶元素，4为次顶元素），计算出3+4的值，得7，再将7入栈
3. 接下来是×运算符，因此弹出7和5，计算出7×5=35，将35入栈
4. 最后是-运算符，计算出35-6的值，即29，由此得出最终结果

4.2 中缀表达式

1. 中缀表达式就是常见的运算表达式，如(3+4)×5-6
2. 中缀表达式的求值是我们人最熟悉的，但是对计算机来说却不好操作(前面我们讲的案例就能看的这个问题)，因此，在计算结果时，往往会将中缀表达式转成其它表达式来操作(一般转成后缀表达式）

4.3 后缀表达式（逆波兰表达式）

4.3.1 概念

1. 后缀表达式又称逆波兰表达式,与前缀表达式相似，只是运算符位于操作数之后
2. 中举例说明： (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –
3. 再比如:
   

4.3.2 后缀表达式的计算机求值

从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 和
栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果

例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:

1. 从左至右扫描，将3和4压入堆栈；
2. 遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
3. 将5入栈；
4. 接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
5. 将6入栈；
6. 最后是-运算符，计算出35-6的值，即29，由此得出最终结果

五：后缀表达式（逆波兰计算器）

原表达式：(3+4)×5-6
后缀表达式：3 4 + 5 × 6 -

5.1 思路分析

1. 先将3 4 + 5 × 6 -放入到arrayList中
2. 将arrayList传递给一个方法，遍历arrayList，配合栈完成计算

5.2 代码实现

/**
 * 逆波兰计算器
 *
 * @author ikun
 */
public class PolandNotation {
    public static void main(String[] args) {
        //先定义一个逆波兰表达式
        //(3+4)×5-6  ->  3 4 + 5 × 6 -
        //数字和符号之间空格隔开
        String suffixExpression = "3 4 + 5 * 6 - ";
        //思路
        //1.先将3 4 + 5 × 6 -放入到arrayList中
        //2.将arrayList传递给一个方法，遍历arrayList，配合栈完成计算
        List<String> list = getListString(suffixExpression);
        int res = calculate(list);
        System.out.printf("计算的结为%d", res);
    }

    /**
     * 将一个逆波兰表达式，依次将数据和运算符放入到arrayList中
     *
     * @param suffixExpression 逆波兰表达式
     * @return List<String>
     */
    public static List<String> getListString(String suffixExpression) {
        List<String> list = new ArrayList<>();
        char[] charArray = suffixExpression.toCharArray();
        for (char c : charArray) {
            if (c != ' ') {
                list.add(String.valueOf(c));
            }
        }
        return list;
    }

    /**
     * 完成逆波兰表达式的运算
     * 例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:
     * <p>
     * 1.从左至右扫描，将3和4压入堆栈；
     * 2.遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
     * 3.将5入栈；
     * 4.接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
     * 5.将6入栈；
     * 6.最后是-运算符，计算出35-6的值，即29，由此得出最终结果
     * </p>
     *
     * @return int value
     */
    public static int calculate(List<String> list) {
        //创建栈，只需一个即可
        Stack<String> stack = new Stack<>();
        //遍历list
        for (String item : list) {
            //这里使用正则表达式来取数
            //匹配的是多位数
            if (item.matches("\\d+")) {
                //入栈
                stack.push(item);
            } else {
                //pop出两个数,并运算,再入栈
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                switch (item) {
                    case "+":
                        res = num1 + num2;
                        break;
                    case "-":
                        res = num1 - num2;
                        break;
                    case "*":
                        res = num1 * num2;
                        break;
                    case "/":
                        res = num1 / num2;
                        break;
                    default:
                        throw new RuntimeException("运算符有误");
                }
                //把res入栈
                stack.push(String.valueOf(res));
            }

        }
        //最后stack中的数据就是运算符的结果
        return Integer.parseInt(stack.pop());
    }


}

六：中缀表达式转后缀表达式

大家看到，后缀表达式适合计算式进行运算，但是人却不太容易写出来，尤其是表达式很长的情况下，因此在开发中，我们需要将中缀表达式转成后缀表达式。

6.1 思路分析

1. 初始化两个栈：运算符栈s1和存储中间结果的栈s2；
2. 从左至右扫描中缀表达式；
3. 遇到操作数时，将其压s2；
4. 遇到运算符时，比较其与s1栈顶运算符的优先级：
   1）如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
   2）否则，若优先级比栈顶运算符的高，也将运算符压入s1；
   3）否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4-1)与s1中新的栈顶运算符相比较；
5. 遇到括号时：
   1）如果是左括号“(”，则直接压入s1；
   2）如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
6. 重复步骤2至5，直到表达式的最右边
7. 将s1中剩余的运算符依次弹出并压入s2
8. 依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

6.2 举例说明

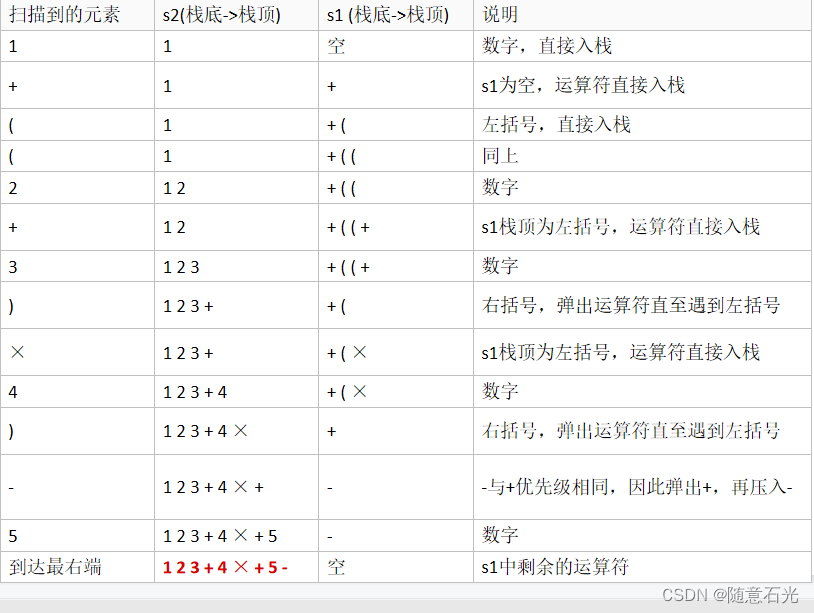
将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式"1 2 3 + 4 × + 5 –"

6.3 代码实现

6.3.1 将一个中缀表达式，依次将数据和运算符放入到arrayList中

/**
     * 将一个中缀表达式，依次将数据和运算符放入到arrayList中
     * expression -> 1+((2+3)*4)-5
     *
     * @param expression 中缀表达式
     * @return List<String>
     */
    public static List<String> toInfixExpressionList(String expression) {
        List<String> list = new ArrayList<>();
        //index表示指针，用于遍历中缀表达式字符串
        int index = 0;
        //对多位数进行拼接
        String str;
        //每遍历一个字符就放到ch中
        char ch;
        do {
            if ((ch = expression.charAt(index)) < 48 || (ch = expression.charAt(index)) > 57) {
                //如果ch是一个字符，则需要添加到list中
                list.add(String.valueOf(ch));
                //index需要向后移
                index++;
            } else {
                str = "";
                //如果是数字，则需要考虑多位数的情况
                while (index < expression.length() && (ch = expression.charAt(index)) >= 48 && (ch = expression.charAt(index)) <= 57) {
                    //拼接字符
                    str += ch;
                    index++;
                }
                list.add(str);
            }

        } while (index < expression.length());
        return list;

    }

6.3.2 返回一个运算符对应的优先级

/**
 * 返回一个运算符对应的优先级
 */
class Operation {

    private static final int ADD = 1;

    private static final int SUB = 1;

    private static final int MUL = 2;

    private static final int DIV = 2;

    /**
     * 返回对应优先级的数字
     *
     * @param operation
     * @return
     */
    public static int getValue(String operation) {
        int result = 0;
        switch (operation) {
            case "+":
                result = ADD;
                break;
            case "-":
                result = SUB;
                break;
            case "*":
                result = MUL;
                break;
            case "/":
                result = DIV;
                break;
            default:
                System.out.println("该运算符不存在");
                break;
        }
        return result;

    }

}

6.3.3 将中缀表达式转化为后缀表达式

/**
     * 将中缀表达式转化为后缀表达式
     *
     * @param infixExpressionList
     * @return
     */
    public static List<String> parseSuffixExpressionList(List<String> infixExpressionList) {
        //符号栈
        Stack<String> charStack = new Stack<>();
        //中间结果栈只有入栈不会出栈，而且需要逆序输出，所以用arrayList代替
        List<String> resultList = new ArrayList<>();
        //遍历infixExpressionList
        for (String item : infixExpressionList) {
            //如果是一个数就加入到结果栈resultList
            if (item.matches("\\d+")) {
                resultList.add(item);
            } else if (item.equals("(")) {
                charStack.add(item);
            } else if (item.equals(")")) {
                //如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
                while (!charStack.peek().equals("(")) {
                    String pop = charStack.pop();
                    resultList.add(pop);
                }
                //此时丢弃charStack里面的“(”
                charStack.pop();
            } else {
                //若item的优先级小于等于符号栈栈顶运算符，则将符号栈顶的运算符弹出并压入到结果栈中
                while (charStack.size() > 0 && Operation.getValue(charStack.peek()) >= Operation.getValue(item)) {
                    String pop = charStack.pop();
                    resultList.add(pop);
                }
                //将item压入到charStack
                charStack.push(item);
            }
        }
        //将符号栈剩余的符号加入到结果栈
        while (charStack.size() > 0) {
            String pop = charStack.pop();
            resultList.add(pop);
        }
        //因为是list所以按顺序输出就是对应的波兰表达式
        return resultList;
    }

6.3.4 完成逆波兰表达式的运算

/**
     * 完成逆波兰表达式的运算
     * 例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:
     * <p>
     * 1.从左至右扫描，将3和4压入堆栈；
     * 2.遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
     * 3.将5入栈；
     * 4.接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
     * 5.将6入栈；
     * 6.最后是-运算符，计算出35-6的值，即29，由此得出最终结果
     * </p>
     *
     * @return int value
     */
    public static int calculate(List<String> list) {
        //创建栈，只需一个即可
        Stack<String> stack = new Stack<>();
        //遍历list
        for (String item : list) {
            //这里使用正则表达式来取数
            //匹配的是多位数
            if (item.matches("\\d+")) {
                //入栈
                stack.push(item);
            } else {
                //pop出两个数,并运算,再入栈
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                switch (item) {
                    case "+":
                        res = num1 + num2;
                        break;
                    case "-":
                        res = num1 - num2;
                        break;
                    case "*":
                        res = num1 * num2;
                        break;
                    case "/":
                        res = num1 / num2;
                        break;
                    default:
                        throw new RuntimeException("运算符有误");
                }
                //把res入栈
                stack.push(String.valueOf(res));
            }

        }
        //最后stack中的数据就是运算符的结果
        return Integer.parseInt(stack.pop());
    }


}

6.3.5 完整代码奉上

package com.sysg.dataStructuresAndAlgorithms.stack;

import java.util.*;


/**
 * 逆波兰计算器
 *
 * @author ikun
 */
public class PolandNotation {

    public static void main(String[] args) {
        //说明
        //1.将中缀表达式转化为后缀表达式
        //2.将1+((2+3)*4)-5  ->  1 2 3 + 4 * + 5 –
        //3.首先将1+((2+3)×4)-5转化为对应的list，即['1','+','(','(','2','+','3',')','*','4',')','-','5']
        String expression = "1+((2+3)*4)-5";
        List<String> infixExpressionList = toInfixExpressionList(expression);
        System.out.println("中缀表达式：" + infixExpressionList);
        //4.将中缀表达式转化为后缀表达式
        List<String> suffixStringList = parseSuffixExpressionList(infixExpressionList);
        System.out.println("后缀表达式：" + suffixStringList);
        //数字和符号之间空格隔开
        //String suffixExpression = "3 4 + 5 * 6 -";
        //思路
        //1.先将3 4 + 5 * 6 -放入到arrayList中
        //2.将arrayList传递给一个方法，遍历arrayList，配合栈完成计算
        //List<String> suffixStringList = getListSuffixString(suffixExpression);
        int res = calculate(suffixStringList);
        System.out.printf("计算的结为%d", res);
    }

    /**
     * 将中缀表达式转化为后缀表达式
     *
     * @param infixExpressionList
     * @return
     */
    public static List<String> parseSuffixExpressionList(List<String> infixExpressionList) {
        //符号栈
        Stack<String> charStack = new Stack<>();
        //中间结果栈只有入栈不会出栈，而且需要逆序输出，所以用arrayList代替
        List<String> resultList = new ArrayList<>();
        //遍历infixExpressionList
        for (String item : infixExpressionList) {
            //如果是一个数就加入到结果栈resultList
            if (item.matches("\\d+")) {
                resultList.add(item);
            } else if (item.equals("(")) {
                charStack.add(item);
            } else if (item.equals(")")) {
                //如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
                while (!charStack.peek().equals("(")) {
                    String pop = charStack.pop();
                    resultList.add(pop);
                }
                //此时丢弃charStack里面的“(”
                charStack.pop();
            } else {
                //若item的优先级小于等于符号栈栈顶运算符，则将符号栈顶的运算符弹出并压入到结果栈中
                while (charStack.size() > 0 && Operation.getValue(charStack.peek()) >= Operation.getValue(item)) {
                    String pop = charStack.pop();
                    resultList.add(pop);
                }
                //将item压入到charStack
                charStack.push(item);
            }
        }
        //将符号栈剩余的符号加入到结果栈
        while (charStack.size() > 0) {
            String pop = charStack.pop();
            resultList.add(pop);
        }
        //因为是list所以按顺序输出就是对应的波兰表达式
        return resultList;
    }


    /**
     * 将一个中缀表达式，依次将数据和运算符放入到arrayList中
     * expression -> 1+((2+3)*4)-5
     *
     * @param expression 中缀表达式
     * @return List<String>
     */
    public static List<String> toInfixExpressionList(String expression) {
        List<String> list = new ArrayList<>();
        //index表示指针，用于遍历中缀表达式字符串
        int index = 0;
        //对多位数进行拼接
        String str;
        //每遍历一个字符就放到ch中
        char ch;
        do {
            if ((ch = expression.charAt(index)) < 48 || (ch = expression.charAt(index)) > 57) {
                //如果ch是一个字符，则需要添加到list中
                list.add(String.valueOf(ch));
                //index需要向后移
                index++;
            } else {
                str = "";
                //如果是数字，则需要考虑多位数的情况
                while (index < expression.length() && (ch = expression.charAt(index)) >= 48 && (ch = expression.charAt(index)) <= 57) {
                    //拼接字符
                    str += ch;
                    index++;
                }
                list.add(str);
            }

        } while (index < expression.length());
        return list;

    }

    /**
     * 将一个后缀表达式，依次将数据和运算符放入到arrayList中
     *
     * @param suffixExpression 逆波兰表达式
     * @return List<String>
     */
    public static List<String> getListSuffixString(String suffixExpression) {
        List<String> list = null;
        String[] str = suffixExpression.split(" ");
        list = Arrays.asList(str);
        return list;
    }

    /**
     * 完成逆波兰表达式的运算
     * 例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:
     * <p>
     * 1.从左至右扫描，将3和4压入堆栈；
     * 2.遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
     * 3.将5入栈；
     * 4.接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
     * 5.将6入栈；
     * 6.最后是-运算符，计算出35-6的值，即29，由此得出最终结果
     * </p>
     *
     * @return int value
     */
    public static int calculate(List<String> list) {
        //创建栈，只需一个即可
        Stack<String> stack = new Stack<>();
        //遍历list
        for (String item : list) {
            //这里使用正则表达式来取数
            //匹配的是多位数
            if (item.matches("\\d+")) {
                //入栈
                stack.push(item);
            } else {
                //pop出两个数,并运算,再入栈
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                switch (item) {
                    case "+":
                        res = num1 + num2;
                        break;
                    case "-":
                        res = num1 - num2;
                        break;
                    case "*":
                        res = num1 * num2;
                        break;
                    case "/":
                        res = num1 / num2;
                        break;
                    default:
                        throw new RuntimeException("运算符有误");
                }
                //把res入栈
                stack.push(String.valueOf(res));
            }

        }
        //最后stack中的数据就是运算符的结果
        return Integer.parseInt(stack.pop());
    }


}

/**
 * 返回一个运算符对应的优先级
 */
class Operation {

    private static final int ADD = 1;

    private static final int SUB = 1;

    private static final int MUL = 2;

    private static final int DIV = 2;

    /**
     * 返回对应优先级的数字
     *
     * @param operation
     * @return
     */
    public static int getValue(String operation) {
        int result = 0;
        switch (operation) {
            case "+":
                result = ADD;
                break;
            case "-":
                result = SUB;
                break;
            case "*":
                result = MUL;
                break;
            case "/":
                result = DIV;
                break;
            default:
                System.out.println("该运算符不存在");
                break;
        }
        return result;

    }

}