空间曲线的参数方程

二维直线

经过一点$P(x_0，y_0)$的方向向量为$n(cos\theta ，sin\theta )$的直线参数方程为：
$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}{x}_0\\ y_0\end{array}\right]+t\left[\begin{array}{c}cos\theta \\ sin\theta \end{array}\right]t\in [0，2\pi )$$

三维直线

经过一点$P(x_0，y_0，z_0)$的单位方向向量为$n(i,j,k)$的直线参数方程为：
$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}{x}_0\\ y_0\\ z_0\end{array}\right]+t\left[\begin{array}{c}i\\ j\\ k\end{array}\right]t\in [0，2\pi )$$

二维圆

经过圆心$P(x_0，y_0)$，半径为$r$，的圆参数方程为：

$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}{x}_0\\ y_0\end{array}\right]+r\left[\begin{array}{c}cos\theta \\ sin\theta \end{array}\right]\theta \in [0，2\pi )$$

三维圆

经过圆心$P(x_0，y_0，z_0)$，半径为$r$，且该圆所在的平面正交的两个单位向量$\overrightarrow{e_1}(a_x,a_y,a_z),\overrightarrow{e_2}(b_x,b_y,b_z)$的圆参数方程为：

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}{x}_0\\ y_0\\ z_0\end{array}\right]+rcos\theta \left[\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right]+rsin\theta \left[\begin{array}{c}{b}_x\\ b_y\\ b_z\end{array}\right]\theta \in [0，2\pi )$$

特殊情况下，当$\overrightarrow{e_1}(a_x,a_y,a_z),\overrightarrow{e_2}(b_x,b_y,b_z)$分别为$\overrightarrow{e_1}(1,0,0),\overrightarrow{e_2}(0,1,0)$时，公式(4) 简化为：

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}{x}_0\\ y_0\\ z_0\end{array}\right]+r\left[\begin{array}{c}cos\theta \\ sin\theta \\ 0\end{array}\right]\theta \in [0，2\pi )$$

任意平面内的圆，可以先计算基准坐标系中的圆然后通过坐标变换 ，将问题转化为，转换为所求平面内的圆。

图形化表示：

如何快速求解$\overrightarrow{e_1}(a_x,a_y,a_z),\overrightarrow{e_2}(b_x,b_y,b_z)$？

1. 求解$\overrightarrow{e_1}$，将圆所在平面的法向量与坐标向量$\vec{i}$叉乘，然后单位化即可得到，如果叉乘结果为0 ，就叉乘$\vec{j}$，再者就叉乘$\vec{k}$；
2. 求解$\overrightarrow{e_2}$，就将法向量与$\overrightarrow{e_1}$叉乘即可。

对应的python代码：

\sum_{s}^{}  {\textstyle \sum_{}^{}} # 对应的版本matplotlib                3.7.1           py311h06a4308_1
from matplotlib import pyplot as plt
import numpy as np

normal_direction = np.array([1, 1, 1])
radius = 1
center = np.array([1, 1, 1])
pi = 3.1415926
theta = np.array([])

for i in range(100):
    theta = np.append(theta, 2.0 * pi * i / 100)

theta = np.array(theta)
e1 = np.cross(normal_direction, [0, 1, 0])
if np.linalg.norm(e1) < 1e-10:
    e1 = np.cross(normal_direction, [0, 1, 0])

e2 = np.cross(normal_direction, e1)

# 单位化
e1_norm = e1 / np.linalg.norm(e1)
e2_norm = e2 / np.linalg.norm(e2)
size = np.size(theta)

x0 = center[0] * np.ones(size)
y0 = center[1] * np.ones(size)
z0 = center[2] * np.ones(size)

x = x0 + radius * e1[0] * np.cos(theta) + radius * e2[0] * np.sin(theta)
y = y0 + radius * e1[1] * np.cos(theta) + radius * e2[1] * np.sin(theta)
z = z0 + radius * e1[2] * np.cos(theta) + radius * e2[2] * np.sin(theta)

# 建立画布
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.set_xlim(-2, 6)
ax.set_ylim(-2, 6)
ax.set_zlim(-2, 6)

ax.plot3D(x, y, z, 'r')
plt.show()

print("YES PF！")

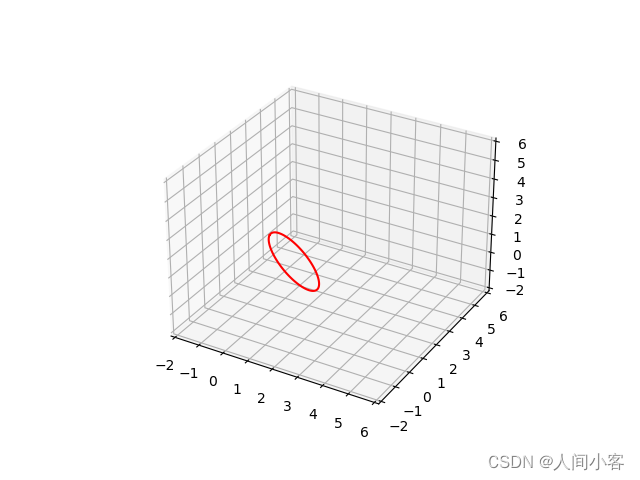
对应的MATLAB代码

Figure_1normal=[1 1 1]; %法向量n
radius=1; %圆的半径为1
center=[1 1 1]; %圆心的坐标
theta=(0:2*pi/100:2*pi)'; %theta角从0到2*pi

e1=cross(normal,[1 0 0]); %n与i叉乘，求取a向量
if ~any(e1) %如果a为零向量，将n与j叉乘
    e1=cross(normal,[0 1 0]);
end

e2=cross(normal,e1); %求取b向量
e1=e1/norm(e1); %单位化a向量
e2=e2/norm(e2); %单位化b向量

x0=center(1)*ones(size(theta,1),1);
y0=center(2)*ones(size(theta,1),1);
z0=center(3)*ones(size(theta,1),1);

x=x0+radius*e1(1)*cos(theta)+radius*e2(1)*sin(theta);%圆上各点的x坐标
y=y0+radius*e1(2)*cos(theta)+radius*e2(2)*sin(theta);%圆上各点的y坐标
z=z0+radius*e1(3)*cos(theta)+radius*e2(3)*sin(theta);%圆上各点的z坐标

plot3(x,y,z)
xlabel('x轴')
ylabel('y轴')
zlabel('z轴')

三维椭圆

在实际工程化的应用的时候，往往不是圆，而是退化成椭圆，甚至退化成一条直线。

工程中更多是使用椭圆模型，通过检测到的点来确定椭圆的参数，最后确定椭圆的中心点和方向向量。

三维椭圆的参数方程易知：
$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}{x}_0\\ y_0\\ z_0\end{array}\right]+acos\theta \left[\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right]+bsin\theta \left[\begin{array}{c}{b}_x\\ b_y\\ b_z\end{array}\right]\theta \in [0，2\pi )$$
其中$a，b$分别表示为椭圆的长半轴长度，短半轴长度 。其余跟圆类似不作具体说明。

椭圆一般化方程为：
$$c_1{x}^2+c_{2}xy+c_3{y}^2+c_{4}x+c_{5}y+c_6=0$$
可以看到至少使用五个不同点可以确定这六个参数。

一般情况是点的个数远超过5个，处理步骤为：

1. 首先使用RANSAC筛选异常点

2. 构建误差$d_i=c_1{x}^2+c_{2}xy+c_3{y}^2+c_{4}x+c_{5}y+c_6$

3. 构建代价函数，使用最小二乘求解// 或者SVD分解
   $$c_i=argmin\Sigma d_j^{2}s,t\{\begin{array}{c}{\sum }_{i=1}^6{c}_i^2=1\\ i\in [1,6],\\ j\in [1,n]\end{array}$$

4. 假设获得$c_i$ ，求解对应的圆心和法向量

   使用二次型构造，对称矩阵，进行分解，则特征值满足：
   $${\lambda }_1\ge {\lambda }_2>0>{\lambda }_3$$
   如果不满足，改变构造的对称矩阵的符号，重新求解对特征值

   这里直接给出结论：

   $H$为分解矩阵后的特征向量组成的正交矩阵，法向量$\vec{n}$，和中心点$P$为：
   $$\begin{gathered} co{s}^2\phi =\frac{{\lambda }_2-{\lambda }_3}{{\lambda }_1-{\lambda }_3} \\ \vec{n}=\pm H\left[\begin{array}{c}-sin\phi \\ 0\\ cos\phi \end{array}\right] \\ P=\pm H\left[\begin{array}{c}-\sqrt{{\lambda }_3/{\lambda }_1}sin\phi \\ 0\\ \sqrt{-{\lambda }_1/{\lambda }_3}cos\phi \end{array}\right] \end{gathered}$$

参考链接：

1. 空间曲线参数方程
2. 空间圆的方程