前言：在部分大厂笔试时经常会使用OJ题目，这里对《华为机试》和《剑指offer》中的部分题目进行思路分析和讲解，希望对各位读者有所帮助。

题目来自牛客网，欢迎各位积极挑战：

HJ73:计算日期到天数转换_牛客网

JZ17:打印从1到最大的n位数_牛客网

HJ76:尼科彻斯定理_牛客网

目录

HJ73 计算日期到天数转换

题目相关消息

题目描述

输入描述 

输出描述 

示例

 分析问题解决思路

具体实现细节： 

 完整代码实现

JZ17 打印从1到最大的n位数

题目相关消息

描述

示例

分析问题解决思路

具体实现细节

 完整代码实现

HJ76 尼科彻斯定理

题目相关信息

题目描述

 输入描述

输出描述

示例 

分析问题解决思路 

具体实现细节

完整代码实现

---

HJ73 计算日期到天数转换

题目相关消息

题目描述

根据输入的日期，计算是这一年的第几天。

保证年份为4位数且日期合法。

进阶：时间复杂度： O(n) ，空间复杂度： O(1) 

输入描述 

输入一行，每行空格分割，分别是年，月，日

输出描述 

输出是这一年的第几天

示例

输入：2012 12 31

输出：366

输入：1982 3 4

输出：63

 分析问题解决思路

题目让我们输出有多少天，只要解决了以下俩个小问题，问题就迎刃而解了

1. 闰年的情况，我们需要判断输入是否是闰年，在闰年内，2月是29天，这是与正常平年不同的情况，因此我们需要设计和函数来判断是否是闰年
2. 我们在判断的时候应该使用累加的思想，从1月累加到目标月，但是值得注意的一点是，目标月不能直接加当前月份总的天数，应该加上用户输入的天数

具体实现细节： 

        首先我们需要先设计一个判断闰年的函数，如果是闰年就返回1，不是就返回0，方便后续进行调用判断：

int judgeleapyear(int year)
{
	if ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0))
	{
		return 1;
	}
	else
		return 0;
}

        主函数方面，我们定义一个整形变量 days 来记录从这一年的第一天到现在一共有多少天，定义 year, month, day三个整形变量分别来记录用户输入的值,从一月开始遍历到目标月，不包含目标月，如果是大月 days 就加31，如果是小月就加30，另外在2月的时候，使用一个 if 语句来判断当前 2 月有多少天

        //大月
		if ((months == 1) || (months == 3) || (months == 5) || (months == 7) || (months == 8) || (months == 10) || (months == 12))
		{
			days += 31;
		}
		//小月
		else if ((months == 4) || (months == 6) || (months == 9) || (months == 11))
		{
			days += 30;
		}
		//二月
		else
		{
			//润年
			if (ret == 1)
			{
				days += 29;
			}
			//平年
			else
			{
				days += 28;
			}
		}

 完整代码实现

//HJ73
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

int judgeleapyear(int year)
{
	if ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0))
	{
		return 1;
	}
	else
		return 0;
}

int main()
{
	int year = 0;
	int month = 0;
	int day = 0;
	int days = 0;
	scanf("%d %d %d", &year, &month, &day);

	//判断是否是闰年
	int ret = judgeleapyear(year);

	//从一月加到目标月
	for (int months = 1; months < month; months++)
	{
		//大月
		if ((months == 1) || (months == 3) || (months == 5) || (months == 7) || (months == 8) || (months == 10) || (months == 12))
		{
			days += 31;
		}
		//小月
		else if ((months == 4) || (months == 6) || (months == 9) || (months == 11))
		{
			days += 30;
		}
		//二月
		else
		{
			//润年
			if (ret == 1)
			{
				days += 29;
			}
			//平年
			else
			{
				days += 28;
			}
		}
	}

	days += day;
	printf("%d", days);


	return 0;
}

---

JZ17 打印从1到最大的n位数

题目相关消息

描述

        输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

1.  用返回一个整数列表来代替打印
2.  n 为正整数，0 < n <= 5

示例

输入：1

返回值：[1,2,3,4,5,6,7,8,9]

        注意，这道题目是接口题，我们只需要完善题目给出的函数就可以了，将需要返回的值返回就完成了

int* printNumbers(int n, int* returnSize)
{

}

分析问题解决思路

        首先，我们需要明确一件事，这道题是接口题，我们不能像普通的 ACM 模式的题那样写个循环直接打印，我们需要将数据放在一块空间内，然后将其返回

        既然是要放在空间内，那我们就使用 malloc 函数来动态开辟空间，最后在这些空间内逐个赋值就可以了

具体实现细节

        首先我们得先明确数值的范围，如下所示的过程中，我们不难发现，这是次方的关系，也就是说 10^n-1 就是数值的最大值

• 1 位数的数值就是 1~9
• 2 位数的数值就是 1~99
• 3 位数的数值就是 1~999
• 4 位数的数值就是 1~9999

        那么在这里我们就使用 <math.h> 头文件中的库函数 pow 来实现次方的效果，这样我们就获得了数值的大小范围

    //返回数组元素的个数
    *returnSize = pow(10, n) - 1;

        接下来就是动态分配空间，在这里需要注意的是要进行强制类型转化，不然会因为前后类型不一致导致 bug，一个整形大小是 sizeof（int），一共有 *returnsize 个整形

     //动态分配空间
    int* arr = (int*)malloc(*returnSize * sizeof(int));//malloc(字节数)

最后赋值就非常简单了，使用 for 循环实现就可以了

    //赋值
    for (int i = 0; i < *returnSize; ++i)
    {
        *(arr + i) = i + 1;
    }

 完整代码实现

int* printNumbers(int n, int* returnSize)
{
    //返回数组元素的个数
    *returnSize = pow(10, n) - 1;
    //动态分配空间
    int* arr = (int*)malloc(*returnSize * sizeof(int));//malloc(字节数)
    //赋值
    for (int i = 0; i < *returnSize; ++i)
    {
        *(arr + i) = i + 1;
    }
    //返回
    return arr;
}

---

HJ76 尼科彻斯定理

题目相关信息

题目描述

验证尼科彻斯定理，即：任何一个整数m的立方都可以写成m个连续奇数之和

例如：

1^3=1

2^3=3+5

3^3=7+9+11

4^3=13+15+17+19

输入一个正整数m（m≤100），将m的立方写成m个连续奇数之和的形式输出

数据范围： 1≤m≤100 

进阶：时间复杂度：O(m) ，空间复杂度：O(1) 

 输入描述

输入一个int整数

输出描述

输出分解后的string

示例 

输入：6

输出：31+33+35+37+39+41

分析问题解决思路 

首先，我们必须得理解这个题目背后的数学原理，我们举例如下

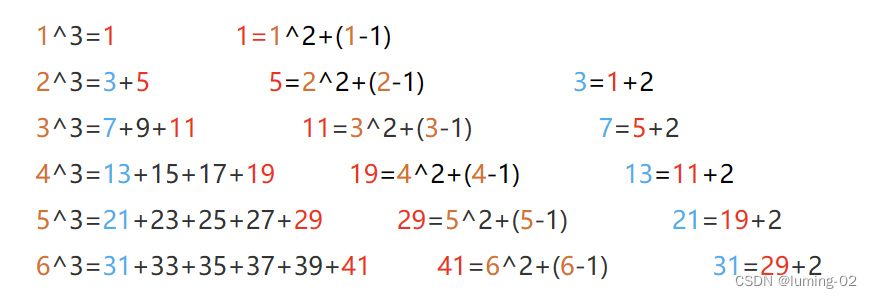
        我们会发现，在多项式中的第一项和最后一项是有迹可循的，我们对于第一项和最后一项的总结如下

1. 第一项：(n-1)^2+((n-1)-1)+2
2. 最后一项：n^2+(n-1)

具体实现细节

我们先使用俩个变量来找到刚才所描述的第一项和最后一项

	int m_first = 0;
	int m_end = 0;

	m_first = (m - 1) * (m - 1) + (((m - 1) - 1) + 2);
	m_end = (m * m) + (m - 1);

        在找到第一项后，我们就可以使用遍历累加来打印了，在尼科彻斯定理表示的多项式中，多项式的数量和要表达的整数m是一样的，都是m，基于此，我们就可以使用循环了，每一次都打印一个奇数，然后在让这个奇数加 2，最后再直接打印最后一项

	for (int i = 0; i < (m - 1); i++)
	{
		printf("%d+", m_first);
		m_first += 2;
	}
	printf("%d", m_end);

完整代码实现

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<math.h>

void math_N(int m)
{
	int m_first = 0;
	int m_end = 0;

	m_first = (m - 1) * (m - 1) + (((m - 1) - 1) + 2);
	m_end = (m * m) + (m - 1);

	for (int i = 0; i < (m - 1); i++)
	{
		printf("%d+", m_first);
		m_first += 2;
	}
	printf("%d", m_end);
}

int main()
{
	int m = 0;
	scanf("%d", &m);

	math_N(m);

	return 0;
}

本次分享就到此结束了，希望我的分享对您有所帮助