目录
- 逻辑回归
- 判别模型(discriminative model)
- 设计模型Function set
- 设计函数选择最好的w和b
- 更新参数w和b
- 逻辑回归与线性回归对比
- 逻辑回归为什么用交叉熵来找最优的参数而不用MAE或MSE
- GM与DM区别
- 判别模型(discriminative model)
- 多维分类——以三类别为例
- GM 生成模型
- DM 判别模型
- 输入特征处理→深度学习
逻辑回归
视频链接
https://www.bilibili.com/video/BV1Wv411h7kN/?p=17&spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=ef8c99c8c4165aea8f811dafa9772ecd
之前博客 一篇博客详解朴素贝叶斯解分类问题 讲到的是采用概率的方法求解w和b去解分类问题,叫做生成模型(Generative Model),除了这种方法外,还可以直接求解w和b,这种方法叫做判别模型(discriminative model)
判别模型(discriminative model)
判别模型的设计仍分为三步
设计模型Function set
f w , b = σ ( ∑ i w i x i + b ) , σ ( x ) = 1 1 + e − x f_{w,b}=\sigma(\sum _iw_ix_i+b),\sigma(x)=\frac 1 {1+e^{-x}} fw,b=σ(i∑wixi+b),σ(x)=1+e−x1
加入sigmoid函数,会使得输出值在0~1之间
设计函数选择最好的w和b
这里采用了似然函数进行计算,似然函数的定义是所有训练数据根据其所属类别以及模型函数的预测乘积(对于Binary分类,若Function是定义的类别C1,则若数据属于C1则直接乘预测函数即可,若属于C2,则乘以(1-预测函数)),这样似然函数的最大值即对应最好的w,b
上述形式计算起来复杂度较高,可以利用ln函数将乘法转换为加法,化简过程如下:
l o s s = − ∑ i n [ y ′ i l n y i + ( 1 − y ′ i ) ( 1 − l n y i ) ] loss=-\sum _i ^n [y^{'i}lny^i+(1-y^{'i})(1-lny^i)] loss=−i∑n[y′ilnyi+(1−y′i)(1−lnyi)]
更新参数w和b
更新参数仍采用gradient descent方法
以更新w为例,求导过程以及更新参数表达式如下:
w n e w = w o l d − η [ − ∑ i ( y i − f w , b ( x i ) ) x j i ] w_{new}=w_{old}-\eta [-\sum _i(y^i-f_{w,b}(x^i))x_j^i] wnew=wold−η[−i∑(yi−fw,b(xi))xji]
逻辑回归与线性回归对比
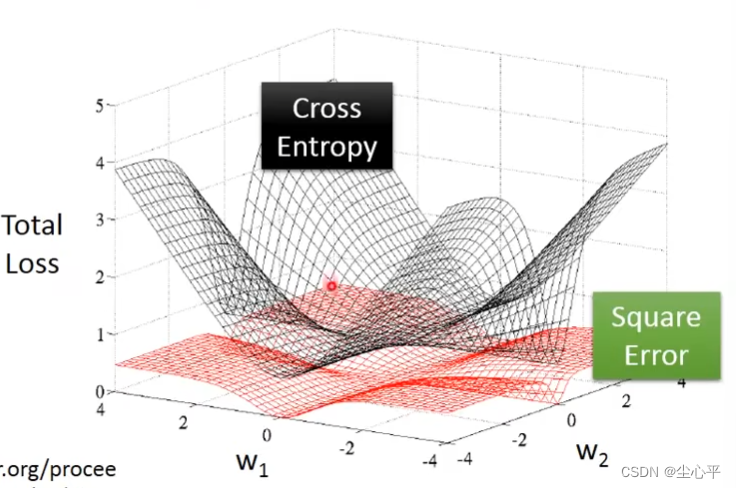
逻辑回归为什么用交叉熵来找最优的参数而不用MAE或MSE
上图为交叉熵和MSE的loss三维变化图,其中黑色为交叉熵,红色为MSE。可以观察到MSE的曲面整体较为平滑,随机选取一个点作为开始值,若离实际相差较大,但因曲面平缓,偏导斜率较小,更新参数会比较慢。而交叉熵曲面较为曲折,对于有与实际相差较大的地方,斜率也大,参数更新会比较快。
GM与DM区别
GM全称是生成模型 Generative
Model,其主要是利用后验概率去求解分类问题即求解P(C1|x),具体是先假设样本是采取某种概率分布从而表示出P(x|C1),紧接着利用条件概率公式即可计算出P(C1|x)。DM全称是判别模型Discriminative
Model,这个方法是并没有做任何的假设,直接求解P(C1|x),定义其模型并按照正常的线性回归三步骤去解。两种方法模型,最后都可以求解出sigmoid(wx+b) 的形式,但参数一般不同。
一般而言,随着数据集的增加,DM比GM的准确率更好。以下图为例,采用条件概率 GM计算测试集属于哪一个类别时,会与想象情况不太一样。
多维分类——以三类别为例
GM 生成模型
每一个类别都有自己的一个根据分布确定的生成函数,分布函数根据自己类别的样本数据的均值确定μ,根据所有类别的样本数据的各自的Σ
结合每个类别样本在所有样本中的比率确定最终的Σ。
根据确定的生成函数以及条件概率公式确定出选择一个样本它属于这个类的后验概率函数,若该函数值
大于0.5则可认为是该类别,否则认为不是该类别。 将测试样本作为每一个类别的后验概率函数输入,即可得到该测试样本属于每一个类别的概率。
DM 判别模型
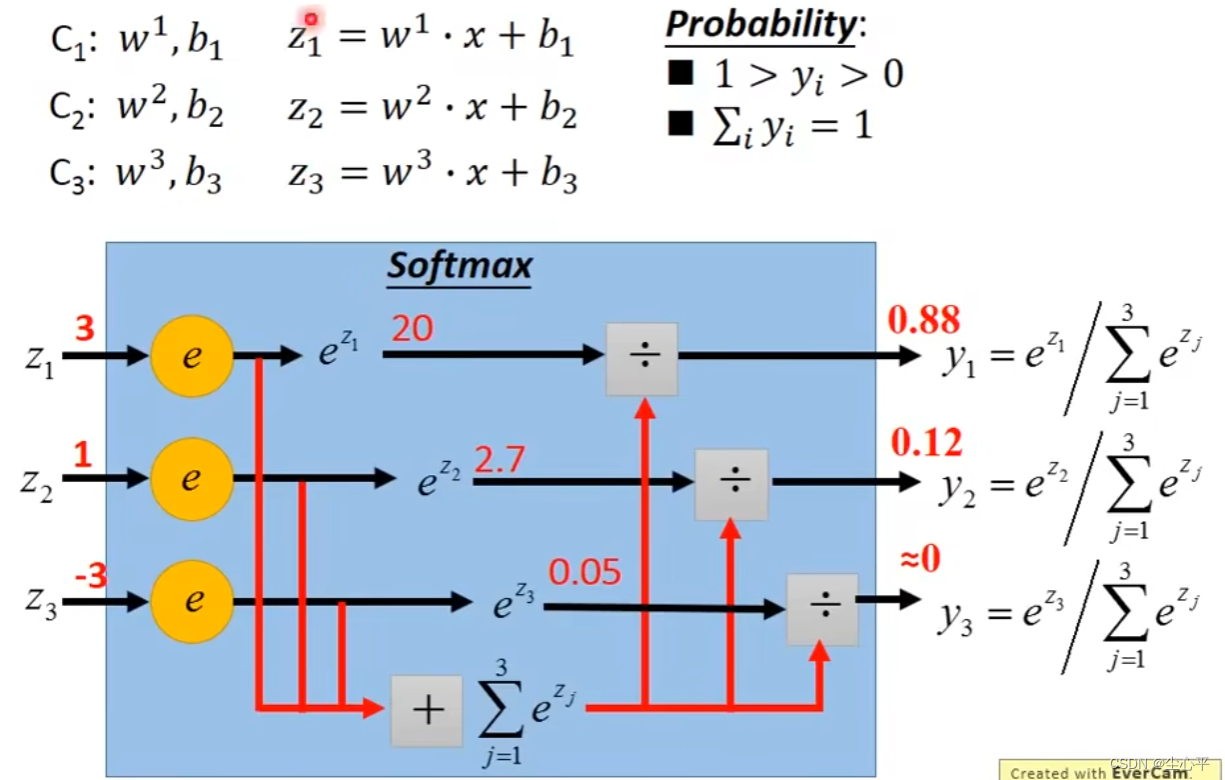
主要与二分类的区别是,最后的输出采用softmax函数。有n个类别,就有n个w向量和b,有n个z方程,输出n维向量,向量值中最大的即为对应的类别。
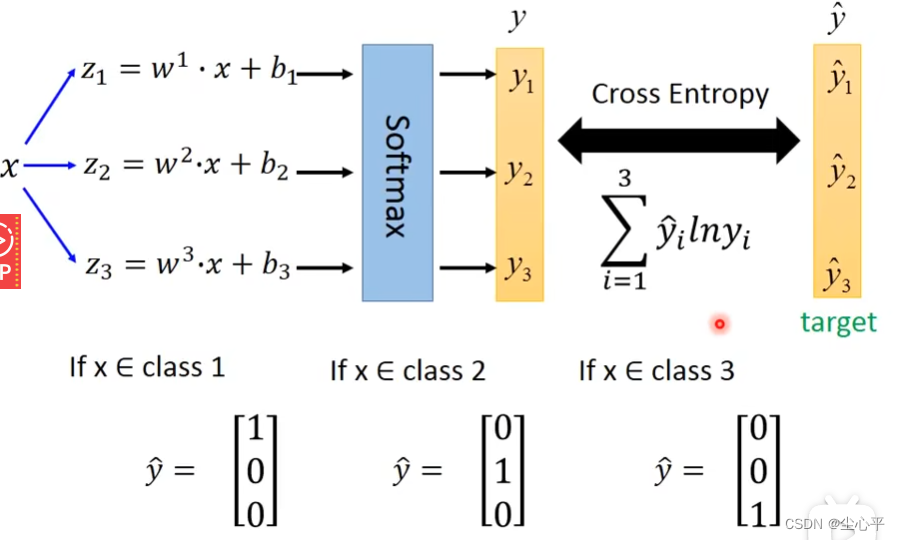
这样,三步骤就变为下图.注意样本特征的定义,样本属于哪个类别则对应的特征向量当前值为1其余均为0
输入特征处理→深度学习
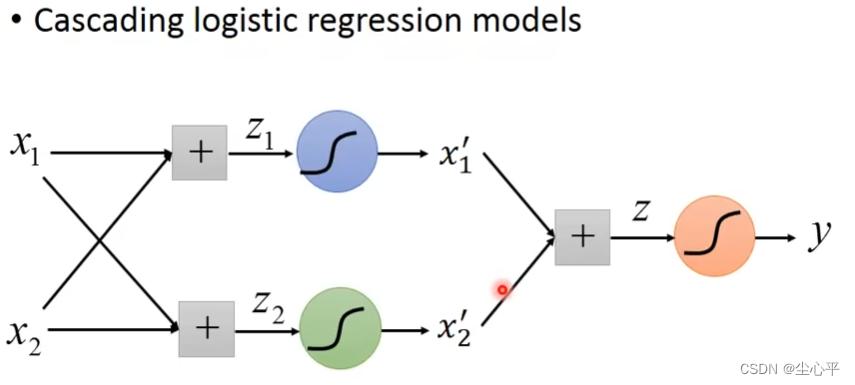
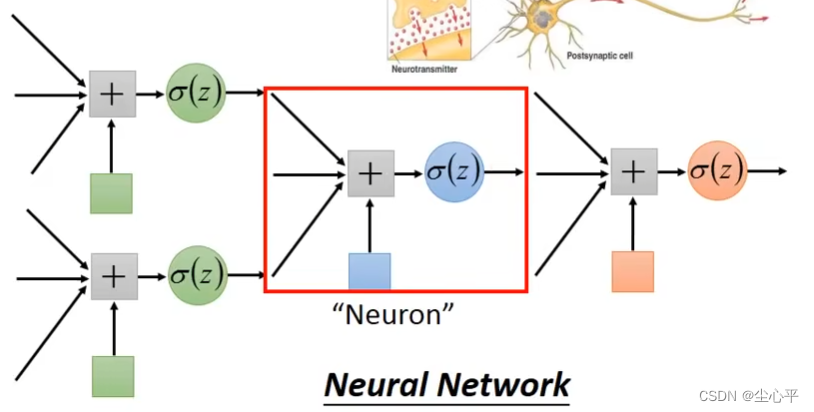
可能会有一些输入特征难以用一条直线去划分类别,这时我们就需要对输入特征做一些处理,这个处理在深度学习中即叫做隐含层。通过加入多层的sigmoid隐含层(多个逻辑回归)处理,使得输入值变为0~1之间,最后再用一个sofmax层输出即可得到正确的输出向量。此时这个网络就叫做神经网络,也就叫做深度学习
交叉熵的loss函数 当为二分类时,交叉熵loss函数的公式是: l o s s = − ∑ i n [ y ′ i l n y i + ( 1 − y ′ i ) ( 1 − l n y i ) ] loss=-\sum _i ^n [y^{'i}lny^i+(1-y^{'i})(1-lny^i)] loss=−i∑n[y′ilnyi+(1−y′i)(1−lnyi)] 当为多分类时,交叉熵loss函数的公式是: C ( y , y ′ ) = − ∑ i = 1 n ( y ′ i l n y i ) , n 为共多少个类别且 n > 2 C(y,y')=- \sum _{i=1} ^n(y'^ilny^i),n为共多少个类别且n>2 C(y,y′)=−i=1∑n(y′ilnyi),n为共多少个类别且n>2




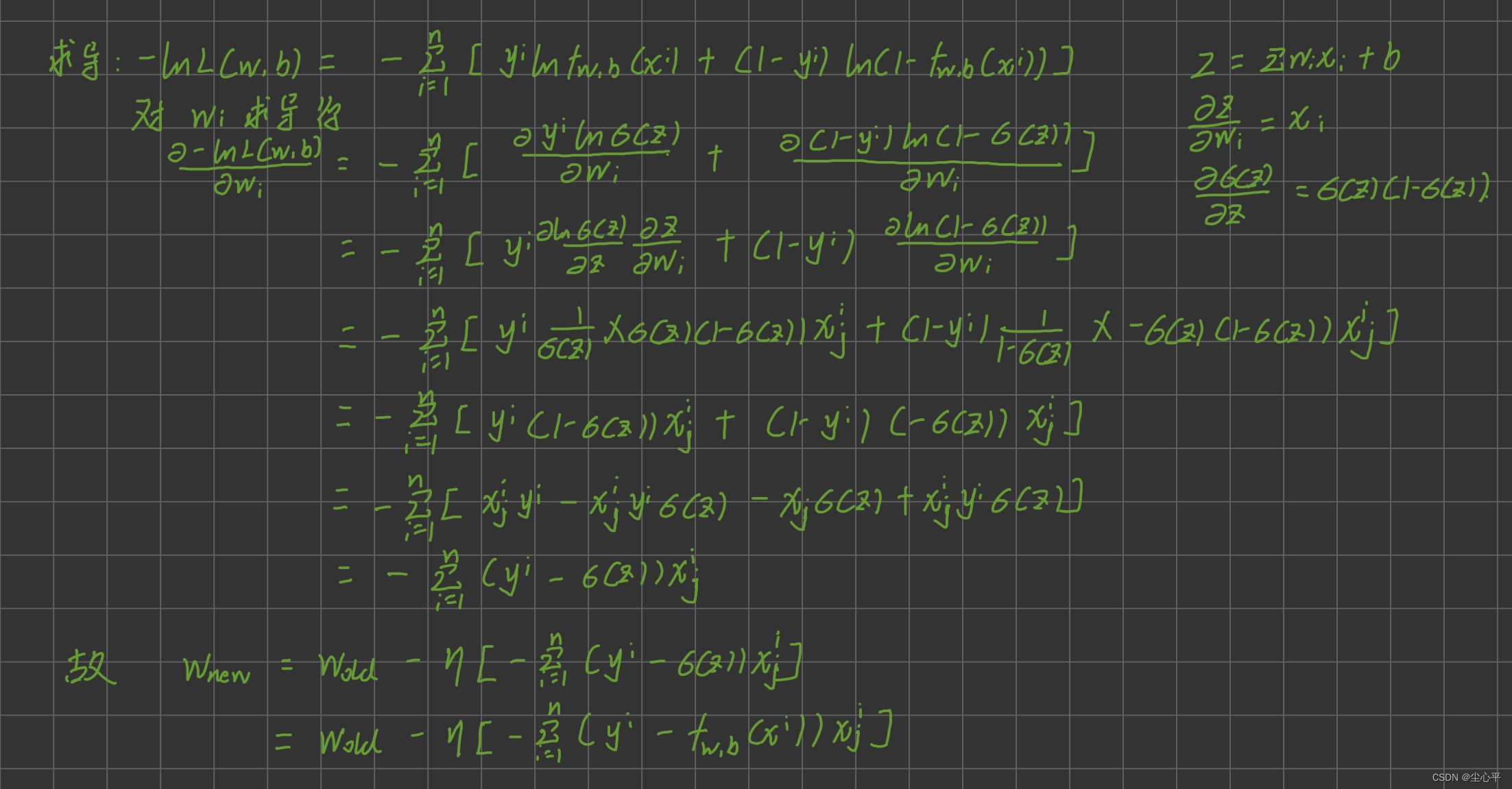
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fG1Z41IR-1671293558020)(image/image_sj9MN0smfA.png)]](https://img-blog.csdnimg.cn/232afbdc898744298eae9fc59deb89b9.png)



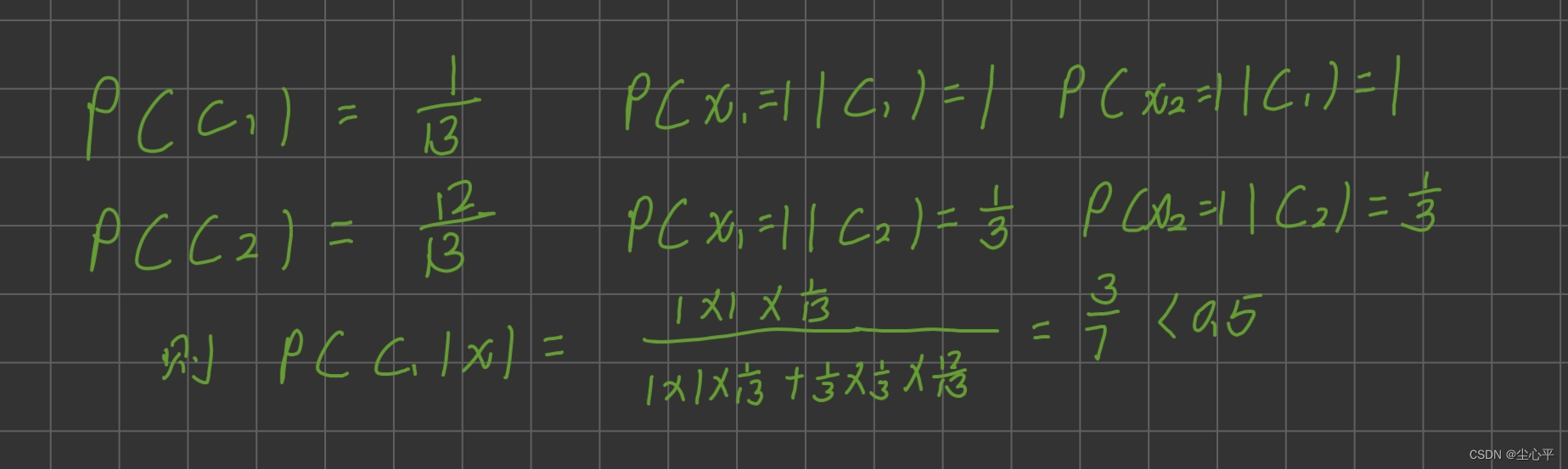










![行为树 --- [7] BehaviorTree.CPP 4.x版本的编译及使用](https://img-blog.csdnimg.cn/d48351ae319b4135b20b789b3cd827b5.png)