一【题目类别】

二【题目难度】

困难

三【题目编号】

968.监控二叉树

四【题目描述】

给定一个二叉树，我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。

五【题目示例】

示例 1：
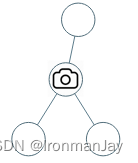
- 输入：[0,0,null,0,0]
- 输出：1
  - 解释：如图所示，一台摄像头足以监控所有节点。
示例 2：
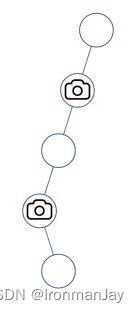
- 输入：[0,0,null,0,null,0,null,null,0]
- 输出：2
  - 解释：需要至少两个摄像头来监视树的所有节点。上图显示了摄像头放置的有效位置之一。

六【解题思路】

通过理解题意可以发现，任意一个节点只有三种情况（用数字对应每一种情况）：
- 1：当前节点有摄像头
- 2：当前节点没有摄像头，但是可以观察到
- 3：当前节点没有摄像头，并且不可以被观察到
利用这三种情况来判断是否可以给当前节点赋“摄像头”
还需要注意，如果要达到最小的“摄像头”数量，叶子节点肯定不能放摄像头，否则数量不是最小
还需要注意要从下向上遍历整棵树，因为要从叶子节点开始判断，所以使用后序遍历，在遍历的过程中可能有以下几种情况：
- 如果当前节点为空，说明遍历到分支了，也就是叶子节点，默认叶子节点可以被观察到，但是不能赋“摄像头”，那么返回2
- 如果当前节点的左右子节点有一个为3，说明当前节点要赋“摄像头”，“摄像头”数量加一，并且返回1
- 如果当前节点的左右子节点有一个为1，说明当前节点可以被观察到，所以返回2
- 其余的情况说明当前节点的左右子节点都没有摄像头，但是可以被观察到，那么当前节点不能赋“摄像头”，否则就不是最小数量了，返回3，表示需要一个“摄像头"来处理此节点，等待其余的遍历步骤处理
- 最后还要判断一下根节点是否需要赋“摄像头”，因为是从下向上遍历二叉树
最后返回结果即可

七【题目提示】

$给定树的节点数的范围是 [1, 1000] 。$
$每个节点的值都是 0 。$

八【时间频度】

时间复杂度： $O (n)$ ，其中 $n$ 为树的节点个数
空间复杂度： $O (1)$

九【代码实现】

Java语言版

class Solution {

    int res = 0;

    public int minCameraCover(TreeNode root) {
        if(getRes(root) == 3){
            res++;
        }
        return res;
    }

    public int getRes(TreeNode root){
        if(root == null){
            return 2;
        }
        int left = getRes(root.left);
        int right = getRes(root.right);
        if(left == 3 || right == 3){
            res++;
            return 1;
        }
        if(left == 1 || right == 1){
            return 2;
        }
        return 3;
    }

}

C语言版

int getRes(struct TreeNode* root,int* res)
{
    if(root == NULL)
    {
        return 2;
    }
    int left = getRes(root->left,res);
    int right = getRes(root->right,res);
    if(left == 3 || right == 3)
    {
        (*res)++;
        return 1;
    }
    if(left == 1 || right == 1)
    {
        return 2;
    }
    return 3;
}

int minCameraCover(struct TreeNode* root)
{
    int res = 0;
    if(getRes(root,&res) == 3)
    {
        res++;
    }
    return res;
}