文章目录

一：图像编码基本理论
- （1）图像压缩的必要性
- （2）图像压缩的可能性
- - A：编码冗余
  - B：像素间冗余
  - C：心理视觉冗余
- （3）图像压缩方法分类
- - A：基于编码前后的信息保持程度的分类
  - B：基于编码方法的分类
  - C：其他方法
- （4）图像编码术语
二：图像的无损压缩编码
- （1）无损编码理论
- （2）霍夫曼编码
- - A：概述
  - B：程序
- （3）算数编码
- - A：概述
  - B：程序
- （4）LZW编码
- - A：概述
  - B：程序

一：图像编码基本理论

图像编码：一种将数字图像转换为压缩表示形式的过程。它的目标是减少图像数据的存储空间，并在传输或存储时减少带宽和存储需求、主要分为两类

无损压缩：尽可能地保留原始图像的所有信息，以实现无失真的压缩。其中最常见的算法之一是无损JPEG（JPEG-LS）编码，它使用类似于有损JPEG的离散余弦变换，但保留了所有细节
有损压缩：通过牺牲一些细节和图像质量来实现更高的压缩比。最常见的有损压缩算法之一是JPEG（Joint Photographic Experts Group）编码。JPEG使用离散余弦变换（DCT）将图像分成不同频率的频谱，并根据人眼对颜色和亮度的感知特性来降低高频细节。这样可以大幅减少图像的体积，但会引入一定程度的失真

（1）图像压缩的必要性

图像压缩的必要性：

存储空间的节省：原始数字图像通常占据大量的存储空间。通过压缩图像，可以有效地减少其所占用的存储空间。例如，一个高分辨率的彩色图像可能需要几百兆字节的存储空间，而通过压缩可以将其缩小到几十兆字节或更少
传输效率的提高：对于需要通过网络进行传输的图像，较大的图像文件会占用更多的带宽和传输时间。通过压缩图像，可以显著降低传输所需的带宽和时间成本。这对于在线图片分享、视频流媒体等应用非常重要
资源的优化利用：在诸如移动设备、无人机、监控摄像头等资源受限的环境中，压缩图像可以减少处理和传输所需的计算资源和能源消耗。这有助于延长设备的电池寿命、提高处理速度，并降低硬件成本

例如，一部90分钟的彩色电影，每秒放映24帧。把它数字化，每帧512´512像素，每像素的R、G、B三分量分别占8b，则总比特数为

$90 \times 60 \times 24 \times 3 \times 512 \times 512 \times 8 bi t = 97, 200 MB$

因此，传输带宽、速度、存储器容量的限制使得对图象数据进行压缩显得非常必要

在这里插入图片描述

（2）图像压缩的可能性

A：编码冗余

编码冗余：称为信息熵冗余。如果一个图像的灰度级编码，使用了多于实际需要的编码符号，就称该图像包含了编码冗余\

例如下图，如果用8bit表示该图像的像素，那么则认为该图像存在编码冗余。因为该图像的像素只有两个灰度级，用1bit即可表示

在这里插入图片描述

在大多数图像中，图像像素的灰度值分布是不均匀的，因此若对图像的灰度值直接进行自然二进制编码（等长编码），则会对有最大和最小概率可能性的值分配相同比特数，而产生了编码冗余

在这里插入图片描述

用自然二进制编码时没有考虑像素灰度值出现的概率。只有按概率分配编码长度，才是最精减的编码方法。也即，灰度级出现概率大的用短码表示，出现概率小的灰度级用长码表示，则有可能使编码总长度下降

在这里插入图片描述

B：像素间冗余

像素间冗余：对应图像目标的像素之间一般具有相关性。因此，图像中一般存在与像素间相关性直接联系着的数据冗余——像素相关冗余。主要有

空间冗余：邻近像素灰度分布的相关性很强
频间冗余：多谱段图像中各谱段图像对应像素之间灰度相关性很强
时间冗余：序列图像帧间画面对应像素灰度的相关性很强
结构冗余：有些图像存在较强的纹理结构或自相似性，如墙纸、草席等图像
知识冗余：有些图像中包含与某些先验知识相关的信息

在这里插入图片描述

C：心理视觉冗余

心理视觉冗余：人的眼睛并不是对所有信息都有相同的敏感度，有些信息在通常的视觉感觉过程中与另外一些信息相比来说并不那么重要，这些信息可以认为是心理视觉冗余的

（3）图像压缩方法分类

A：基于编码前后的信息保持程度的分类

信息保持编码（无损编码）： 在编解码过程中保证图像信息不丢失，通常压缩比一般不超过3:1
保真度编码（有损编码）： 丢掉一些人眼不敏感的次要信息，在一定保真度准则下，最大限度地压缩图像
特征提取： 在图像识别、分析和分类等技术中，只对感兴趣部分特征进行编码压缩

B：基于编码方法的分类

熵编码： 基于信息统计特性的编码技术。如行程编码、Huffman编码和算术编码等
预测编码： 常用的有差分脉冲编码调制和运动估计与补偿预测编码法
变换编码： 将空间域图像经过正交变换映射到另一变换域上，再采用适当的量化和熵编码来有效压缩图像。通常采用的变换：离散傅里叶变换（DFT）、离散余弦变换（DCT）和离散小波变换（DWT）等

C：其他方法

早起编码方法：如混合编码、矢量量化、LZW算法等
一些新的编码方法
- 人工神经元网络ANN的压缩编码
- 分形编码
- 小波编码
- 基于模型的压缩编码
- 基于对象的压缩编码
- …

（4）图像编码术语

压缩比：

$r=\frac{n}{\bar{L}}=\frac{\text { 压缩前每像素所占平均比特数目 }}{\text { 压后每像素所占平均比特数目 }}$

图像熵：

令 $p(d_{i})$ 为数字图像第 $i$ 个灰度级 $d_{i}$ 的出现概率

$H=-\sum_{i=1}^{m} p\left(d_{i}\right) \log _{2} p\left(d_{i}\right)\left(p^{p i x e l} /{ }_{b i t}\right)$

平均码字长度 $\bar{L}$ ：

令 $L_{i}$ 为数字图像第 $i$ 个灰度级 $d_{i}$ 的编码长度

$\bar{L}=\sum_{i=1}^{m} L_{i} p\left(d_{i}\right) \quad(\text { pixel } / \text { bit })$

编码效率：

$\eta=\frac{H}{\bar{L}} \times 100 \%$

二：图像的无损压缩编码

（1）无损编码理论

Shannon无失真编码定理：也称为香农编码定理（Shannon’s source coding theorem），是信息论中的一个重要定理，由克劳德·香农（Claude Shannon）在1948年提出。该定理表明，在一给定离散概率分布下，对于任意平均码长小于熵的正数值，存在一种编码方式可以使得编码后的数据长度趋近于此平均码长，并且解码时不会引入任何失真。简而言之，香农无失真编码定理表明，对于具有确定概率分布的离散信源，我们可以设计一种编码方案，使得编码后的数据尽可能地紧凑，接近其熵值。在解码时，我们可以完全恢复原始的消息，没有任何信息的丢失或失真。这个定理在信息压缩领域具有重要的应用价值，它提供了一种理论基础和算法思路，用于有效地压缩数据并在解压缩时还原原始信息。同时，无失真编码定理也为其他信息论相关的研究和应用提供了重要参考和指导

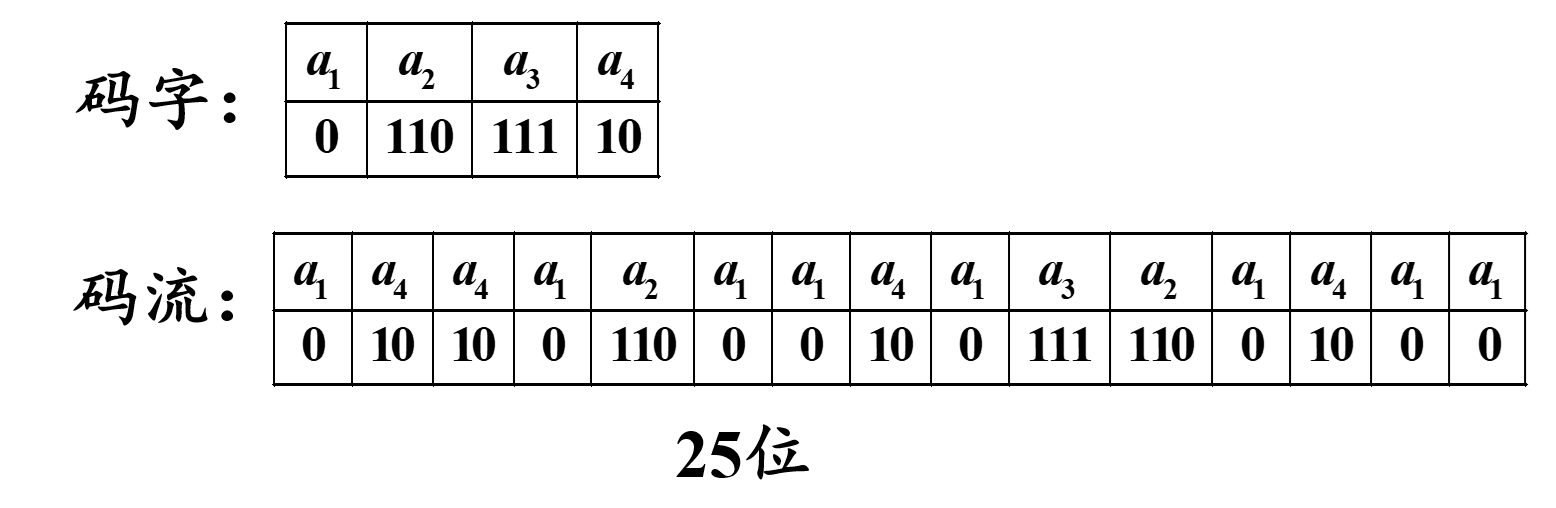
如下，假设有一原始符号序列为

$a_{1}a_{4}a_{4}a_{1}a_{2}a_{1}a_{1}a_{4}a_{1}a_{3}a_{2}a_{1}a_{4}a_{1}a_{1}$

若采用等长编码，等长编码是将所有符号当作等概率事件处理的

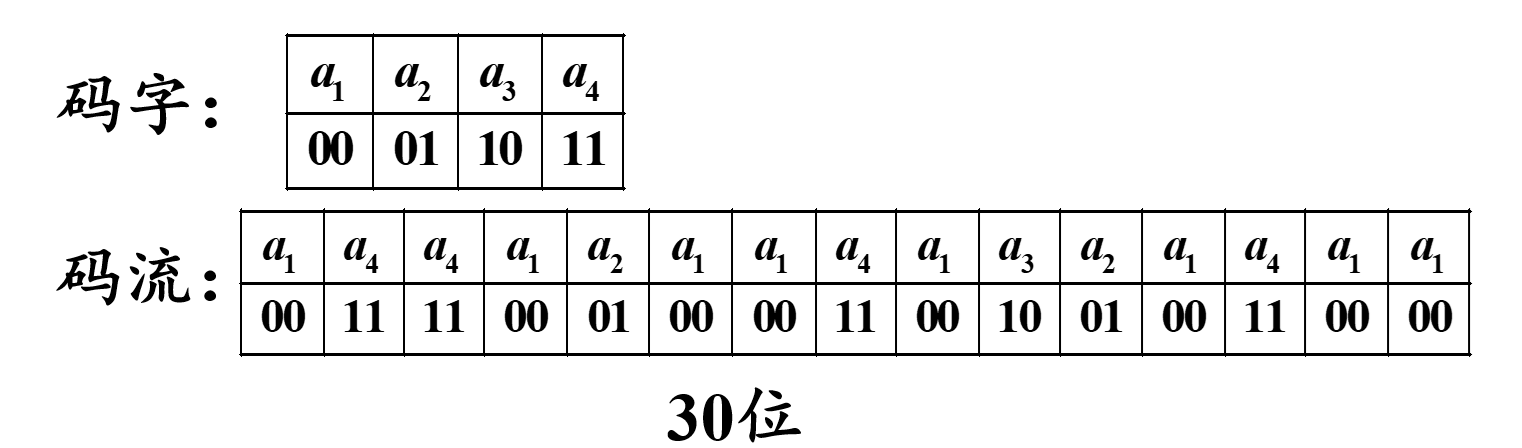
在这里插入图片描述

若采用变字长编码，变字长编码是每个符号的码字长度随字符出现概率而变化

$a_{1}$ ：8次
$a_{2}$ ：2次
$a_{3}$ ：1次
$a_{4}$ ：4次

在这里插入图片描述

（2）霍夫曼编码

A：概述

此部分内容不在详细介绍，请移步(王道408考研数据结构)第五章树-第四节3：哈夫曼树基本概念、构造和哈夫曼编码

B：程序

实现图像的霍夫曼编码

matlab：

clc;clear;
%load image
Image=[7 2 5 1 4 7 5 0; 5 7 7 7 7 6 7 7; 2 7 7 5 7 7 5 4; 5 2 4 7 3 2 7 5;
       1 7 6 5 7 6 7 2; 3 3 7 3 5 7 4 1; 7 2 1 7 3 3 7 5; 0 3 7 5 7 2 7 4];
[h w]=size(Image);   totalpixelnum=h*w;
len=max(Image(:))+1;
for graynum=1:len
    gray(graynum,1)=graynum-1;%将图像的灰度级统计在数组gray第一列
end
%将各个灰度出现的频数统计在数组histgram中
for graynum=1:len
    histgram(graynum)=0;    gray(graynum,2)=0;
    for i=1:w
        for j=1:h
            if gray(graynum,1)==Image(j,i)
                histgram(graynum)=histgram(graynum)+1;
            end
        end
    end
    histgram(graynum)=histgram(graynum)/totalpixelnum;
end
histbackup=histgram;
%找到概率序列中最小的两个，相加，依次增加数组hist的维数，存放每一次的概率和，同时将原概率屏蔽（置为1.1）；
%最小概率的序号存放在tree第一列中，次小的放在第二列
sum=0;     treeindex=1;
while(1)
    if sum>=1.0
        break;
    else
        [sum1,p1]=min(histgram(1:len));   histgram(p1)=1.1;
        [sum2,p2]=min(histgram(1:len));   histgram(p2)=1.1;
        sum=sum1+sum2;                len=len+1;          histgram(len)=sum;
        tree(treeindex,1)=p1;         tree(treeindex,2)=p2;
        treeindex=treeindex+1;        
    end
end
%数组gray第一列表示灰度值，第二列表示编码码值，第三列表示编码的位数
for k=1:treeindex-1
    i=k;    codevalue=1;
    if or(tree(k,1)<=graynum,tree(k,2)<=graynum)
        if tree(k,1)<=graynum
            gray(tree(k,1),2)=gray(tree(k,1),2)+codevalue;
            codelength=1;
            while(i<treeindex-1)
                codevalue=codevalue*2;
                for j=i:treeindex-1
                    if tree(j,1)==i+graynum
                        gray(tree(k,1),2)=gray(tree(k,1),2)+codevalue;
                        codelength=codelength+1;
                        i=j;      break;
                    elseif tree(j,2)==i+graynum
                        codelength=codelength+1;
                        i=j;      break;
                    end
                end
            end
            gray(tree(k,1),3)=codelength;
        end
        i=k;    codevalue=1;
        if tree(k,2)<=graynum
            codelength=1;
            while(i<treeindex-1)
                codevalue=codevalue*2;
                for j=i:treeindex-1
                    if tree(j,1)==i+graynum
                        gray(tree(k,2),2)=gray(tree(k,2),2)+codevalue;
                        codelength=codelength+1;
                        i=j;      break;
                    elseif tree(j,2)==i+graynum
                        codelength=codelength+1;
                        i=j;   break;
                    end
                end
            end
            gray(tree(k,2),3)=codelength;
        end
    end
end
%把gray数组的第二三列，即灰度的编码值及编码位数输出
for k=1:graynum
    A{k}=dec2bin(gray(k,2),gray(k,3));
end
disp('编码');
disp(A);

python：

import numpy as np
import matplotlib.pyplot as plt

# Load image
Image = np.array([[7, 2, 5, 1, 4, 7, 5, 0],
                  [5, 7, 7, 7, 7, 6, 7, 7],
                  [2, 7, 7, 5, 7, 7, 5, 4],
                  [5, 2, 4, 7, 3, 2, 7, 5],
                  [1, 7, 6, 5, 7, 6, 7, 2],
                  [3, 3, 7, 3, 5, 7, 4, 1],
                  [7, 2, 1, 7, 3, 3, 7, 5],
                  [0, 3, 7, 5, 7, 2, 7, 4]])

h, w = Image.shape
totalpixelnum = h * w
len = np.max(Image) + 1

gray = np.zeros((len, 3))
gray[:, 0] = np.arange(len)

histgram = np.zeros(len)
for graynum in range(len):
    histgram[graynum] = np.sum(Image == graynum) / totalpixelnum

histbackup = histgram.copy()

sum_val = 0
treeindex = 0
tree = np.zeros((len, 2))
while True:
    if sum_val >= 1.0:
        break
    else:
        p1 = np.argmin(histgram)
        histgram[p1] = 1.1
        p2 = np.argmin(histgram)
        histgram[p2] = 1.1
        sum_val = histbackup[p1] + histbackup[p2]
        len += 1
        histgram[len-1] = sum_val
        tree[treeindex, 0] = p1
        tree[treeindex, 1] = p2
        treeindex += 1

gray[:, 1] = np.arange(len)

for k in range(treeindex):
    i = k
    codevalue = 1
    if tree[k, 0] <= graynum or tree[k, 1] <= graynum:
        if tree[k, 0] <= graynum:
            gray[int(tree[k, 0]), 1] += codevalue
            codelength = 1
            while i < treeindex - 1:
                codevalue *= 2
                for j in range(i, treeindex - 1):
                    if tree[j, 0] == i + graynum:
                        gray[int(tree[k, 0]), 1] += codevalue
                        codelength += 1
                        i = j
                        break
                    elif tree[j, 1] == i + graynum:
                        codelength += 1
                        i = j
                        break
            gray[int(tree[k, 0]), 2] = codelength

        i = k
        codevalue = 1
        if tree[k, 1] <= graynum:
            codelength = 1
            while i < treeindex - 1:
                codevalue *= 2
                for j in range(i, treeindex - 1):
                    if tree[j, 0] == i + graynum:
                        gray[int(tree[k, 1]), 1] += codevalue
                        codelength += 1
                        i = j
                        break
                    elif tree[j, 1] == i + graynum:
                        codelength += 1
                        i = j
                        break
            gray[int(tree[k, 1]), 2] = codelength

# Convert gray code to binary strings
A = [bin(int(x[1]))[2:].zfill(int(x[2])) for x in gray[:len]]

# Display the encoding
print("编码:")
for i, code in enumerate(A):
    print(f"{i}: {code}")

# Plotting the image
plt.imshow(Image, cmap='gray')
plt.axis('off')
plt.show()

（3）算数编码

A：概述

算数编码：是一种无失真的数据压缩技术，用于将源数据序列转换为更紧凑的编码序列。与传统的固定长度编码方法（如霍夫曼编码）不同，算术编码使用一个区间来表示整个源数据序列，而不是将每个符号映射到固定长度的编码字。算术编码的基本思想是利用符号出现的概率分布来为每个符号分配一个对应的区间，并根据输入的符号序列逐步缩小区间范围。最终，所生成的区间内的任意一个数值都可以表示原始数据序列的唯一编码。基本步骤如下

初始化：给定待编码的符号序列和对应的概率分布。
创建初始区间：根据符号的概率分布，为每个符号分配一个区间。
编码：根据每个输入符号，按照其在当前区间的长度比例，更新区间的上界和下界。
重标定：根据区间的更新，进行重标定以保证精度和避免溢出。
输出：当所有符号编码完成后，输出最终区间中的任意一个编码值作为压缩结果

算术编码的优势在于可以实现接近熵编码效率的压缩比，尤其适用于符号概率分布不均匀、频率较高的数据。然而，算术编码的实现相对复杂且计算量大，同时对解码过程中的精度要求较高。需要注意的是，由于算术编码涉及到浮点数运算和精度处理，因此在实际应用中可能存在一定的误差累积和舍入误差问题。这些问题可以通过使用更高精度的数值表示或采用其他技巧来缓解。总之，算术编码是一种强大的数据压缩技术，能够提供较高的压缩比，尤其适用于无损压缩和对压缩比要求较高的场景

B：程序

matlab：

%算术编码
clc;clear;
%load image
%Image=[7 2 5 1 4 7 5 0;5 7 7 7 7 6 7 7;2 7 7 5 7 7 5 4;5 2 4 7 3 2 7 5;
%       1 7 6 5 7 6 7 2;3 3 7 3 5 7 4 1;7 2 1 7 3 3 7 5;0 3 7 5 7 2 7 4];
Image=[4 1 3 1 2];   
[h w col]=size(Image);   pixelnum=h*w;
graynum=max(Image(:))+1;
for i=1:graynum
    gray(i)=i-1;
end
histgram=zeros(1,graynum);
for i=1:w
    for j=1:h
        pixel=uint8(Image(j,i)+1);
        histgram(pixel)=histgram(pixel)+1;          
    end    
end
histgram=histgram/pixelnum;%将各个灰度出现的频数统计在数组histgram中
disp('灰度级');disp(num2str(gray));
disp('概率');disp(num2str(histgram))
disp('每一行字符串及其左右编码：')
for j=1:h
    str=num2str(Image(j,:));    left=0;    right=0;
    intervallen=1;              len=length(str);
    for i=1:len
        if str(i)==' '
            continue;
        end
        m=str2num(str(i))+1;      pl=0;        pr=0;
        for j=1:m-1
            pl=pl+histgram(j);
        end
        for j=1:m
            pr=pr+histgram(j);
        end
        right=left+intervallen*pr; left=left+intervallen*pl;%间隔区间起始和终止端点           
        intervallen=right-left; %  间隔区间宽度     
    end
    %输入图像信息数据
    disp(str);  
    %编码输出间隔区间
    disp(num2str(left));  disp(num2str(right))    
    temp=0;  a=1;
    while(1)
        left=2*left;
        right=2*right;
    if floor(left)~=floor(right)
        break;
    end
    temp=temp+floor(left)*2^(-a);
    a=a+1;
    left=left-floor(left);
    right=right-floor(right);
    end
    temp=temp+2^(-a);
    ll=a;
    %寻找最后区间内的最短二进制小数和所需的比特位数
    disp(num2str(temp));  disp(ll);    
    %算术编码的编码码字输出：
    disp('算术编码的编码码字输出：'); 
    %yy=DEC2bin(temp,ll);
    %简单的将10进制转化为N为2进制小数
    for ii= 1: ll
        temp1=temp*2;
        yy(ii)=floor(temp1);
        temp=temp1-floor(temp1);
    end
    disp(num2str(yy));    
end

python：

import numpy as np

# 算术编码
# load image
Image = np.array([[4, 1, 3, 1, 2]])
[h, w] = Image.shape
pixelnum = h * w
graynum = np.max(Image) + 1

gray = np.arange(graynum)

histgram = np.zeros(graynum)
for i in range(w):
    for j in range(h):
        pixel = Image[j, i]
        histgram[pixel] += 1

histgram /= pixelnum
print('灰度级:', gray)
print('概率:', histgram)

print('每一行字符串及其左右编码：')
for j in range(h):
    str_ = [str(x) for x in Image[j]]
    left = 0
    right = 0
    intervallen = 1
    len_ = len(str_)
    for i in range(len_):
        if str_[i] == ' ':
            continue
        m = int(str_[i]) + 1
        pl = np.sum(histgram[:m-1])
        pr = np.sum(histgram[:m])
        right = left + intervallen * pr
        left = left + intervallen * pl
        intervallen = right - left
    
    print(''.join(str_))
    print(left, right)
    
    temp = 0
    a = 1
    while True:
        left *= 2
        right *= 2
        if int(left) != int(right):
            break
        temp += int(left) * pow(2, -a)
        a += 1
        left -= int(left)
        right -= int(right)
    
    temp += pow(2, -a)
    ll = a
    
    print(temp, ll)
    
    print('算术编码的编码码字输出：')
    yy = []
    for ii in range(ll):
        temp1 = temp * 2
        yy.append(int(temp1))
        temp = temp1 - int(temp1)
    
    print(yy)

（4）LZW编码

A：概述

**LZW编码：是一种用于数据压缩的无损压缩算法，它可以将输入数据中的重复模式编码为更短的代码，从而减小数据的存储空间。LZW编码最初由Terry Welch在1984年提出，广泛应用于图像、音频和文本等领域。LZW编码的基本思想是利用字典来对输入数据进行编码。初始时，字典中包含所有可能的单个字符作为键，以及相应的编号作为值。然后，从输入数据的开头开始，逐步扫描输入数据，并检查当前扫描的序列是否已经在字典中存在。如果已存在，则继续向后扫描并将当前序列与下一个字符拼接，直到找到一个新的序列。此时，将该新序列的编号输出，并将这个新序列添加到字典中，以供后续的编码使用。整个过程持续进行，直到扫描完整个输入数据。LZW编码的关键是维护一个动态更新的字典。在编码过程中，字典不断增长，并根据输入数据中的模式进行更新。因此，相同的输入数据可以使用不同长度的编码表示，具有较高的压缩比

B：程序

matlab：

clc;clear;
Image=[30 30 30 30;110 110 110 110;
       30 30 30 30;110 110 110 110];
[h w col]=size(Image);
pixelnum=h*w;     graynum=256;
%graynum=max(Image(:))+1;
if col==1    
    graystring=reshape(Image',1,pixelnum);%灰度图像从二维变为一维信号
    for tablenum=1:graynum
        table{tablenum}=num2str(tablenum-1);
    end
    len=length(graystring);   lzwstring(1)=graynum;
    R='';         stringnum=1;
    for i=1:len
        S=num2str(graystring(i));
        RS=[R,S];      flag=ismember(RS,table);
        if flag
            R=RS;
        else
            lzwstring(stringnum)=find(cellfun(@(x)strcmp(x,R),table))-1;
            stringnum=stringnum+1;     tablenum=tablenum+1;
            table{tablenum}=RS;        R=S;
        end
    end
    lzwstring(stringnum)=find(cellfun(@(x)strcmp(x,R),table))-1;
    disp('LZW码串： ')
    disp(lzwstring)
end

python：

import numpy as np

Image = np.array([[30, 30, 30, 30],
                  [110, 110, 110, 110],
                  [30, 30, 30, 30],
                  [110, 110, 110, 110]])

[h, w] = Image.shape
pixelnum = h * w
graynum = 256

if Image.ndim == 2:
    graystring = Image.T.flatten()
    table = {str(i): i for i in range(graynum)}
    lzwstring = [graynum]
    R = ''
    stringnum = 1

    for i in range(len(graystring)):
        S = str(graystring[i])
        RS = R + S
        if RS in table:
            R = RS
        else:
            lzwstring.append(table[R])
            stringnum += 1
            tablenum = len(table)
            table[RS] = tablenum
            R = S

    lzwstring.append(table[R])
    print('LZW码串：')
    print(lzwstring)