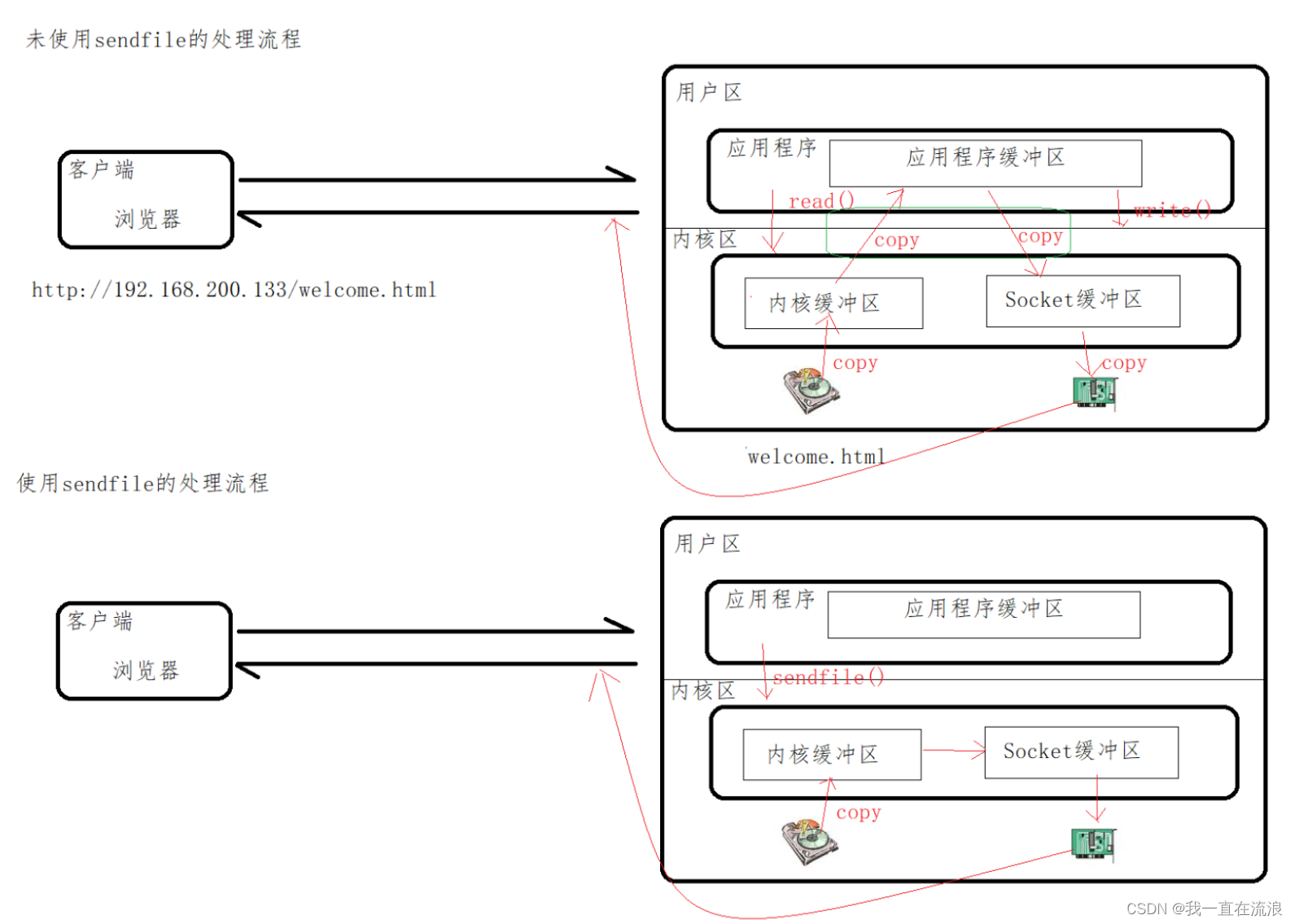
分段函数主要看在临界点处的左右极限是否相等,若相等则整段函数即为连续
(反之若是连续函数,在某一点为间断点,则可推导出一定为可去间断点)
无定义的点一定为间断点
如果该点有极限则为可去间断点




由于x的不确定导致了函数的不确定,要先补完函数再去求极限
(关键在于此处是n->+∞!!!可认为成未完成的函数)
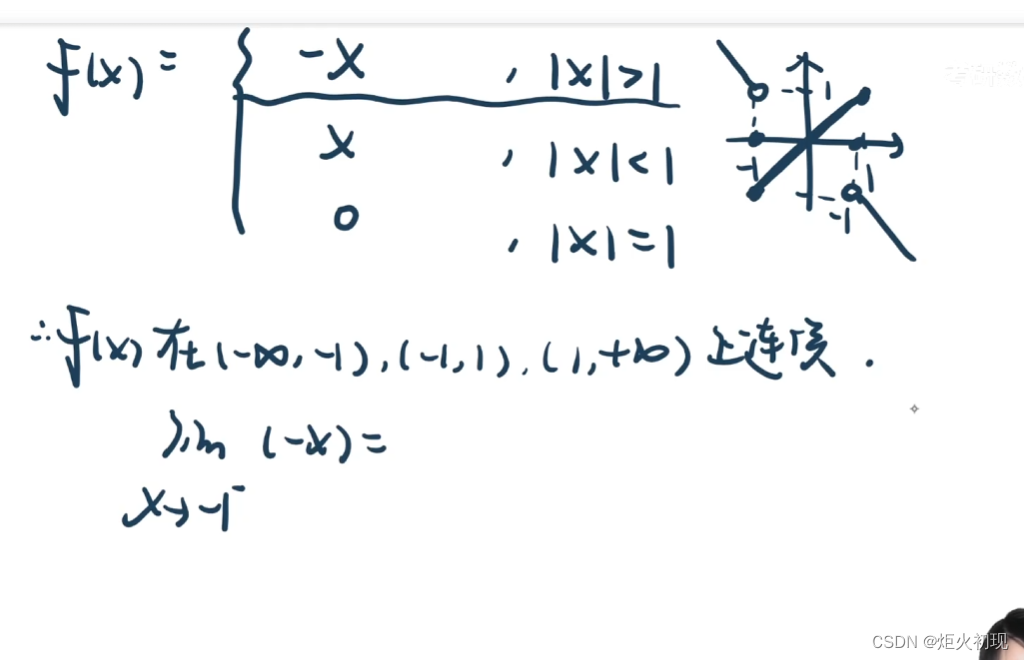

通过放缩使用夹逼定理得出

推3的时候就已经证明了1和2




局部保界性





任意取r0处,由于该函数可看作两个点列构成
故通过两个点列分别求极限,只有两个点列在该点均能有极限,且相等才能说明该点有极限

从cotΠ/2开始向0逼近会有很多不定义点出现,变成跳跃间断点
在此小段,再加上一段函数趋向于无穷以修复此问题


初等函数,定义域就是连续区间

关键在于max和min函数可以转化成右边的形式

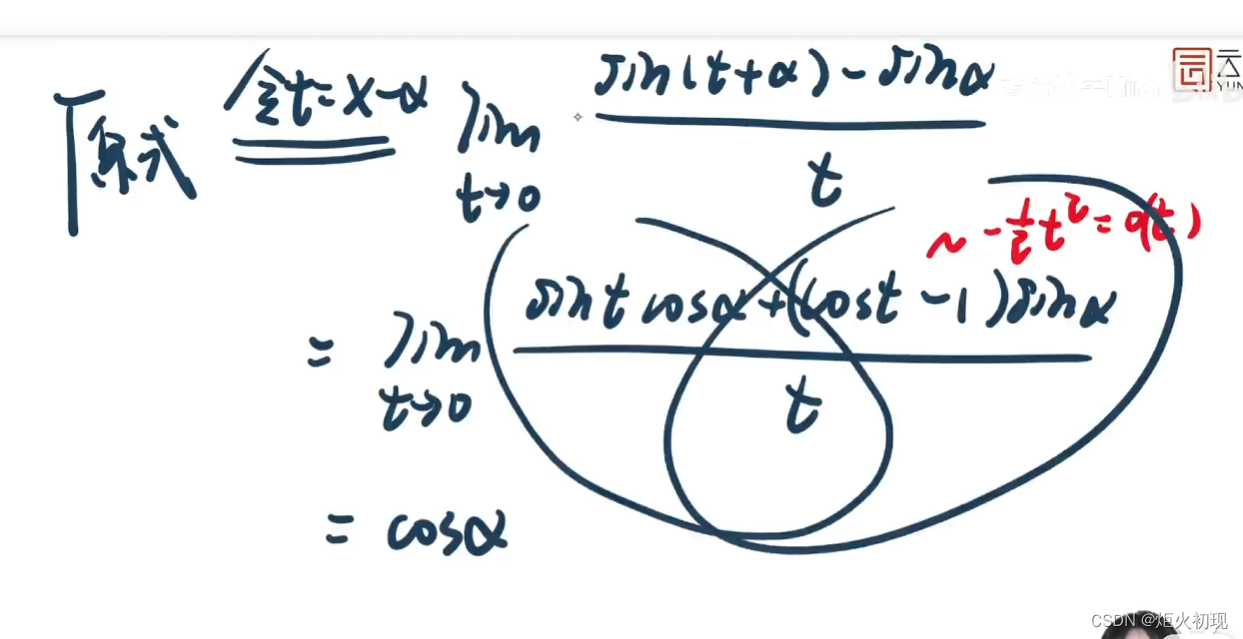
0/0型可以用代换的方式去替换无穷小的东西
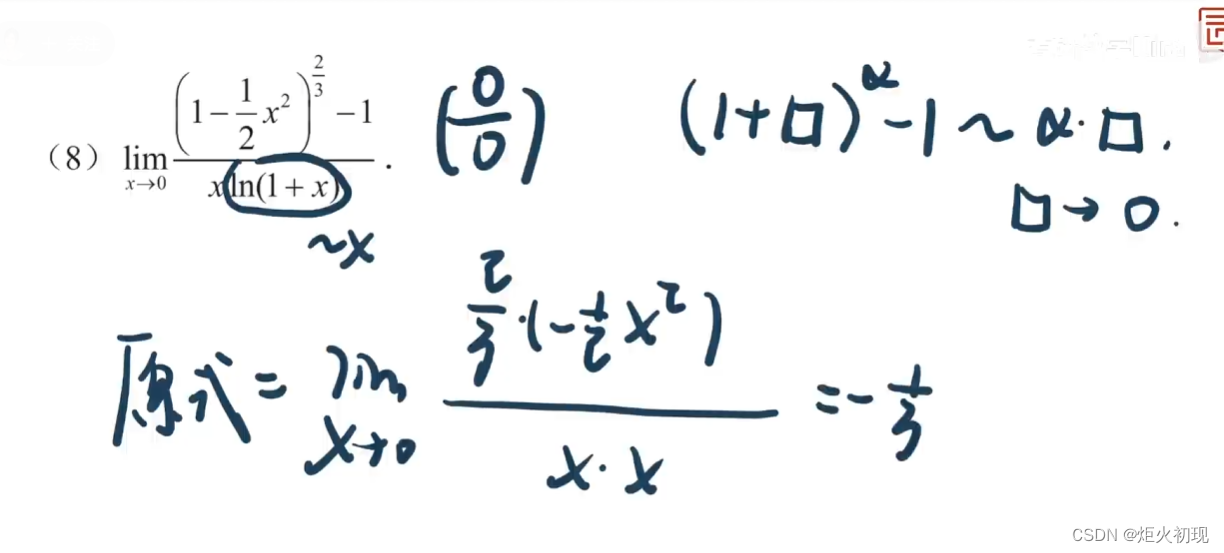
一般来说当分子分母为多个相乘的时候(或者只有一个)的时候常用等价无穷小

极限不为0的可以先代入

特殊的因式分解




先证明|x|>X时有界,那我们就反着来,先根据极限的定义必然有x>|x|时候,f(x)<1+|A|
(1是随便定的误差范围)
再去证明[-x,x]之间即可