题目描述：105. 从前序与中序遍历序列构造二叉树（中等）

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

LeetCode做题链接：LeetCode-从前序与中序遍历序列构造二叉树

示例 1：
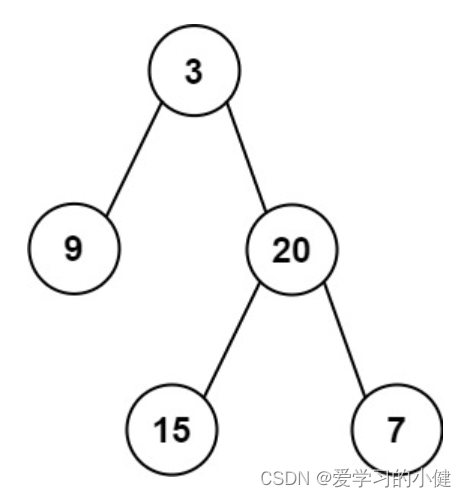
在这里插入图片描述

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2：

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示：

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

题目接口

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {

    }
}

解题思路

参考题解：动画演示 105. 从前序与中序遍历序列构造二叉树、

主要的思路是通过递归地将给定的preorder和inorder数组分成左右两半，并根据中序遍历的特点来构建二叉树。具体步骤如下：

从前序遍历的第一个元素开始，找到在中序遍历中的对应位置。
将中序遍历划分成左子树和右子树。
对左子树和右子树分别进行递归操作，构建它们的子树。
返回根节点。

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
		 if (preorder.length == 0 || inorder.length == 0) {
            return null;
        }
        // 根据前序数组的第一个元素，就可以确定根节点
        TreeNode root = new TreeNode(preorder[0]);
        for (int i = 0; i < preorder.length; ++i) {
            // 用preorder[0]去中序数组中查找对应的元素
            if (preorder[0] == inorder[i]) {
                // 将前序数组分成左右两半，再将中序数组分成左右两半
                // 之后递归的处理前序数组的左边部分和中序数组的左边部分
                // 递归处理前序数组右边部分和中序数组右边部分
                int[] pre_left = Arrays.copyOfRange(preorder, 1, i + 1);
                int[] pre_right = Arrays.copyOfRange(preorder, i + 1, preorder.length);
                int[] in_left = Arrays.copyOfRange(inorder, 0, i);
                int[] in_right = Arrays.copyOfRange(inorder, i + 1, inorder.length);
                root.left = buildTree(pre_left, in_left);
                root.right = buildTree(pre_right, in_right);
                break;
            }
        }
        return root;
    }
}