cluster:簇
原理:
这边暂时没有时间具体介绍kmeans聚类的原理。简单来说,就是首先初始化k个簇心;然后计算所有点到簇心的欧式距离,对一个点来说,距离最短就属于那个簇;然后更新不同簇的簇心(簇内所有点的平均值,也就是簇内点的重心);循环往复,直至簇心不变或达到规定的迭代次数
python实现
我们这边通过调用sklearn.cluster中的kmeans方法实现kmeans聚类
入门
原始数据的散点图
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
# 数据
class1 = 1.5 * np.random.randn(100,2) #100个2维点,标准差1.5正态分布
class2 = 1.5*np.random.randn(100,2) + np.array([5,5])#标准正态分布平移5,5
# 画出数据的散点图
plt.figure(0,dpi = 300)
plt.scatter(class1[:,0],class1[:,1],c='y',marker='*')
plt.scatter(class2[:,0],class2[:,1],c='k',marker='.')
plt.axis('off') # 不显示坐标轴
plt.show()

kmeans聚类
#---------------------------kmeans--------------------
# 调用kmeans函数
features = np.vstack((class1,class2))
kmeans = KMeans(n_clusters=2)
kmeans .fit(features)
plt.figure(1,dpi = 300)
#满足聚类标签条件的行
ndx = np.where(kmeans.labels_==0)
plt.scatter(features[ndx,0],features[ndx,1],c='b',marker='*')
ndx = np.where(kmeans.labels_==1)
plt.scatter(features[ndx,0],features[ndx,1],c='r',marker='.')
# 画出簇心
plt.scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],c='g',marker='o')
plt.axis('off') # 去除画布边框
plt.show()

进一步:选择簇心k的值
前面的数据是我们自己创建的,所以簇心k是我们自己可以定为2。但是在实际中,我们不了解数据,所以我们需要根据数据的情况确定最佳的簇心数k。
这是下面用到的数据data11_2.txt【免费】这是kmean聚类中用到的一个数据资源-CSDN文库
簇内离差平方方和与拐点法(不太好判断)
定义是簇内的点,
是簇的重心。
则所有簇的簇内离差平方和的和为。然后通过可视化的方法,找到拐点,认为突然变化的点就是寻找的目标点,因为继续随着k的增加,聚类效果没有大的变化
借助python中的“md = KMeans(i).fit(b),md.inertia_”实现。
import numpy as np
from sklearn.cluster import KMeans
import pylab as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
a = np.loadtxt('data/data11_2.txt') # 加载数
b=(a-a.min(axis=0))/(a.max(axis=0)-a.min(axis=0)) # 标准化
# 求出k对应的簇内离差平均和的和
SSE = []; K = range(2, len(a)+1)
for i in K:
md = KMeans(i).fit(b)
SSE.append(md.inertia_) # 它表示聚类结果的簇内平方误差和(Inertia)
# 可视化
plt.figure(1)
plt.title('k值与离差平方和的关系曲线')
plt.plot(K, SSE,'*-');
# 生成想要的 x 轴刻度细化值
x_ticks = np.arange(2, 10, 1)
# 设置 x 轴刻度
plt.xticks(x_ticks)
plt.show()
通过上图可以看出k=3时,是个拐点。所有选择k=3。
轮廓系数法(十分客观)
定义样本点i的轮廓系数,S_i代表样本点i的轮廓系数,a_i代表该点到簇内其他点的距离的均值;b_i分两步,首先计算该点到其他簇内点距离的平均距离,然后将最小值作为b_i。a_i表示了簇内的紧密度,b_i表示了簇间的分散度。
k个簇的总轮廓点系数定义为所有样本点轮廓系数的平均值。因此计算量大
总轮廓系数越接近1,聚类效果越好。簇内平均距离小,簇间平均距离大。
调用sklearn.metrics中的silhouette_score(轮廓分数)函数实现
#程序文件ex11_7.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
plt.rcParams['font.sans-serif'] = ['SimHei']
# 忽略警告
import warnings
# 使用过滤器来忽略特定类型的警告
warnings.filterwarnings("ignore")
a = np.loadtxt('data/data11_2.txt')
b=(a-a.min(axis=0))/(a.max(axis=0)-a.min(axis=0))
S = []; K = range(2, len(a))
for i in K:
md = KMeans(i).fit(b)
labels = md.labels_
S.append(silhouette_score(b, labels))
plt.figure(dpi = 300)
plt.title('k值与轮廓系数的关系曲线')
plt.plot(K, S,'*-'); plt.show()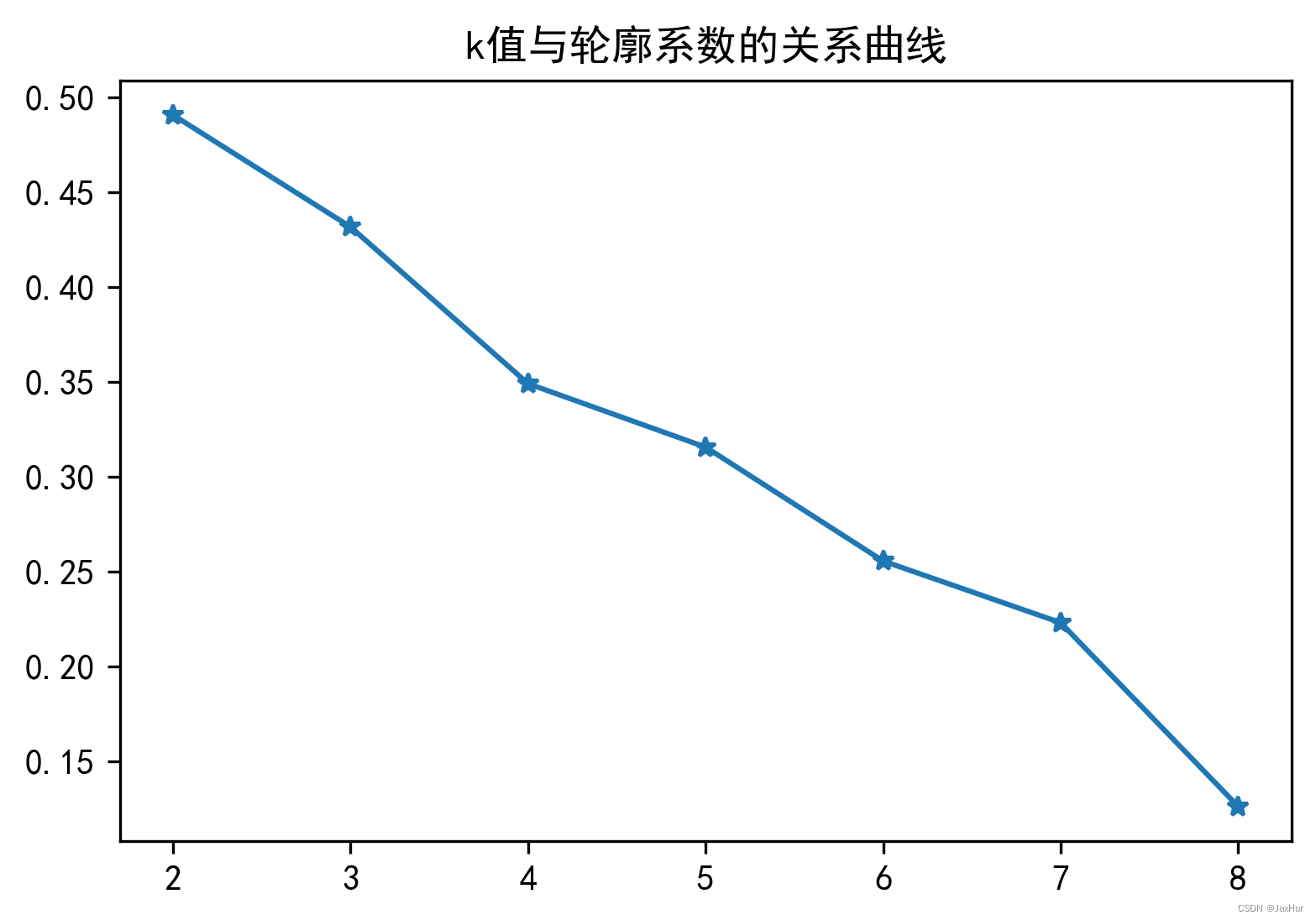
综上两种方法,好像并没有什么最好的方法,离差平均和不好判断,轮廓系数又像上面的情况。感觉综合两种方法比较好