目录

  1.算法实现步骤

  2.算法核心代码

  3.算法效果展示

---

  1.算法实现步骤

#二维插值函数的展示通过Axes3D函数来进行实现
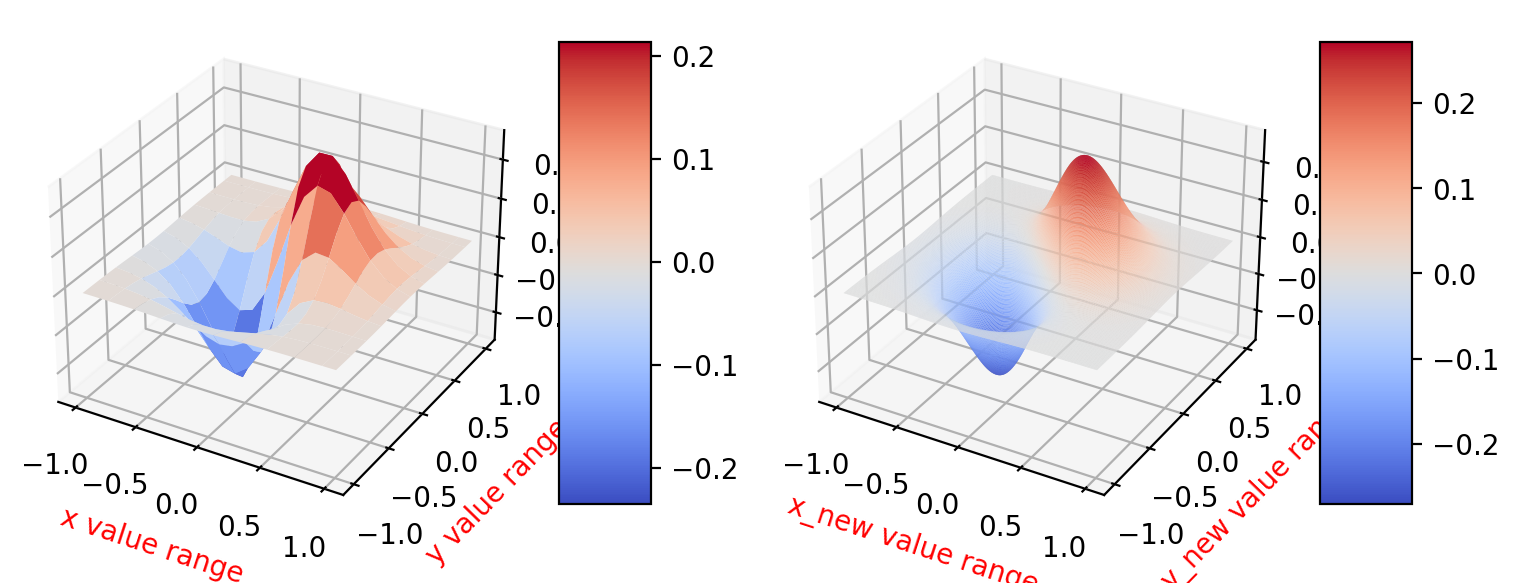
#我们需要绘制出20*20的插值效果和500*500的插值效果,进行比较.
具体步骤如下所示:
1.将x-y分为20*20并且绘制网格图
2.进行20*20的插值计算并且绘制可视化图片
3.将x-y分为500*500并且绘制网格图
4.进行500*500的插值计算并且绘制可视化图片
5.进行对比分析插值程度对于函数的影响
结论:我们最终发现插值程度越大,函数绘制越细腻,综合效果更好.

  2.算法核心代码

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt

#定义模型函数
def test_fun(x, y):
    return (x+y)*np.exp(-5.0*(x*x + y*y))

#第一张图片
# X-Y轴分为20*20的网格,计算20x20的二维插值
x = np.linspace(-1, 1, 20)
y = np.linspace(-1,1,20)
x, y = np.meshgrid(x, y)

fvals = test_fun(x,y) # 计算每个网格点上的函数值  15*15的值

fig = plt.figure(figsize=(9, 6))

ax=plt.subplot(1, 2, 1,projection = '3d')
surf = ax.plot_surface(x, y, fvals, color='r',rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax.set_xlabel('x value range',color='r')
ax.set_ylabel('y value range',color='r')
ax.set_zlabel('f(x, y)',color='r')
plt.colorbar(surf, shrink=0.5, aspect=5)

#第二张图片
#利用三阶样条插值法
new_test_fun= interpolate.interp2d(x, y, fvals, kind='cubic')
#计算500x500网格上的插值函数
x1 = np.linspace(-1, 1, 500)
y1 = np.linspace(-1,1,500)
fvals_new = new_test_fun(x1,y1)
x1,y1=np.meshgrid(x1, y1)
ax2=plt.subplot(1,2,2,projection = '3d')
surf_new = ax2.plot_surface(x1, y1, fvals_new, color='r',rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax2.set_xlabel('x_new value range',color='r')
ax2.set_ylabel('y_new value range',color='r')
ax2.set_zlabel('new_f(x, y)',color='r')
plt.colorbar(surf_new, shrink=0.5, aspect=5)
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/二维插值模型.png', dpi=200, bbox_inches='tight')
plt.show()

  3.算法效果展示