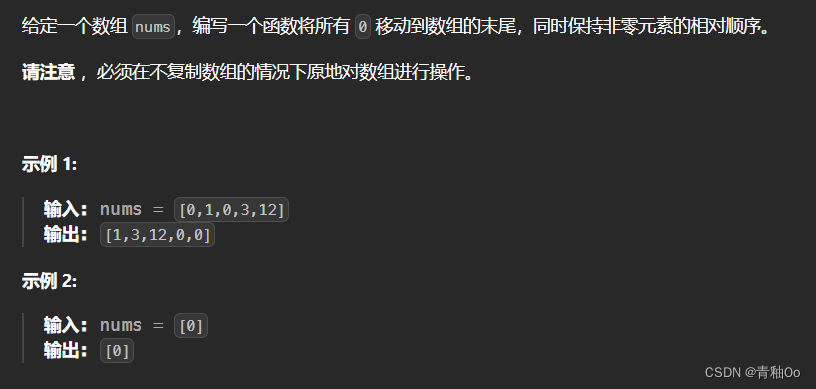
435. 无重叠区间 (需要二刷)
本题其实和452.用最少数量的箭引爆气球 (opens new window)非常像,弓箭的数量就相当于是非交叉区间的数量,只要把弓箭那道题目代码里射爆气球的判断条件加个等号(认为[0,1][1,2]不是相邻区间),然后用总区间数减去弓箭数量 就是要移除的区间数量了。
我们先根据每个小数组的第一个元素进行左边界排序,左排序我们可以直接求重叠的区间,count为记录重叠区间数。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
int count=0;
Arrays.sort(intervals,(a,b)->{
return a[0]-b[0];//按照每个小数组的第一位元素升序
});
//左边界排序可不可以呢?也是可以的,只不过 左边界排序我们就是直接求 重叠的区间,count为记录重叠区间数。
for(int i=0;i<intervals.length-1;i++){
if(intervals[i][1]>intervals[i+1][0]){//有重叠情况
intervals[i+1][1]=Math.min(intervals[i+1][1],intervals[i][1]);
count++;
}
}
return count;
}
}763.划分字母区间
思路不难,但是难以想到,所以一般做过一遍才能有的思路
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。如图

步骤:
1.我们首先要找出s中每个字母最后出现的位置(下标),每个字母的最远位置记录在edge数组中
如上面图中得到的edge:[8,5,7,14,15,11....]
2.分割字符串s,我们遍历字符串s,
下面这里很巧妙,因为我们字符串s中遍历的时候字符混合在一起,相邻间就可能是不同的字符,那么我们要找到这些字符中哪一个字符出现的位置最远,就需要不断更新idx
idx=Math.max(idx,edge[s.charAt(i)-'a']);//代码实现
class Solution {
public List<Integer> partitionLabels(String s) {
//同一字母最多出现在一个片段中。划分成尽可能多的片段
// 返回一个表示每个字符串片段的长度的列表。
List<Integer> list=new LinkedList<>();
//记录每个字母出现的最远位置
int[] edge=new int[26];
for(int i=0;i<s.length();i++){
edge[s.charAt(i)-'a']=i;//会不断更新edge对应字母的值,
}
int idx=0;
int last=-1;
//在上面已经得到字母出现的最远位置了,下面可以开始分割字符串s
for(int i=0;i<s.length();i++){
idx=Math.max(idx,edge[s.charAt(i)-'a']);//
if(i==idx){
list.add(idx-last);
last=i;//更新最新的位置
}
}
return list;
}
}56. 合并区间
这次是二刷了,比之前清楚了许多,思路也好理解
首先对数组按照第一个元素进行升序排列,定义一个区间[start,rightmostBound],初始化:
int start=intervals[0][0];
int rightmostBound=intervals[0][1];
然后开始遍历数组intervals,判断当前遍历的数组与区间有没有重复的范围,有重复则要合并区间,没有重复范围就需要将其添加到结果列表res中,同时更新区间范围
代码实现
class Solution {
public int[][] merge(int[][] intervals) {
// 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
List<int[]> res=new LinkedList<>();
Arrays.sort(intervals,(a,b)->{
return a[0]-b[0];//升序排序
});
int start=intervals[0][0];
int rightmostBound=intervals[0][1];
for(int i=1;i<intervals.length;i++){
if(intervals[i][0]>rightmostBound){
//说明没有重叠
res.add(new int[]{start,rightmostBound});
//更新start和最大右边界
start=intervals[i][0];
rightmostBound=intervals[i][1];
}
else{//intervals[i][0]<=rightmostBound
//说明当前遍历到的intervals[i]和[start,rightmostBound]有重叠的部分
//更新最大右边界
rightmostBound=Math.max(rightmostBound,intervals[i][1]);
}
}
res.add(new int[]{start,rightmostBound});
return res.toArray(new int[res.size()][]);
}
}





![mysql:[Some non-transactional changed tables couldn‘t be rolled back]不支持事务](https://img-blog.csdnimg.cn/45ec3044796e427aa05b6f169fc3c9e4.png)