【C++代码】用栈实现队列，用队列实现栈--代码随想录

队列是先进先出，栈是先进后出。卡哥给了关于C++方向关于栈和队列的4个问题：
- C++中stack 是容器么？
- 使用的stack是属于哪个版本的STL？
- 使用的STL中stack是如何实现的？
- stack 提供迭代器来遍历stack空间么？
首先大家要知道栈和队列是STL（C++标准库）里面的两个数据结构。C++标准库是有多个版本的，要知道我们使用的STL是哪个版本，才能知道对应的栈和队列的实现原理。接下来介绍的栈和队列也是SGI STL里面的数据结构，知道了使用版本，才知道对应的底层实现。来说一说栈，栈先进后出，如图所示：
- 栈提供push 和 pop 等等接口，所有元素必须符合先进后出规则，所以栈不提供走访功能，也不提供迭代器(iterator)。不像是set 或者map 提供迭代器iterator来遍历所有元素。
栈是以底层容器完成其所有的工作，对外提供统一的接口，底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。所以STL中栈往往不被归类为容器，而被归类为container adapter（容器适配器）。从下图中可以看出，栈的内部结构，栈的底层实现可以是vector，deque，list 都是可以的，主要就是数组和链表的底层实现。
- 我们常用的SGI STL，如果没有指定底层实现的话，默认是以deque为缺省情况下栈的底层结构。deque是一个双向队列，只要封住一段，只开通另一端就可以实现栈的逻辑了。SGI STL中队列底层实现缺省情况下一样使用deque实现的。栈的特性，对应的队列的情况是一样的。可以指定vector为栈的底层实现，初始化语句如下：
- ```
std::stack<int, std::vector<int> > third;  // 使用vector为底层容器的栈
```
队列中先进先出的数据结构，同样不允许有遍历行为，不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。也可以指定list 为起底层实现，初始化queue的语句如下：
- ```
std::queue<int, std::list<int>> third; // 定义以list为底层容器的队列
```
- 所以STL 队列也不被归类为容器，而被归类为container adapter（容器适配器）。

题目：用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty），实现 MyQueue 类：
- void push(int x) 将元素 x 推到队列的末尾
- int pop() 从队列的开头移除并返回元素
- int peek() 返回队列开头的元素
- boolean empty() 如果队列为空，返回 true ；否则，返回 false
只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

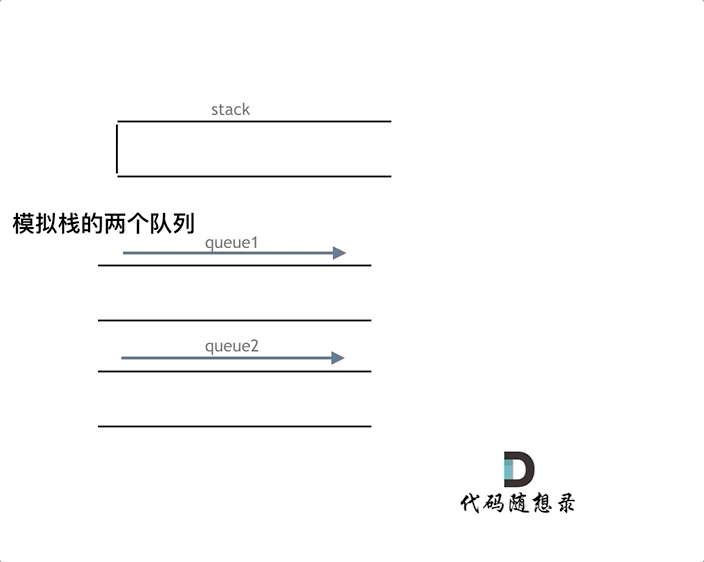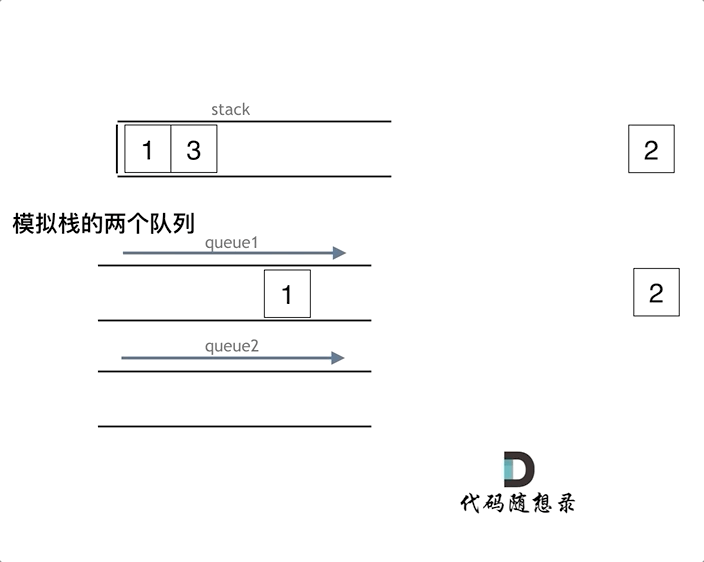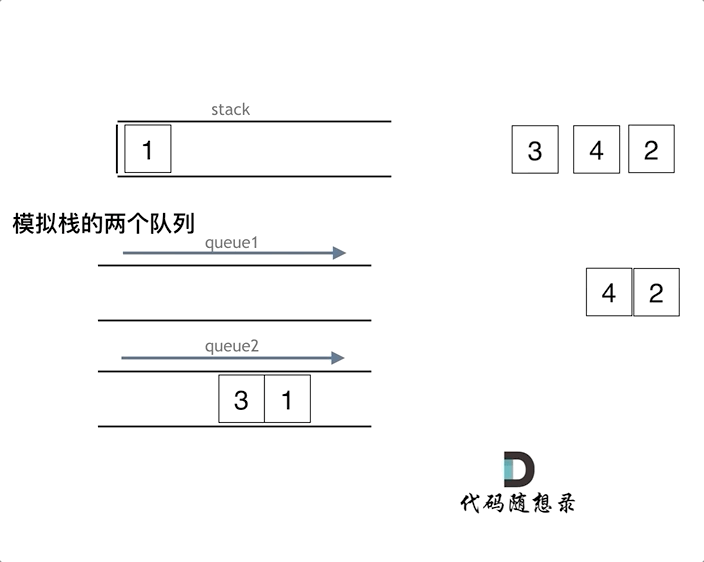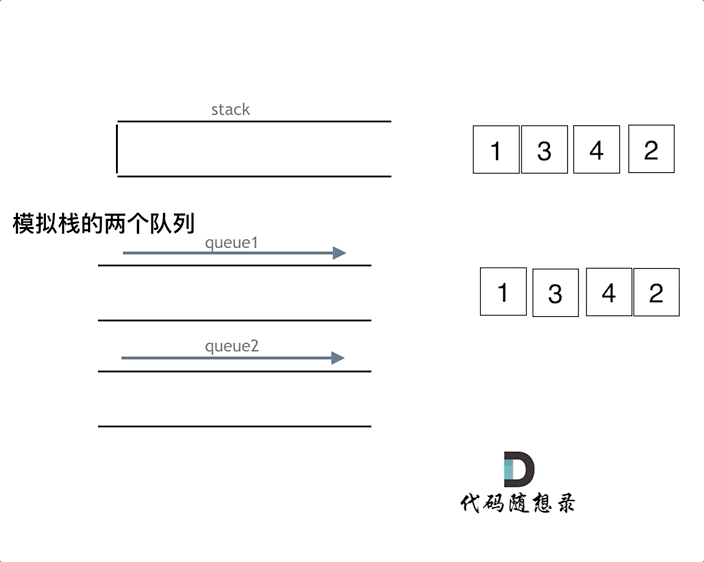
题解

将一个栈当作输入栈，用于压入 push 传入的数据；另一个栈当作输出栈，用于 pop 和 peek 操作。每次 pop 或 peek 时，若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈，这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。

class MyQueue {
private:
    stack<int> inStack,outStack;
    void in2out(){
        while(!inStack.empty()){
            outStack.push(inStack.top());
            inStack.pop();
        }
    }
public:
    MyQueue() {
    }
    void push(int x) {
        inStack.push(x);
    }
    int pop() {
        if(outStack.empty()){
            in2out();
        }
        int res = outStack.top();
        outStack.pop();
        return res;
    }
    int peek() {
        if(outStack.empty()){
            in2out();
        }
        return outStack.top();
    } 
    bool empty() {
        return inStack.empty() && outStack.empty();
    }
};
/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue* obj = new MyQueue();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->peek();
 * bool param_4 = obj->empty();
 */

题目：用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。实现 MyStack 类：
- void push(int x) 将元素 x 压入栈顶。
- int pop() 移除并返回栈顶元素。
- int top() 返回栈顶元素。
- boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。
只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。所使用的语言也许不支持队列。你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

题解

题目涉及到栈和队列两种数据结构。栈是一种后进先出的数据结构，元素从顶端入栈，然后从顶端出栈。队列是一种先进先出的数据结构，元素从后端入队，然后从前端出队。
为了满足栈的特性，即最后入栈的元素最先出栈，在使用队列实现栈时，应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作，其中 queue1 用于存储栈内的元素，queue2 作为入栈操作的辅助队列。
入栈操作时，首先将元素入队到 queue2 ，然后将 queue1 的全部元素依次出队并入队到 queue2 ，此时 queue2 的前端的元素即为新入栈的元素，再将 queue1 和 queue2 互换，则 queue1 的元素即为栈内的元素，queue1 的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保 queue1 的前端元素为栈顶元素，因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除 queue1 的前端元素并返回即可，获得栈顶元素操作只需要获得 queue1 的前端元素并返回即可（不移除元素）。由于 queue1 用于存储栈内的元素，判断栈是否为空时，只需要判断 queue1 是否为空即可。

class MyStack {
private:
    queue<int> queue1;
    queue<int> queue2;
public:
    MyStack() {
    }
    void push(int x) {
        queue2.push(x);
        while(!queue1.empty()){
            //C++ 函数 std::queue::front() 返回对队列第一个元素的引用。 对队列执行 pop 操作后，该元素将被删除。
            queue2.push(queue1.front());
            queue1.pop();
        }
        swap(queue1,queue2);
    }
    int pop() {
        int pop_val = queue1.front();
        queue1.pop();
        return pop_val;
    }
    int top() {
        return queue1.front();
    }
    
    bool empty() {
        return queue1.empty();
    }
};
/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack* obj = new MyStack();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->top();
 * bool param_4 = obj->empty();
 */

时间复杂度：入栈操作 O(n)，其余操作都是 O(1)，其中 n 是栈内的元素个数。入栈操作需要将 queue1 中的 n 个元素出队，并入队 n+1 个元素到 queue2，共有 2n+1 次操作，每次出队和入队操作的时间复杂度都是 O(1)，因此入栈操作的时间复杂度是 O(n)。出栈操作对应将 queue1 的前端元素出队，时间复杂度是 O(1)。获得栈顶元素操作对应获得 queue1 的前端元素，时间复杂度是 O(1)。判断栈是否为空操作只需要判断 queue1 是否为空，时间复杂度是 O(1)。
空间复杂度：O(n)，其中 n 是栈内的元素个数。需要使用两个队列存储栈内的元素。
其实这道题目就是用一个队列就够了。一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外）重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。

class MyStack {
private:
    // queue<int> queue1;
    // queue<int> queue2;
    queue<int> one_queue;
public:
    MyStack() {
    }
    // void push(int x) {
    //     queue2.push(x);
    //     wile(!queue1.empty()){
    //         //C++ 函数 std::queue::front() 返回对队列第一个元素的引用。 对队列执行 pop 操作后，该元素将被删除。
    //         queue2.push(queue1.front());
    //         queue1.pop();
    //     }
    //     swap(queue1,queue2);
    // }
    void push(int x){
        int queue_size = one_queue.size();
        one_queue.push(x);
        for(int i=0;i<queue_size;i++){
            one_queue.push(one_queue.front());
            one_queue.pop();
        }
    }
    // int pop() {
    //     int pop_val = queue1.front();
    //     queue1.pop();
    //     return pop_val;
    // }
    int pop(){
        int top_val = one_queue.front();
        one_queue.pop();
        return top_val;
    }
    // int top() {
    //     return queue1.front();
    // }
    int top(){
        return one_queue.front();
    }
    // bool empty() {
    //     return queue1.empty();
    // }
    bool empty(){
        return one_queue.empty();
    }
};

Queue 队列是一种设计用于在 FIFO（先进先出）上下文中操作的数据结构。 队列中的元素从 rear 端插入并从 front 端移除。Queue 队列类是容器适配器。容器是保存相同类型数据的对象。队列可以从不同的序列容器创建。容器适配器不支持迭代器，因此我们不能将它们用于数据操作。但是它们分别支持 push() 和 pop() 成员函数用于数据插入和删除。
下面是来自 <queue> 头文件的 std::queue 的定义
- ```
template <class T, class Container = deque<T> > class queue;
```
- T − 包含的元素的类型。T 可以替换为任何其他数据类型，包括用户定义的类型。Container − 基础容器对象的类型。
<queue> 中的函数

方法	说明
queue::queue	构造一个具有零个元素的空队列对象。
queue::~queue	通过释放容器内存来销毁队列。
queue::back	返回对队列最后一个元素的引用。
queue::front	返回对队列第一个元素的引用。
queue::emplace	在队列末尾构造并插入新元素。
queue::empty	测试队列是否为空。
queue::pop	删除队列的前面元素。
queue::push	在队列末尾插入新元素。
queue::operator=	通过替换旧内容将新内容分配给队列。
queue::size	返回队列中存在的元素总数。
queue::swap	将队列的内容与另一个队列的内容交换。

堆栈是一种设计用于在 LIFO（后进先出）上下文中运行的数据结构。在堆栈中，元素被插入以及仅从一端移除。Stack 类是容器适配器。容器是保存相同类型数据的对象。可以从不同的序列容器创建堆栈。如果未提供容器，则使用默认的 deque 容器。容器适配器不支持迭代器，因此我们不能将它们用于数据操作。但是它们分别支持 push() 和 pop() 成员函数用于数据插入和删除。下面是来自 <stack> 头文件的 std::stack 定义
- ```
template <class T, class Container = deque<T> > class stack;
```

<stack> 中的成员函数

方法	说明
stack::emplace	在栈顶构造并插入新元素。
stack::empty	测试堆栈是否为空。
stack::operator=	通过替换旧内容将新内容分配给堆栈。
stack::pop	从堆栈中移除顶部元素。
stack::push	在栈顶插入新元素。
stack::size	返回堆栈中存在的元素总数。
stack::swap	将堆栈的内容与另一个堆栈的内容交换。
stack::top	返回对栈顶元素的引用。