神经网络--感知机

news2025/1/24 11:44:39

感知机

单层感知机原理

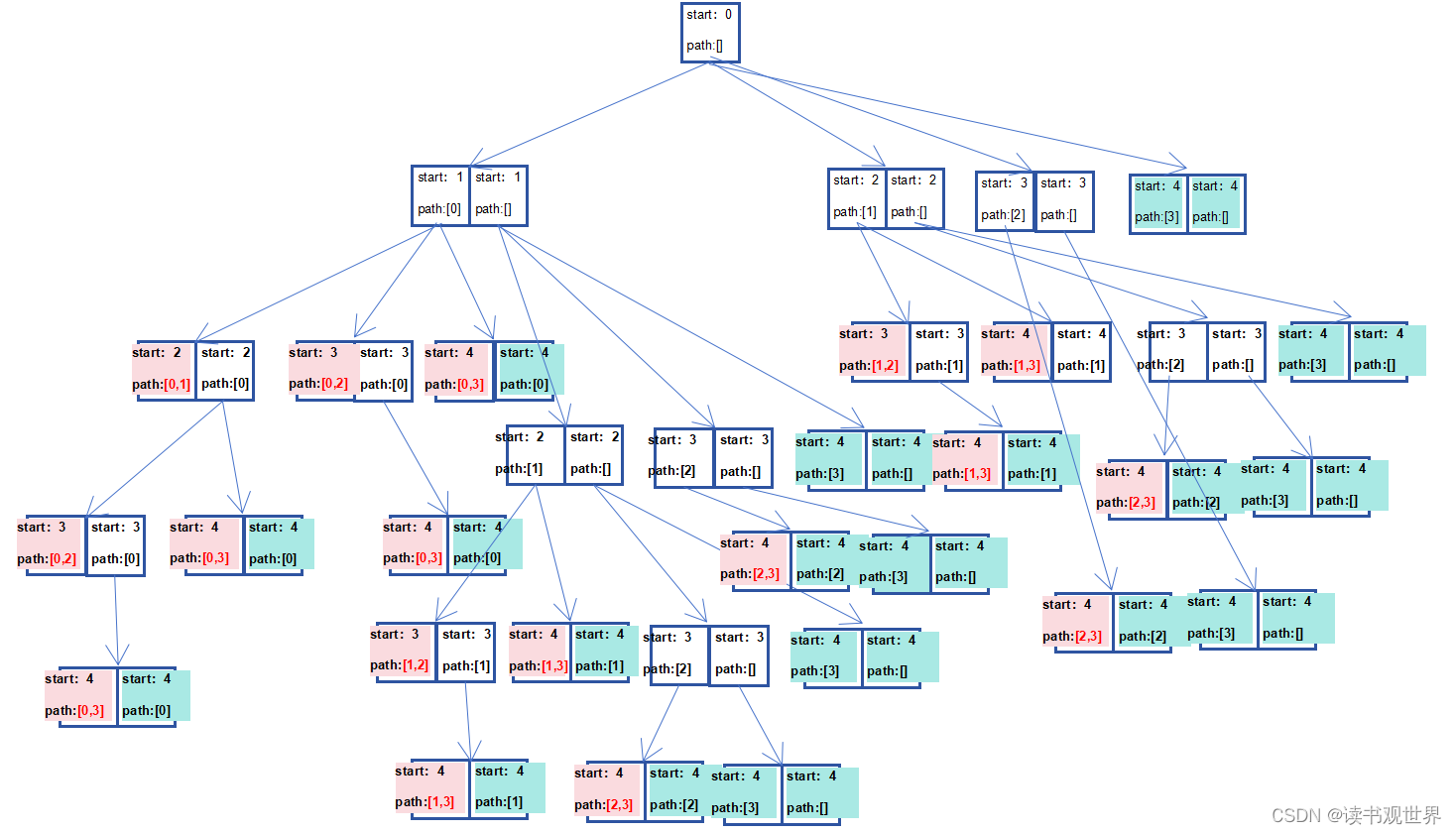
单层感知机:解决二分类问题，激活函数一般使用sign函数,基于误分类点到超平面的距离总和来构造损失函数,由损失函数推导出模型中损失函数对参数 $w$ 和 $b$ 的梯度，利用梯度下降法从而进行参数更新。让+1代表A类，0代表B类。

以下是原理示意图：

在这里插入图片描述

神经元会计算传送过来的信号的总和，当这个总和超过了阈值 $θ$ 时，才会输出1。这也称为“神经元被激活”。
$二进制步进函数\\ y = \begin{cases} 1, w^Tx+b>\theta\\ 0, w^Tx+b<\theta \end{cases}$

损失函数：基于误分类点到超平面的距离总和
$点(x,y)到直线(Ax+By+C=w^Tx+b=0)距离:d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\frac{|w^Tx+b|}{||w||}$

$\sum_{i=1}^{m}{-{y_i(w^Tx_i+b)}}$

$\frac{\partial Loss}{\partial w} = -\sum^{m}_{i=1}y_ix_i\\ \frac{\partial Loss}{\partial b} = -\sum^{m}_{i=1}y_i$

感知机训练算法

$1：感知机训练算法**\\ 初始化参数 w= 0, b= 0\\ repeat:\{ 从训练集随机采样一个样本(x_i, y_i) \\ 计算感知机的输出 t = f(w^T x_i + b),f(x)=1,x>0; f(x)=0, x \leq 0\\ 如果t ≠ y_i：\\ 更新权值:w ← w + \eta (y_i-t)x_i \\ 更新偏移量:b ← b + \eta (y_i-t)\\ \}until 训练次数达到要求输出:分类网络参数w和b,其中\eta 为学习率。$

单层感知机返回的 $w^T+b=0$ 构成一条直线，这也是单层感知机的局限，可以实现与门、与非门(与门取反）、或门三种逻辑电路，无法实现异或门（XOR，（与非门和或门）的与）逻辑电路.

在这里插入图片描述

反向传播算法

在这里插入图片描述

正确理解误差反向传播法，有两种方法：

一种是基于数学式—微分链；

另一种是基于计算图（computational graph）,直观地理解误差反向传播法。

计算图

在这里插入图片描述

在计算图上，从左向右进行计算是正方向上的传播，简称为正向传播（forward propagation）。正向传播是从计算图出发点到结束点的传播。当然从图上看，从右向左的传播,称为反向传播（backward propagation）。反向传播在导数计算中发挥重要作用。
在这里插入图片描述

假设我们想知道苹果价格的上涨会在多大程度上影响最终的支付金额，即求“支付金额关于苹果的价格的导数”。这个导数的值表示当苹果的价格稍微上涨时，支付金额会增加多少。反向传播使用与正方向相反的箭头（粗线）表示。反向传播传递“局部导数”，将导数的值写在箭头的下方。在这个例子中，反向传播从右向左传递导数的值（1→1.1→2.2）。从这个结果中可知，“支付金额关于苹果的价格的导数”的值是2.2。这意味着，如果苹果的价格上涨1元，最终的支付金额会增加2.2元（严格地讲，如果苹果的价格增加某个微小值，则最终的支付金额将增加那个微小值的2.2倍）

链式法则

在这里插入图片描述

加法节点

在这里插入图片描述

乘法节点

在这里插入图片描述

激活节点

1.relu

在这里插入图片描述

2.sigmoid函数

计算图的反向传播:

步骤1:
“/”节点表示 $y=\frac{1}{x}$ ，它的导数可以解析性地表示为: $\frac{\partial y}{\partial x} = -\frac{1}{x^2} = -y^2$ 。反向传播时，会将上游的值乘以−y2（正向传播的输出的平方乘以−1后的值）后，再传给下游。计算图如下所示。
步骤2:
“+”节点将上游的值原封不动地传给下游。计算图如下所示.

在这里插入图片描述

步骤3:
“exp”节点表示: $y = e x p (x)$ ，它的导数: $\frac{\partial y}{\partial x} = exp(x)$ 。
计算图中，上游的值乘以正向传播时的输出（例中是exp(−x)）后，再传给下游。
步骤4: “×”节点将正向传播时的值翻转后做乘法运算。因此，这里要乘以−1。