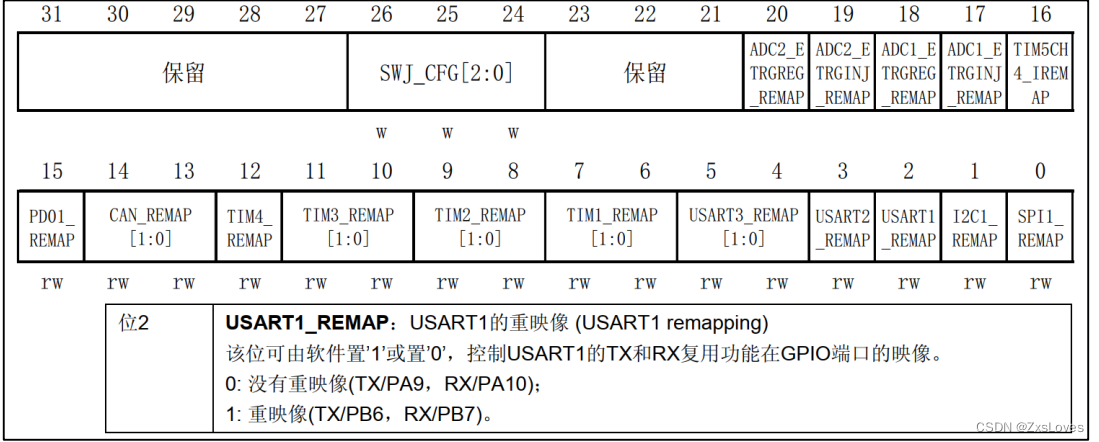
题目
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
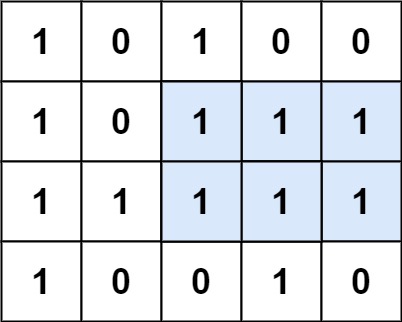
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出:6 解释:最大矩形如上图所示。
示例 2:
输入:matrix = [] 输出:0
示例 3:
输入:matrix = [["0"]] 输出:0
示例 4:
输入:matrix = [["1"]] 输出:1
示例 5:
输入:matrix = [["0","0"]] 输出:0
提示:
rows == matrix.lengthcols == matrix[0].length1 <= row, cols <= 200matrix[i][j]为'0'或'1'
解答
源代码
class Solution {
public int maximalRectangle(char[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int[] heights = new int[n];
int maxArea = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
heights[j] += 1;
} else {
heights[j] = 0;
}
}
maxArea = Math.max(maxArea, largestRectangleArea(heights));
}
return maxArea;
}
public int largestRectangleArea(int[] heights) {
int[] left = new int[heights.length];
int[] right = new int[heights.length];
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < heights.length; i++) {
while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
stack.pop();
}
left[i] = stack.isEmpty() ? -1 : stack.peek();
stack.push(i);
}
stack.clear();
for (int i = heights.length - 1; i >= 0; i--) {
while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
stack.pop();
}
right[i] = stack.isEmpty() ? heights.length : stack.peek();
stack.push(i);
}
int maxArea = 0;
for (int i = 0; i < heights.length; i++) {
maxArea = Math.max(maxArea, (right[i] - left[i] - 1) * heights[i]);
}
return maxArea;
}
}总结
这题是建立在「84.柱形图中最大的矩形」上进行解答的,最第一行到最后一行,把当前行到最上面看作一个柱形图,计算出每列的高度,利用 「84.柱形图中最大的矩形」的函数进行计算,最终比较得到最大值。


![[管理与领导-65]:IT基层管理者 - 辅助技能 - 4- 乌卡时代(VUCA )](https://img-blog.csdnimg.cn/bd74b0eaebd74ba7b678af58b858d5f1.png)