bezier曲线在编程中的难点在于求取曲线的系数,如果系数确定了那么就可以用微小的直线段画出曲线。bezier曲线的系数也就是bernstein系数,此系数的性质可以自行百度,我们在这里是利用bernstein系数的递推性质求取:
简单举例
两个点p0,p1 为一阶曲线,系数为 (1-u)p0+u*p1; 将系数存在数组中b[0] =1-u,b[1]=u。
三个点 p0 p1 p2 为二阶曲线,系数(1-u)(1-u)p0+2u(1-u)p1+u*u*p2 可以看出二阶的系数是一届的系数的关系 ((1-u)+u)(b[0]+b[1])。
注意:通过这个公式有没有发现,当u==0的时候这个点就是p0,当u==1的时候这个点就是p2,其他时候点被p1所吸引,也就是p1点的存在会导致(u!=0&&u!=1)的时候生成的点靠近p1。
四个点 三阶曲线为:
((1-u)+u)((1-u)+u)(b[0]+b[1])
是不是有种似曾相识的感觉,对了,这就是高中牛顿二项式展开的过程:

二阶贝塞尔曲线实现代码:
QPointF p0(0,0);
QPointF p1(1000,0);
QPointF p2(1000,1000);
QPainterPath path;
path.moveTo(p0);
QPointF pTemp;
for(double t=0; t<1; t+=0.01) //2次Bezier曲线
{
pTemp =pow((1-t),2)*p0+2*t*(1-t)*p1+pow(t,2)*p2;
path.lineTo(pTemp);
}没有使用贝塞尔曲线(三个点直接相连)画出来三角形是这样:

使用贝塞尔曲线之后,(1000,0)这个位置的角会圆化:
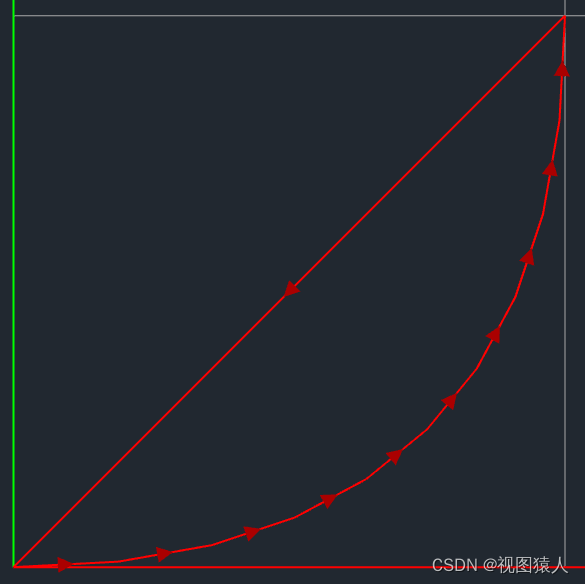
上图中你会发现曲线不太圆滑,这个你可以调参数precision,主要的问题是它用了贝塞尔曲线之后都不像一个三角形了,我们只想对三角形的角进行圆化。我们可以选择构成三角形角的两边上接近交点位置的两个点,用这个两个点和这两边的交点(三角形的角)生成贝塞尔曲线,效果如下:
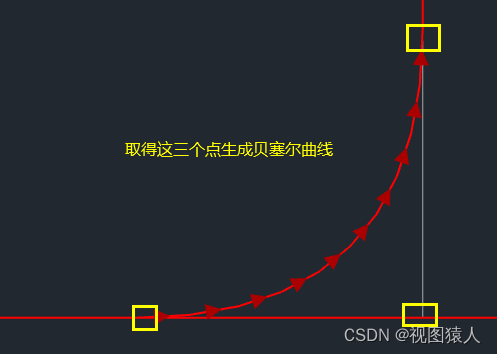
我们发现他就是有很多短小的曲线构成的,所以这就是多边形的角圆化的原理。
上面是实现的二阶贝塞尔曲线,但是有时候我们可能会使用其他阶数曲线,所以我们需要改一下代码使得代码更大众化:
/**
* @brief createNBezierCurve 生成N阶贝塞尔曲线点
* @param src 源贝塞尔控制点,里面有两个点就是一阶,有三个点就是二阶,依次类推
* @param dest 目的贝塞尔曲线点
* @param precision 生成精度,控制着细小直线的长度,细小直线长度越小模拟出现的圆角越圆滑(此值越小细小直线长度越小)
*/
static void createNBezierCurve(const QList<QPointF> &src, QList<QPointF> &dest, qreal precision=0.5)
{
if (src.size() <= 0) return;
//清空
QList<QPointF>().swap(dest);
//外侧循环控制(1-u)p0+u*p1中u的值,用来生成多个点
for (qreal t = 0; t < 1.0000; t += precision) {
int size = src.size();
QVector<qreal> coefficient(size, 0);
coefficient[0] = 1.000;
qreal u1 = 1.0 - t;
//里面循环用来生成每一次u改变之后的参数值,参数就是二项展开式,然后把参数和各顶点乘起来就得到贝塞尔曲线的一个顶点
for (int j = 1; j <= size - 1; j++) {
qreal saved = 0.0;
for (int k = 0; k < j; k++){
qreal temp = coefficient[k];
coefficient[k] = saved + u1 * temp;
saved = t * temp;
}
coefficient[j] = saved;
}
//最后的贝塞尔顶点
QPointF resultPoint;
for (int i = 0; i < size; i++) {
QPointF point = src.at(i);
resultPoint = resultPoint + point * coefficient[i];
}
dest.append(resultPoint);
}
}然后我来讲讲代码如何实现把三角形的角圆化的:
/*
src就是保存多边形所有顶点的集合,要有序(有序的意思就是按照点的顺序可以形成一个多边形)
dest就是一个空的集合,最后生成的所有点都放在里面,然后按照这些点依次连接最后就是一个角圆化之后的多边形
*/
void GeometryViewer::centralHandler(vector<CVector2d>&src, vector<CVector2d>&dest)
{
vector<CVector2d>tmp;
for (int i = 0; i < src.size(); ++i)
{ //对于每一个多边形顶点(角),我们需要找到构成这个顶点的两条直线上接近顶点的两个点,用这三个点生成贝塞尔曲线
CVector2d pt1 = getLineStart(src[i],src[(src.size() + i - 1) % src.size()]);
tmp.push_back(pt1);
tmp.push_back(src[i]);
CVector2d pt3 = getLineStart(src[i], src[(i + 1) % src.size()]);
tmp.push_back(pt3);
createNBezierCurve(tmp, dest);
tmp.clear();
}
}CVector2d类的功能大致如下:
class CVector2d
{
public:
double X,Y;
CVector2d(double x,double y):X(x),Y(y)
{
X=x;
Y=y;
printf("%lf 00**** %lf\n",x,y);
}
CVector2d operator+(CVector2d y)const
{
return CVector2d(X+y.X,Y+y.Y);
}
};getLineStart它将返回一个点, 该点是pt1顶点朝着pt2顶点离开m_uiRadius像素。变量fRat保持半径与第i个线段长度之间的比率。还有一项检查可以防止fRat的值超过0.5。如果fRat的值超过0.5, 则两个连续的圆角将重叠, 这将导致较差的视觉效果。
当从点P1到点P2直线行驶并完成距离的30%时, 我们可以使用公式0.7•P1 + 0.3•P2确定位置。通常, 如果我们获得完整距离的一小部分, 并且α= 1表示完整距离, 则当前位置为(1-α)•P1 +α•P2。
这就是GetLineStart方法确定在第(i + 1)方向上距离第i个顶点m_uiRadius像素的点的位置的方式。
CVector2d GeometryViewer::getLineStart(CVector2d pt1,CVector2d pt2,double radius=0.0)
{
CVector2d pt;
double fRat;
if(radius==0)
fRat = 0.02;
else fRat = radius / getDistance(pt1, pt2);
if (fRat > 0.5f)
fRat = 0.5f;
pt.X = (1.0f - fRat)*pt1.X + fRat*pt2.X;
pt.Y = (1.0f - fRat)*pt1.Y + fRat*pt2.Y;
return pt;
}//欧几里得距离
double getDistance(CVector2d pt1, CVector2d pt2)
{
double fD = (pt1.X - pt2.X)*(pt1.X - pt2.X) +
(pt1.Y - pt2.Y) * (pt1.Y - pt2.Y);
return sqrt(fD);
}