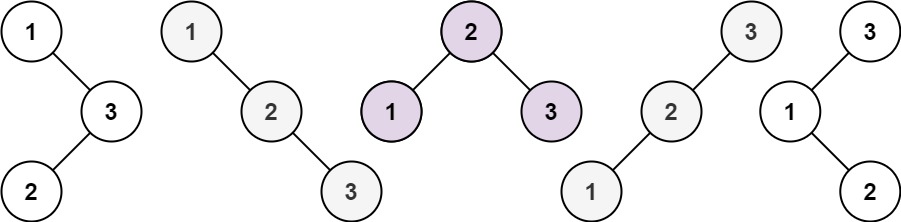
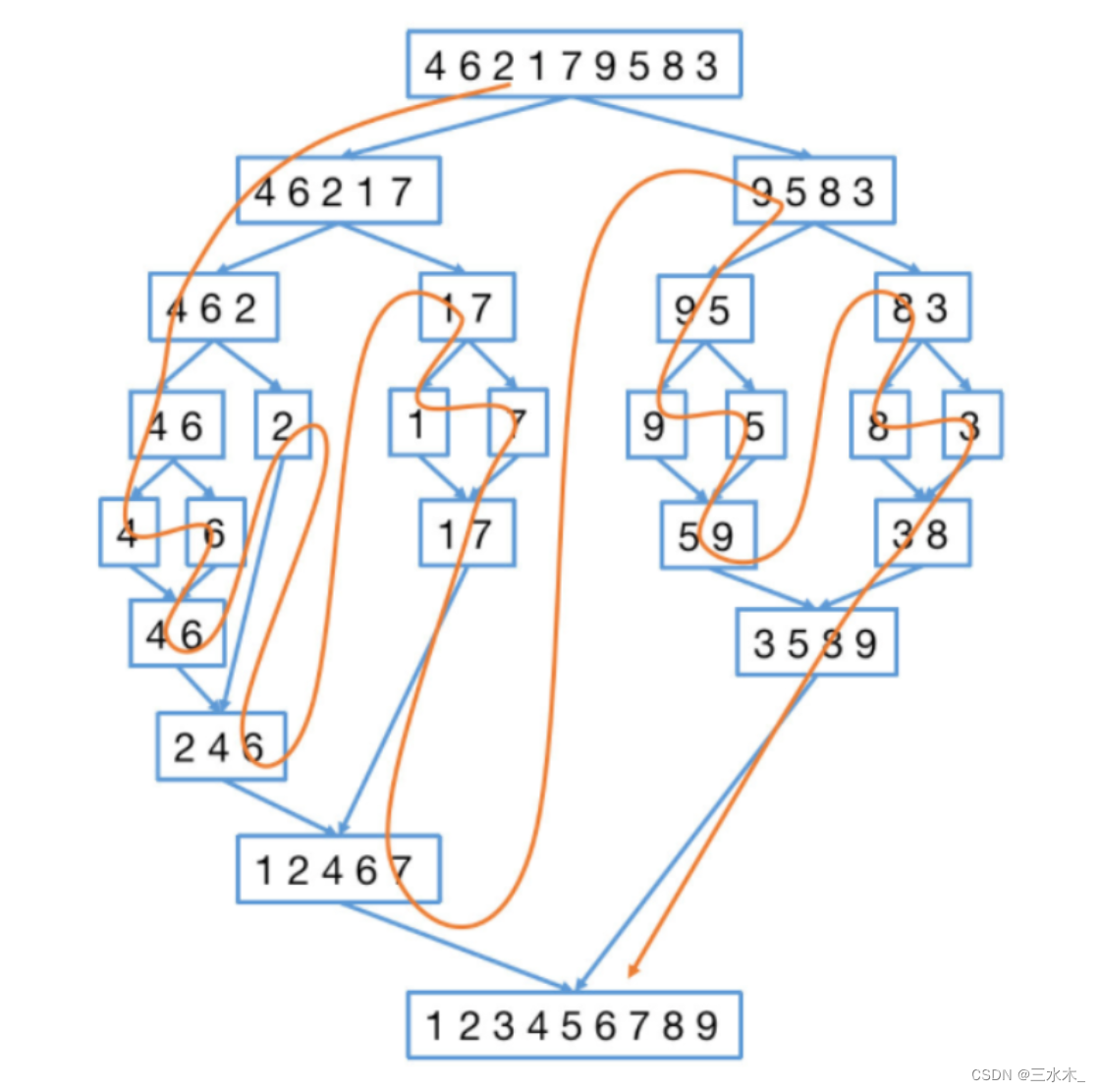
归并排序(Merge Sort)是一种常见的基于比较的排序算法,它的主要思想是分而治之(Divide and Conquer)。它的核心思想是将一个大的问题分解为小的子问题,解决子问题,然后将它们合并(merge)以获得最终的解决方案。
以下是归并排序的详细步骤:
-
分割(Divide):将原始数组划分为两个或更多的子数组。这个过程持续递归,直到每个子数组都只包含一个元素,即认为这些子数组都是有序的。
-
合并(Merge):将两个有序的子数组合并成一个有序的大数组。合并过程是排序的关键步骤。在合并过程中,我们逐个比较两个子数组中的元素,将较小的元素放入新的数组,重复这个过程,直到将两个子数组全部合并为一个有序数组。
-
递归:递归是归并排序的核心。每次分割和合并过程都会递归地调用归并排序,直到整个数组都被排序。
-
结果:最终,当递归结束时,整个数组就会被完全排序。
class Solution {
public int[] sortArray(int[] nums) {
if(nums == null || nums.length == 1){
return nums;
}
sort(nums,0,nums.length - 1);
return nums;
}
public void sort(int[] nums,int start,int end){
if(start == end){
return;
}
sort(nums,start,(start+end)/2);
sort(nums,(start+end)/2+1,end);
merge(nums,start,end);
}
public void merge(int[] nums,int start,int end){
int mid = (start + end)/2;
int[] temp = new int[end - start + 1];
int k = 0;
int i = start;
int j = mid + 1;
while(i <= mid&&j <= end){
if(nums[i]<=nums[j]){
temp[k++] = nums[i++];
}else{
temp[k++] = nums[j++];
}
}
while(i<=mid){
temp[k++] = nums[i++];
}
while(j<=end){
temp[k++] = nums[j++];
}
k=0;
while(start<=end){
nums[start++] = temp[k++];
}
}
}归并排序的时间复杂度是稳定的,它保证在最坏、平均和最好的情况下都是O(n log n)。这使得它在处理大规模数据时非常高效。
归并排序的优点包括:
- 稳定性:相同元素的相对位置在排序前后不会改变,这在某些应用中是非常重要的。
- 适用于大数据集:归并排序的时间复杂度相对较低,因此适用于大规模数据集的排序。
- 可以用于外部排序:归并排序可以轻松地应用于需要外部存储的排序任务。
然而,归并排序的缺点是它需要额外的空间来存储中间结果,因此在内存有限的情况下可能不适用。此外,由于它是基于比较的排序算法,对于小规模数据集来说可能不如一些快速排序算法快速。