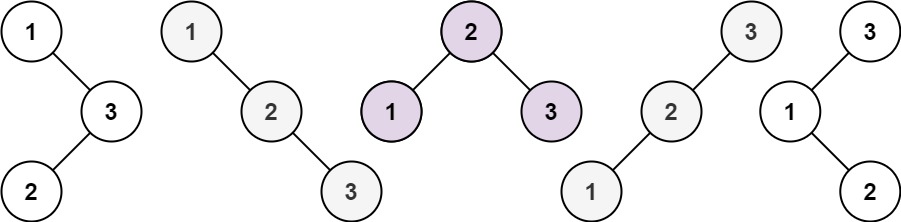
给定一个二叉树，检查它是否是镜像对称的。

——————————————————————————————————————————

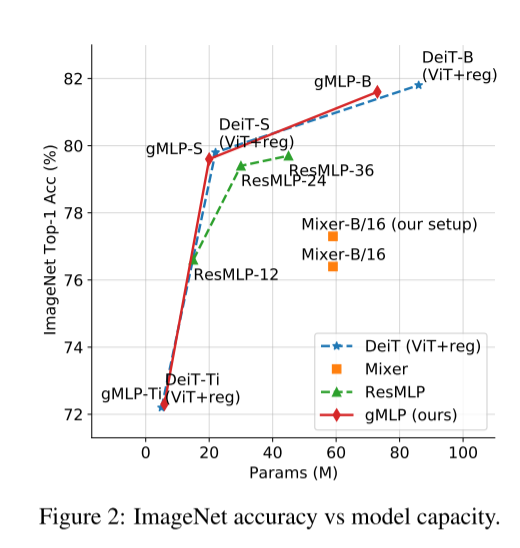
分析：

需要比较的是根节点的左右子树，且是两个子树的里侧和外侧的元素是否相等。

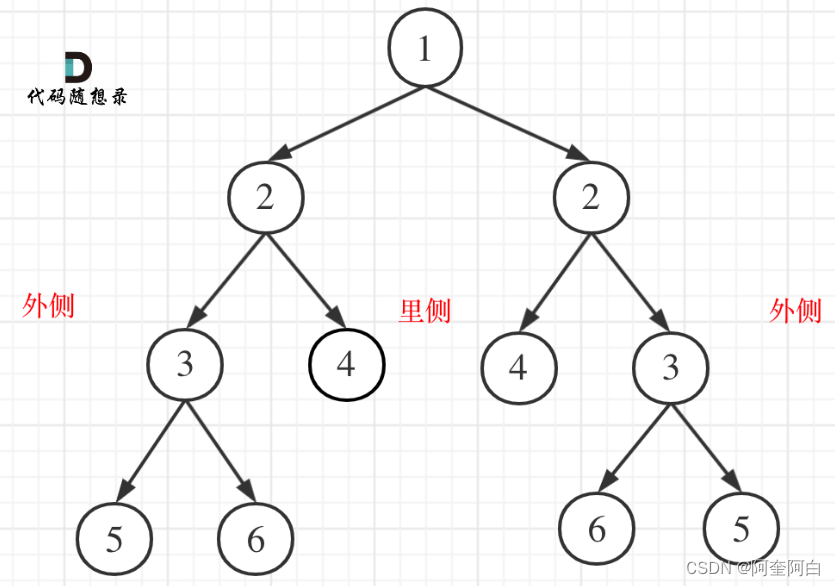
根据后序遍历算法，一颗子树左右中，另一颗右左中遍历，进行比较是否相等。

递归法：

任然是三部曲：首先是递归函数的参数和返回值

确定是否相等，返回BOOL类型即可，传入的参数就是左右节点。

bool campare(TreeNode* left, TreeNode* right)

然后确定终止条件：

        比较两个节点是否相等，要考虑到节点为NULL的情况。

        左右节点有一个为空，返回false，都为空返回True。

        左右节点不为空，若值相等，返回TRUE。

最后确定单层递归的逻辑：

        实际上就是当左右节点不为空且相等后做什么，比较二叉树外侧是否相等，比较内侧是否相等，同时判断内侧和外侧。

简洁写法：逻辑都一样

class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right) {
        if (left == NULL && right != NULL) return false;
        else if (left != NULL && right == NULL) return false;
        else if (left == NULL && right == NULL) return true;
        else if (left->val != right->val) return false;
        else return compare(left->left, right->right) && compare(left->right, right->left);

    }
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return compare(root->left, root->right);
    }
};

迭代法：

使用队列来比较根节点的两个左右子树是否互相翻转。