Communication-Efficient Learning of Deep Networks from Decentralized Data

news2025/2/27 20:50:56

international conference on artificial intelligence and statistics

Summary

当前机器学习模型训练中存在着数据隐私保护问题，所以作者提出了FL概念。通过分布式+隐私保护进行训练模型。对不平衡、non-IID的数据也更合适。
主要提出了FedSGD和FedAvg算法。FedAvg通信代价要小于FedSGD
实验中使用了MNIST数字识别和语言模型，通过改变E和B(client本地训练的轮次、每次训练小批量数据的size)来探究最优的E和B，而且在non-IID和IID两种数据中都进行了相关实验。

Problem and Background

目前我们拥有的一些设备（手机、PC）具有一定的算力，也可以接触到大量的包含个人隐私的数据。而且这些数据相较于传统的分布式学习是unbalanced and non-IID。每个client的数据肯定是不同规模，不同倾向的。
所以我们希望提出一种模型训练的方法，可以在不同的设备上利用本地隐私数据进行模型训练。

Contributions

提出Federal Learning这一概念。可用于人工智能隐私保护和安全多方计算。
FedAvg算法有一定的实用性，用于unbalanced and non-IID dataset，可以用较少的通信轮次获取不错的训练模型。

Method

FedSGD and FedAvg
- C-fraction of clients on each round
- E-本地客户端训练local data的次数
- B-训练时本地数据小批量的大小，就是每次训练用多少数据。当B无穷大就代表每次训练本地的所有数据都要用。
- 当B无穷大，E为1的时候，就是用所有数据每轮训练一次，那就是FedSGD Algorithm。
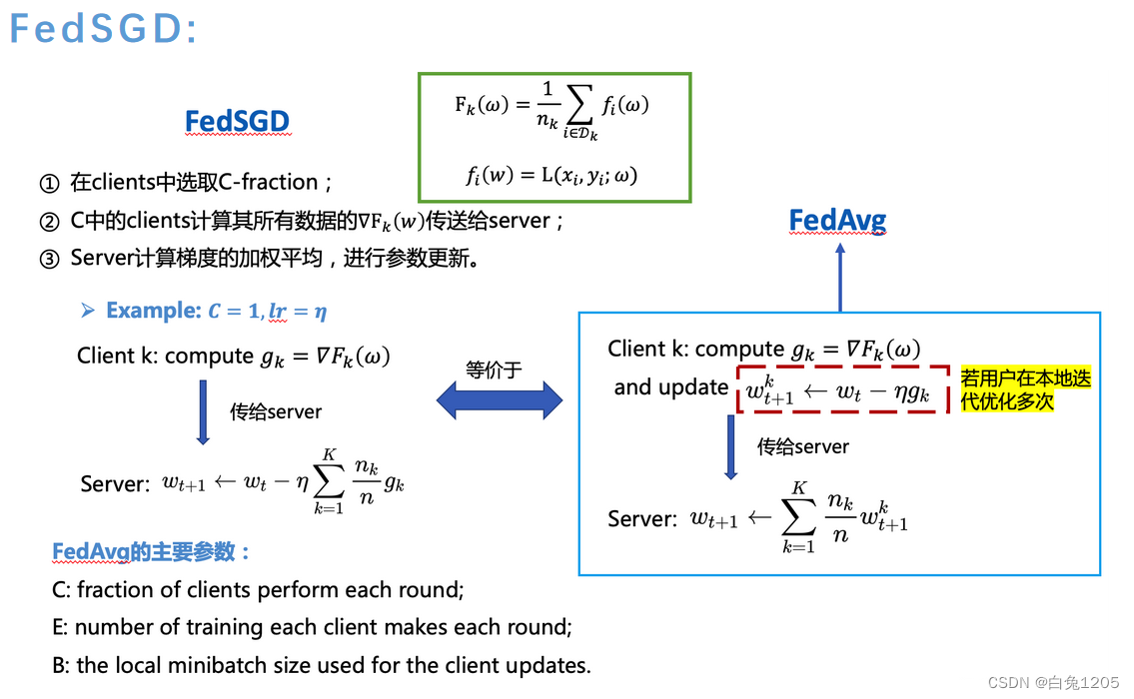- - fedsgd：client发送给server的是g（梯度） - fedavg：client直接用g求出要更新的ω发送给server。
algorithm 1 FedAvg
- 其中服务器平均更新的权重是每个client的数据集占总的数据集的比重。（但是这里有client谎报自己的数据集怎么办，让自己用比较少的dataset占大的比重）

Experimental

MNIST digit recognition
- MNIST 2NN
  - 具有2个隐藏层的多层感知器，每个层使用ReLu激活200个单元(总计199,210个参数)
- CNN
  - CNN有两个5x5卷积层(第一个有32个通道，第二个有64个，每个都有2x2个最大池化)，一个有512个单元和ReLu激活的完全连接层，以及一个最终的Softmax输出层(总参数为1,663,370)。
- 两种数据分发方式：IID and non-IID
  - IID
    Each client随机获得600样例。
  - non-IID
    将用例按数字先分好类，再分成300size的200份。最后每个client只有两个数字的样例。
Language Modeling
- dataset:莎士比亚作品集
- 为作品集中所有说话的角色建立一个client，共1146个。将每个client的数据集八二分，80用于训练，20用于测试。与MNIST数据集不同的是这个每个client的数据是不平衡的，就是训练可用数据多少不同。
- 该模型将一系列字符作为输入，并将每个字符嵌入到学习的 8 维空间中。然后通过 2 个 LSTM 层处理嵌入的字符，每个层有 256 个节点。最后，第二个 LSTM 层的输出被发送到 softmax 输出层，每个字符一个节点。完整模型有 866,578 个参数，我们使用 80 个字符的展开长度进行训练。
Result
- 论文中讲解了相关实验的结果，主要研究了当B和E变化时对实验的影响，当B为10，E为5的时候效果比较好，因为B正无穷，E为1的时候就成立FedSGD。

Related Knowledge

SGD

利用梯度觉得接下来迭代的方向，使代价函数越来越小。
SGD为随机梯度下降法。用数学式可以将 SGD 写成如下的式（6.1）。

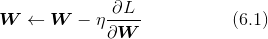
这里把需要更新的权重参数记为W，把损失函数关于W的梯度记为 ∂L/∂W 。η ηη 表示学习率，实际上会取 0.01 或 0.001 这些事先决定好的值。式子中的←表示用右边的值更新左边的值。
————————————————
版权声明：本文为CSDN博主「赵孝正」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_46713695/article/details/123198293

import matplotlib.pyplot as plt
#一元四次函数 f(x) = x^4 - 3x^3+2
xold = 0
xnew = 6

#误差
eps = 0.00002
#步长，学习率
alpha = 0.01
#function
x = []
y = []
plt.title="TrendofSGD"
plt.xlabel('x')
plt.ylabel('y')

def f(x):
    return x ** 4 - 3 * x ** 3 + 2
def f_prime(x):#倒数
    return 4 * x ** 3 - 9 * x ** 2
while abs(f(xold)-f(xnew)) > eps:
    xold = xnew
    xnew = xold - alpha * f_prime(xold)
    x.append(xnew)
    y.append(f(xnew))
    plt.scatter(xnew,f(xnew))
    plt.pause(0.2)
plt.plot(x,y)
plt.show()
print(x)
print("Result:",xnew,f(xnew))

卷积层
- (10 条消息) 如何通俗易懂地解释卷积？ - 知乎 (zhihu.com)
- (27条消息) 卷积层详述_Zeus_dad的博客-CSDN博客_卷积层
池化
- 池化 | 机器之心 (jiqizhixin.com)
完全连接层
- CNN 入门讲解：什么是全连接层（Fully Connected Layer）? - 知乎 (zhihu.com)
ReLu activation
- 原来ReLU这么好用！一文带你深度了解ReLU激活函数！ - 知乎 (zhihu.com)
- 考虑输入输出及数据变化来选择用什么激活函数
softmax output
- [(27条消息) 神经网络中的softmax层为何可以解决分类问题——神经网络之softmax(3)_石头1666的博客-CSDN博客_softmax分类层](