线性DP问题

news2025/4/17 15:15:41

目录

  • 数字三角形
    • DP 动态规划 [自上向下+二维数组]
    • DP 动态规划 [自上向下+一维数组]
    • DP 动态规划 [自下而上+二维数组]
    • DP 动态规划 [自下而上+一维数组]
    • 记忆化搜索 + DFS
  • 最长上升子序列
    • 一维状态数组实现
    • 扩展：最长序列输出
  • 最长上升子序列 II
    • 贪心+二分优化
      • 算法思路
      • 代码实现
      • 扩展： 最长序列输出
  • 最长公共子序列
    • 算法思路
    • 代码实现
  • 最短编辑距离
    • 算法思路
    • 代码实现
  • 编辑距离
    • 代码实现

数字三角形

题目描述：
给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

输入格式：
第一行包含整数 n n n，表示数字三角形的层数。

接下来 n n n 行，每行包含若干整数，其中第 i i i 行表示数字三角形第 i i i 层包含的整数。

输出格式：
输出一个整数，表示最大的路径数字和。

数据范围：
1 ≤ n ≤ 500 , − 10000 ≤ 1≤n≤500,−10000≤ 1≤n≤500,−10000≤三角形中的整数 ≤ 10000 ≤10000 ≤10000

输入样例：

5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5

输出样例：

30

DP 动态规划 [自上向下+二维数组]

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 510;
int a[N][N], f[N][N];

int main()
{
	int n;
	cin >> n;
	memset(a, -0x3f, sizeof a);
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 1; j <= i; ++j)
		{
			cin >> a[i][j];
			f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
		}
	}
	int res = -0x3f;
	for (int i = 1; i <= n; ++i) res = max(res, f[n][i]);
	cout << res << endl;
	return 0;
}

DP 动态规划 [自上向下+一维数组]

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 510;
int a[N][N], f[N];
int main()
{
	int n;
	cin >> n;
	memset(a, -0x3f, sizeof a);
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 1; j <= i; ++j)
			cin >> a[i][j];
	}
	for (int i = 1; i <= n; ++i)
	{
		for (int j = i; j >= 0; --j)
			f[j] = max(f[j - 1], f[j]) + a[i][j];
	}
	int res = -0x3f;
	for (int i = 1; i <= n; ++i) res = max(res, f[i]);
	cout << res << endl;
	return 0;
}

DP 动态规划 [自下而上+二维数组]

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 510;
int a[N][N], f[N][N];

int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= i; ++j)
			cin >> a[i][j];
	for (int i = n; i >= 1; --i)
	{
		for (int j = 1; j <= n; ++j)
			f[i][j] = max(f[i + 1][j + 1], f[i + 1][j]) + a[i][j];
	}
	cout << f[1][1] << endl;
	return 0;
}

DP 动态规划 [自下而上+一维数组]

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 510;
int a[N][N], f[N];

int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= i; ++j)
			cin >> a[i][j];
	for (int i = n; i >= 1; --i)
	{
		for (int j = 1; j <= n; ++j)
			f[j] = max(f[j + 1], f[j]) + a[i][j];
	}
	cout << f[1] << endl;
	return 0;
}

记忆化搜索 + DFS

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 510;
int n, f[N][N], a[N][N];

int dfs(int u, int k)
{
	if (~f[u][k]) return f[u][k];
	if (k > u || u == n + 1) return 0; // 限制范围
	return f[u][k] = max(dfs(u + 1, k + 1), dfs(u + 1, k)) + a[u][k];
}
int main()
{
	cin >> n;
	memset(f, -1, sizeof f);
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= i; ++j) cin >> a[i][j];
	cout << dfs(1, 1) << endl;
	return 0;
}

最长上升子序列

题目描述：
给定一个长度为 N N N 的数列，求数值 严格单调递增的子序列 的长度最长是多少。

输入格式：
第一行包含整数 N N N。

第二行包含 N N N 个整数，表示完整序列。

输出格式：
输出一个整数，表示最大长度。

数据范围：
1 ≤ N ≤ 1000 ， − 1 0 9 ≤ 1≤N≤1000，−10^9≤ 1≤N≤1000，−109≤数列中的数 ≤ 1 0 9 ≤10^9 ≤109

输入样例：

7
3 1 2 1 8 5 6

输出样例：

4

一维状态数组实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1010;
int f[N], a[N];

int main()
{
	int n, res = 1;
	cin >> n;
	for (int i = 1; i <= n; ++i)
	{
		cin >> a[i];
		f[i] = 1;
		for (int j = 1; j <= i; ++j)
			if (a[i] > a[j]) f[i] = max(f[i], f[j] + 1);
	}
	cout << f[n] << endl;
	return 0;
}

扩展：最长序列输出

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1010;

int n, a[N];
int f[N];
int res, pos; // LIS最大长度  pos:最大长度是哪个下标数字提供
int pre[N];  //记录转移的前序关系

//循环+vector方式打印路径
void print(int k) {
    vector<int> path; //因为查找的关系是逆序的，需要用一个向量数组把这个逆序反过来，才能输出
    while (k) {
        path.push_back(a[k]);
        k = pre[k];
    }
    //倒序输出LIS序列
    for (int i = path.size() - 1; i >= 0; i--) printf("%d ", path[i]);
}

//递归方式打印路径
//这个递归输出逆序路径，真是太妙了，把递推与逆序的通用性展示的淋漓尽致，把别人正常用7行才能完成的代码，它只需要2行，真是太精炼了，又好写又好记。
void out(int k) {
    if (pre[k]) out(pre[k]); //因为最前面的第1号，它的前序
    printf("%d ", a[k]);
}

int main() {
    scanf("%d", &n);

    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i++) {
        f[i] = 1;
        for (int j = 1; j < i; j++)
            if (a[i] > a[j] && f[i] <= f[j]) {
                f[i] = f[j] + 1;
                pre[i] = j; // f[i]的前序是f[j]
            }

        // 更新最大值
        if (f[i] > res) {
            res = f[i]; //记录LIS最大值
            pos = i;    //记录LIS最大值时相应的数组下标i
        }
    }

    //输出LIS最大长度
    printf("%d\n", res);

    //输出前序数组查看情况
    for (int i = 1; i <= n; i++) cout << pre[i] << " ";
    puts("");

    //循环+vector方式输出LIS路径
    //从最大LIS值的下标开始，配合pre数组，不断向前以蛇形方式逆序查找前序
    print(pos);

    puts("");

    //递归方式输出LIS路径
    out(pos);

    return 0;
}

最长上升子序列 II

题目描述：
给定一个长度为 N N N 的数列，求数值 严格单调递增的子序列 的长度最长是多少。

输入格式：
第一行包含整数 N N N。

第二行包含 N N N 个整数，表示完整序列。

输出格式：
输出一个整数，表示最大长度。

数据范围：
1 ≤ N ≤ 100000 1≤N≤100000 1≤N≤100000， − 1 0 9 ≤ −10^9≤ −109≤数列中的数 ≤ 1 0 9 ≤10^9 ≤109

输入样例：

7
3 1 2 1 8 5 6

输出样例：

4

贪心+二分优化

算法思路

核心思想:
对于同样长度的子串，希望它的末端越小越好，这样后面有更多机会拓展它，才有可能使得数列更长。

算法步骤：

扫描每个原序列中的数字：
如果 q q q 中的最后一个数字 q [ i d x ] q[idx] q[idx] 小于当前数字 a [ i ] a[i] a[i]，那么就在 q q q 的最后面增加 a [ i ] a[i] a[i]。
如果 a [ i ] a[i] a[i] 小于 q [ i d x ] q[idx] q[idx]，在 q q q 中查找并替换第一个大于等于它元素。

模拟过程：

a3121856

开始时 q [ ] q[] q[] 为空，数字3进入序列。

arr3121856
q3

1 比 3 小，3出序列 ，1入序列。

a3121856
q1

比 1 大，2入序列。

a3121856
q1
a3121856
q12

比 2 小，在 q q q 中找到第一个大于等于1的位置，并替换掉原来的数字。

a3121856
q12

8 比 2 大，入序列。

a3121856
q128

5 比 8 小，在 q q q 中找到第一个大于等于5的数字，并替换掉原来的数字。

a3121856
q125

6 比 5 大，入序列。

a3121856
q1256

最后 q q q 的长度 idx + 1 就是最长严格递增子序列的长度。但是 q q q 所存储的序列一般不是最短序列，另类的一种全为最小值的最长严格递增的乱序序列。

例如：
7 3 4 5 1 8 3 输出 ：1 4 5 8（保存了最长严格递增子序列的长度）
但是正确答案：3 4 5 8（由于 最小值 1 替代了 3）


代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int q[N], a[N], idx;

int find(int target, int range)
{
	int l = 0, r = range;
	while (l < r)
	{
		int mid = l + r >> 1;
		if (q[mid] >= target) r = mid;
		else l = mid + 1;
	}
	return l;
}
int main()
{
	int n;
	cin >> n;

	for (int i = 0; i < n; ++i) cin >> a[i];
	q[0] = a[0];
	for (int i = 1; i < n; ++i)
	{
		if (q[idx] < a[i]) q[++idx] = a[i];
		else q[find(a[i], idx)] = a[i];
	}
	cout << idx + 1 << endl;
	return 0;
}

扩展： 最长序列输出

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<vector>
using namespace std;

const int N = 1e3 + 10;
int q[N], a[N], pos[N], idx;

void print_path(int n)
{
	vector<int> path;
	for (int i = n - 1; i >= 0 && idx >= 0; --i)
	{
		if (pos[i] != idx) continue;
		path.push_back(a[i]);
		idx--;
	}
	for (int i = path.size() - 1; i >= 0; --i) cout << path[i] << ' ';
	cout << endl;
}
int binary_search(int target, int len)
{
	int l = 0, r = len;
	while (l < r)
	{
		int mid = l + (r - l) / 2;
		if (q[mid] >= target) r = mid;
		else l = mid + 1;
	}
	return l;
}
int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i) cin >> a[i];
	q[0] = a[0];
	for (int i = 1; i < n; ++i)
	{
		if (a[i] > q[idx])
		{
			q[++idx] = a[i];
			pos[i] = idx;
		}
		else
		{
			int t = binary_search(a[i], idx);
			q[t] = a[i];
			pos[i] = t;
		}
	}
	cout << idx + 1 << endl;
	print_path(n);
	return 0;
}

最长公共子序列

题目描述：
给定两个长度分别为 N N N 和 M M M 的字符串 A A A 和 B B B，求既是 A A A 的子序列又是 B B B 的子序列的字符串 长度最长 是多少。

输入格式：
第一行包含两个整数 N N N 和 M M M。

第二行包含一个长度为 N N N 的字符串，表示字符串 A A A。

第三行包含一个长度为 M M M 的字符串，表示字符串 B B B。

字符串均由小写字母构成。

输出格式：
输出一个整数，表示最大长度。

数据范围：
1 ≤ N , M ≤ 1000 1≤N,M≤1000 1≤N,M≤1000

输入样例：

4 5
acbd
abedc

输出样例：

3

算法思路

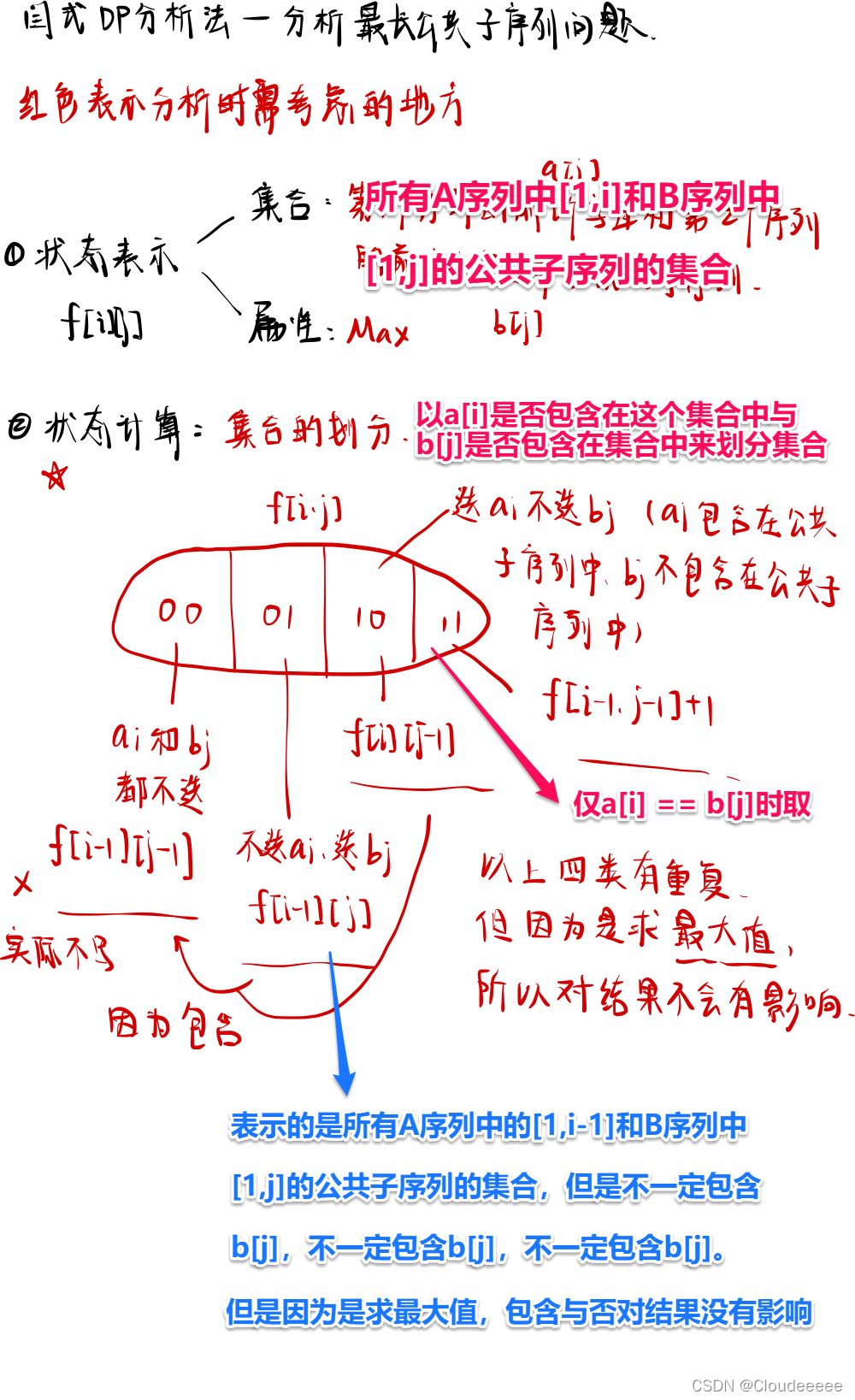
在这里插入图片描述


代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1010;
char a[N], b[N];
int f[N][N];

int main()
{
	int n, m;
	cin >> n >> m >> a + 1 >> b + 1;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
		{
			if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1] + 1;
			else f[i][j] = max(f[i - 1][j], f[i][j - 1]);
		}
	cout << f[n][m] << endl;
	return 0;
}

最短编辑距离

题目描述：
给定两个字符串 A A A 和 B B B，现在要将 A A A 经过若干操作变为 B B B，可进行的操作有：

  1. 删除–将字符串 A A A 中的某个字符删除。
  2. 插入–在字符串 A A A 的某个位置插入某个字符。
  3. 替换–将字符串 A A A 中的某个字符替换为另一个字符。

现在请你求出，将 A A A 变为 B B B 至少需要进行多少次操作。

输入格式：
第一行包含整数 n n n，表示字符串 A A A 的长度。

第二行包含一个长度为 n n n 的字符串 A A A。

第三行包含整数 m m m，表示字符串 B B B 的长度。

第四行包含一个长度为 m m m 的字符串 B B B。

字符串中均只包含大小写字母。

输出格式：
输出一个整数，表示最少操作次数。

数据范围：
1 ≤ n , m ≤ 1000 1≤n,m≤1000 1≤n,m≤1000

输入样例：

10 
AGTCTGACGC
11 
AGTAAGTAGGC

输出样例：

4

算法思路

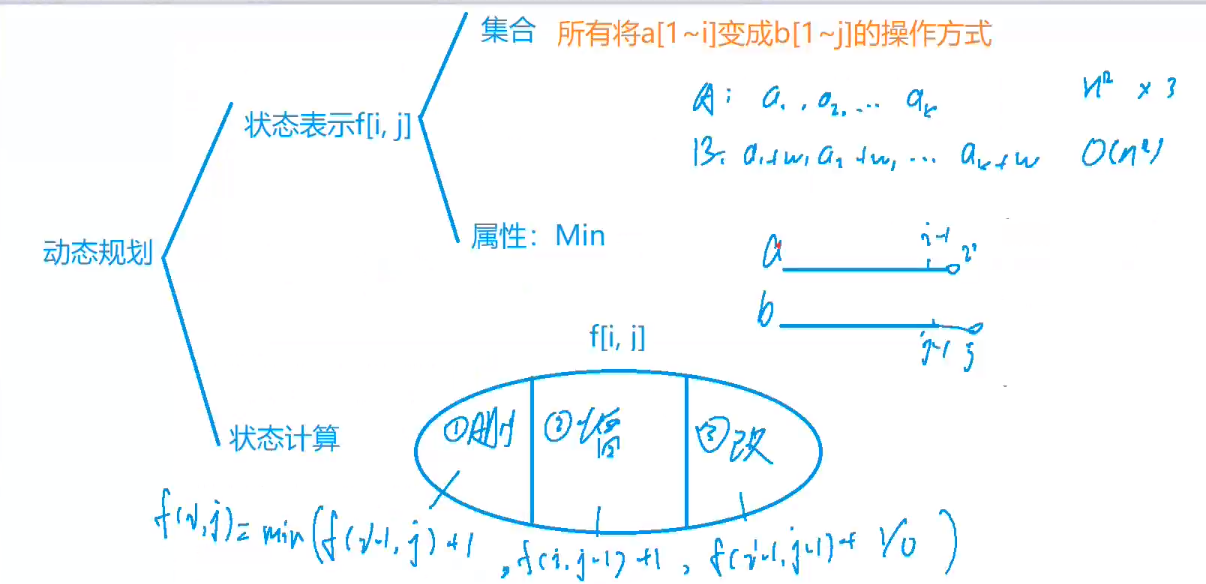
在这里插入图片描述

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1010;
int f[N][N];
char a[N], b[N];

int main()
{
	int n, m;
	cin >> n >> a + 1;
	cin >> m >> b + 1;
	for (int i = 0; i <= n; ++i) f[i][0] = i; // 提前赋值，避免边界问题
	for (int i = 0; i <= m; ++i) f[0][i] = i;
	
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
		{
			f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1; // 增和减的情况
			if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]); // 匹配完全的情况
			else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1); // 改的情况
		}
	cout << f[n][m] << endl;
	return 0;
}

编辑距离

题目描述：
给定 n n n 个长度不超过 10 10 10 的字符串以及 m m m 次询问，每次询问给出一个字符串和一个操作次数上限。

对于每次询问，请你求出给定的 n n n 个字符串中有多少个字符串可以在上限操作次数内经过操作变成询问给出的字符串。

每个对字符串进行的单个字符的插入、删除或替换算作一次操作。

输入格式：
第一行包含两个整数 n n n 和 m m m。

接下来 n n n 行，每行包含一个字符串，表示给定的字符串。

再接下来 m m m 行，每行包含一个字符串和一个整数，表示一次询问。

字符串中只包含小写字母，且长度均不超过 10 10 10。

输出格式：
输出共 m m m 行，每行输出一个整数作为结果，表示一次询问中满足条件的字符串个数。

数据范围：
1 ≤ n , m ≤ 1000 1≤n,m≤1000 1≤n,m≤1000

输入样例：

3 2
abc
acd
bcd
ab 1
acbd 2

输出样例：

1
3

代码实现

相当于对最短编辑距离的多次运用

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 15, M = 1010;
char str[M][N];
int f[N][N];
int n, m;

int edit_distance(char a[], char b[])
{
	int la = strlen(a + 1), lb = strlen(b + 1);
	for (int i = 0; i <= la; ++i) f[i][0] = i;
	for (int i = 0; i <= lb; ++i) f[0][i] = i;

	for (int i = 1; i <= la; ++i)
		for (int j = 1; j <= lb; ++j)
		{
			f[i][j] = min(f[i][j - 1], f[i - 1][j]) + 1;
			f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
		}
	return f[la][lb];
}
int main()
{
	cin >> n >> m;
	for (int i = 0; i < n; ++i) cin >> (str[i] + 1);
	while (m--)
	{
		int limit, res = 0;
		char a[N];
		cin >> a + 1 >> limit;
		for (int i = 0; i < n; ++i)
			if (edit_distance(str[i], a) <= limit) res++;
		cout << res << endl;
	}
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/964032.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2023蓝帽杯初赛

2023蓝帽杯初赛

比赛总结就是首先审题要仔细&#xff0c;确定题目意思再去找才不会找错。 内存取证vol工具的使用不够熟练 然后容易走进死胡同&#xff0c;如果一个软件不能得到答案可以换一个看看&#xff0c;说不定就有答案了。 还有服务器取证很生疏&#xff0c;还是要多花时间做点题 取…
阅读更多...
黑客之批处理编写

黑客之批处理编写

文章目录 一、批处理作用二、如何创建批处理三、批处理语法 一、批处理作用 自上而下成批的处理每一条命令&#xff0c;直到执行最后一条。这里的命令指的是DOS命令&#xff0c;在之前的【黑客常用DOS命令】博客中&#xff0c;我介绍了大量的常用DOS命令。不过我们之前输入命令…
阅读更多...
Lesson3-5:OpenCV图像处理---模版匹配和霍夫变换

Lesson3-5:OpenCV图像处理---模版匹配和霍夫变换

学习目标 掌握模板匹配的原理&#xff0c;能完成模板匹配的应用理解霍夫线变换的原理&#xff0c;了解霍夫圆检测知道使用OpenCV如何进行线和圆的检测 1 模板匹配 1.1 原理 所谓的模板匹配&#xff0c;就是在给定的图片中查找和模板最相似的区域&#xff0c;该算法的输入包括…
阅读更多...
C++之map，set，multimap，multiset的使用

C++之map，set，multimap，multiset的使用

map&#xff0c;set&#xff0c;multimap&#xff0c;multiset的使用 关联式容器键值对树形结构的关联式容器setset介绍set的使用set定义方式set各种操作函数 multiset mapmap的介绍map的使用insert函数find函数erase函数[ ]运算符重载map的迭代器遍历 multimap 关联式容器 在…
阅读更多...
ARM编程模型-状态模式

ARM编程模型-状态模式

ARM的两种工作状态 大部分的ARM处理器都实现了两种指令集&#xff0c;32位ARM指令集和16位Thumb指令集&#xff0c;看生成的机器码是32位的还是16位的 ARM v6引入了新的指令集Thumb-2,能够提供32位和16位的混合指令&#xff0c;在增强了灵活性的同时保持了代码的高密度。 ARM的…
阅读更多...
Linux基础学习2

Linux基础学习2

Linux基础学习2 popen函数 popen函数 https://blog.csdn.net/yzy1103203312/article/details/78483566 https://blog.csdn.net/xy1413_/article/details/127135608 典型用法&#xff1a; FILE * fp popen("ifconfig eth0", "r"); if (!fp) { fprintf…
阅读更多...
再谈IOS开发环境配置（2023-09-01 新）

再谈IOS开发环境配置（2023-09-01 新）

关于IOS的开发&#xff0c;需要配置证书、密钥、管理标识符、功能配置等等&#xff0c;很是繁杂&#xff0c;以前也配置过&#xff0c;这次因为重新购买了新的M1笔记本&#xff0c;准备重新配置下&#xff0c;顺便记录&#xff0c;以便查询。 如果要开发IOS&#xff0c;首先需要…
阅读更多...
2023高教社杯数学建模思路 - 案例：ID3-决策树分类算法

2023高教社杯数学建模思路 - 案例：ID3-决策树分类算法

文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 &#xff08;赛题出来以后第一时间在CSDN分享&#xff09; https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法&#xff0c;就是频繁模…
阅读更多...
JVM学习(一)--程序计数器

JVM学习(一)--程序计数器

作用&#xff1a;记住下一个jvm指令的执行地址 每一行java源代码&#xff0c;会被编译为多行jvm指令&#xff0c;上文所说的执行地址就是这里的0,3,4等 &#xff0c;由于执行访问特别频繁&#xff0c;程序计数器的底层是有寄存器来实现的 特点&#xff1a; 线程私有&#xff…
阅读更多...
爬虫进阶-反爬破解5（selenium的优势和点击操作+chrome的远程调试能力+通过Chrome隔离实现一台电脑登陆多个账号）

爬虫进阶-反爬破解5（selenium的优势和点击操作+chrome的远程调试能力+通过Chrome隔离实现一台电脑登陆多个账号）

目录 一、selenium的优势和点击操作 二、chrome的远程调试能力 三、通过Chrome隔离实现一台电脑登陆多个账号 一、selenium的优势和点击操作 1.环境搭建 工具&#xff1a;Chrome浏览器chromedriverselenium win用户&#xff1a;chromedriver.exe放在python.exe旁边 MacO…
阅读更多...
这段代码这么写有什么问题

这段代码这么写有什么问题

这段代码这么写有什么问题? List<String> baseRelList1 new ArrayList<>();epmPersonList.forEach(Obj ->{interviewBacklogMessageList.forEach(t ->{if (!Obj.equals(t.getPsnNum())){baseRelList1.add(Obj);}});});这段代码存在一个问题&#xff0c;即…
阅读更多...
transformer源码

transformer源码

1.传统RNN网络 每一层都需要上一层执行完才能执行 1.1 自注意力 在一句话中找到it_指代的是什么&#xff0c;它的上下文语境是什么&#xff1f; self-attetion计算 1.2 multi-header机制 1.3 堆叠多层self-attention&#xff0c;相当于再一次卷积 1.4 位置信息编码 1.5 残…
阅读更多...
unity 场景烘焙问题之模型UV有重叠

unity 场景烘焙问题之模型UV有重叠

问题现象&#xff1a;模型烘焙出来后&#xff0c;呈现黑色或布满脏斑&#xff0c;有可能是没有展UV&#xff0c;也有可能是UV重叠了 并且也会出现警告提示&#xff0c;如下图&#xff1a; 如果我们勾选了如下图,还在提示我们勾选&#xff0c;那可能就是 UV重叠了 解决方案 UV…
阅读更多...
C++：输出系统时间（及报错处理）

C++：输出系统时间（及报错处理）

#include <iostream> #include <ctime>using namespace std;int main() {// 基于当前系统的当前日期/时间time_t now time(0);cout << "1970 到目前经过秒数:" << now << endl;tm* ltm localtime(&now);// 输出 tm 结构的各个组…
阅读更多...
【微服务】一张图搞懂微服务架构设计

【微服务】一张图搞懂微服务架构设计

一张图搞懂微服务架构设计 1.前言2.流量入口 Nginx3.网关4.业务组件5.服务注册中心6.缓存和分布式锁7.数据持久层8.结构型数据存储9.消息中间件10.日志收集11.任务调度中心12.分布式对象存储 1.前言 当前&#xff0c;微服务架构在很多公司都已经落地实施了&#xff0c;下面用一…
阅读更多...
气象科普丨气象站的分类与应用

气象科普丨气象站的分类与应用

气象站是一种用于收集、分析和处理气象数据的设备。根据不同的应用场景和监测需求&#xff0c;气象站可以分为以下几类&#xff1a; 一、农业气象站 农业气象站是专门为农业生产服务的气象站&#xff0c;主要监测土壤温度、土壤湿度等参数&#xff0c;为农业生产提供科学依据…
阅读更多...
高效率、高质量的DMG映像制作：DMG Canvas for mac，助你轻松实现

高效率、高质量的DMG映像制作：DMG Canvas for mac，助你轻松实现

如果你是一位开发者或企业用户&#xff0c;你一定知道DMG磁盘映像文件在分发应用程序或文件时的重要性。DMG磁盘映像文件可以让用户轻松地创建磁盘映像&#xff0c;并将其挂载到Mac电脑上&#xff0c;从而方便地安装或使用应用程序或文件。 然而&#xff0c;传统的DMG磁盘映像…
阅读更多...
数学之美 — 1

数学之美 — 1

为什么你会想和他人共享那些美丽的事物呢&#xff1f;因为这会让他&#xff08;她&#xff09;感到愉悦&#xff0c;也能让你在分享的过程中重新欣赏一次事物的美。 ——David Blackwell 1、感官之美&#xff0c;对于那些有规律的事物&#xff0c;你可以利用自己的视觉、触觉、…
阅读更多...
CodeBlocks20.03配置wxWidgets

CodeBlocks20.03配置wxWidgets

背景 - 现在是2023年 1. 很多年前&#xff0c;下载使用CodeBlocks就发现里面有自带的wxWidgets Project的项目&#xff0c;然而一路Next下去出来的程序根本就不能运行&#xff0c;心有不甘&#xff1b; 2. 前几年&#xff0c;用python做小工具的时候&#xff0c;界面用的wxPy…
阅读更多...
AutoSAR CP 飞阅TIME

AutoSAR CP 飞阅TIME

目录 什么是autosar autosar 做了什么 Foundation、CP、AP CLASSIC PLATFORM &#xff08;CP&#xff09; ADAPTIVE PLATFORM 基于autosar 开发 SWC Port Runnables RTE BSW MCAL CDD I/O Hardware Abstraction Communication Hardware Abstraction Memory Har…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023