题1:岛屿周长
给定一个 row x col 的二维网格地图 grid ,其中:gridi = 1 表示陆地, gridi = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例:

思路:
一块土地原则上会带来4个周长,但岛上的土地存在接壤,会减掉2个边长。
所以,总周长=4*土地个数-2*接壤边的条数
遍历矩阵,遍历到土地,就land++,如果它的右边或下边也是土地,则border++,便遍历结束后代入公式即可。

Code:
int islandPerimeter(int** grid, int gridSize, int* gridColSize){
int land=0;//土地的块数
int broader=0;//土地接壤的块数
for(int i=0;i<gridSize;i++)
{
for(int j=0;j<gridColSize[i];j++)
{
if(grid[i][j])
{
land++;//如果遍历到土地,那么就land++
if(i<gridSize-1&&grid[i+1][j])//如果土地的下方也是土地,那么broader++
{
broader++;
}
if(j<gridColSize[i]-1&&grid[i][j+1])//如果土地的右方也是土地,那么broader++
{
broader++;
}
}
}
}
int result=4*land-2*broader;//一块土地有四条边,一个土地每接壤了一块土地,就要少两条边
//所以总边数=4*土地块数-2*接壤土地块数
return result;
}题2:岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
思路:
本题我们可以采用递归算法来实现,遍历矩阵,找到陆地后,开始递归查找当前位置的上下左右四个方向是否也为陆地。在这过程中要注意的是,每访问一块陆地后要将其更新为'0',防止重复访问,产生死循环。
Code:
class Solution {
public:
void dfs(vector<vector<char>>& grid,int i,int j)
{
int n=grid.size();
int m=grid[0].size();
//访问过就更新为'0'
grid[i][j]='0';
//继续判断上下左右四个方向是否是岛屿
if(i-1>=0 && grid[i-1][j]=='1') dfs(grid,i-1,j);
if(i+1<n && grid[i+1][j]=='1') dfs(grid,i+1,j);
if(j-1>=0 && grid[i][j-1]=='1') dfs(grid,i,j-1);
if(j+1<m && grid[i][j+1]=='1') dfs(grid,i,j+1);
}
int numIslands(vector<vector<char>>& grid) {
int n=grid.size();
int m=grid[0].size();
int num=0;//记录岛屿个数
//遍历矩阵
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
//如果当前位置为陆地,也就是为'1',则找它的上下左右相连的陆地
if(grid[i][j]=='1')
{
dfs(grid,i,j);
//岛屿数量加1
num++;
}
}
}
return num;
}
};题3:统计子岛屿
你两个 m x n 的二进制矩阵 grid1 和 grid2 ,它们只包含 0 (表示水域)和 1 (表示陆地)。一个 岛屿 是由 四个方向 (水平或者竖直)上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。
如果 grid2 的一个岛屿,被 grid1 的一个岛屿 完全 包含,也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含,那么我们称 grid2 中的这个岛屿为 子岛屿 。
请你返回 grid2 中 子岛屿 的 数目 。
示例:
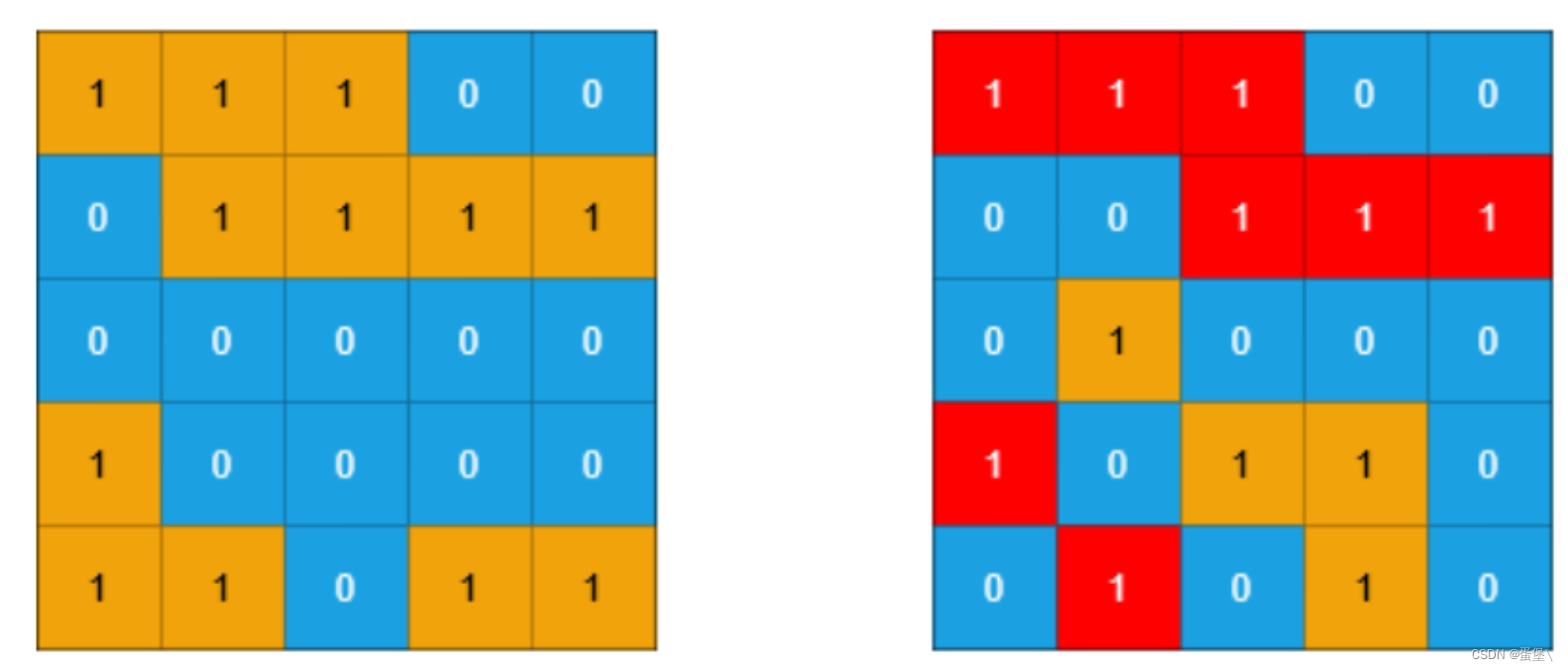
输入:grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
输出:3
解释:如上图所示,左边为 grid1 ,右边为 grid2 。
grid2 中标红的 1 区域是子岛屿,总共有 3 个子岛屿。
思路:
1.首先要明确子岛屿的定义:grid2 的一个岛屿必须被 grid1 的一个岛屿 完全 包含。
2.我们采用递归算法来实现本题
3.在写递归条件时,我们需要考虑的是,当遇到下标越界或是土地2的一个岛屿已经结束(也就是grid2[i][j]!=1)时,说明当前的这个子岛屿已经判断完毕,return true
4.每访问一个位置,就要将当前位置变成不是陆地,这里我设置成2,为了防止出现死循环,设置过之后,访问过的位置不会再次被访问
5.设置一个标记,用来标记当前是否为子岛屿
6.每次都要判断上下左右四个方向是否是陆地,且满足被包含在土地1的岛屿中
Code:
class Solution {
public:
//坐标的偏移量(上下左右四个方向)
int dx[4]={0,0,-1,1};
int dy[4]={-1,1,0,0};
bool dfs(vector<vector<int>>& grid1, vector<vector<int>>& grid2,int i,int j)
{
int n=grid1.size();
int m=grid1[0].size();
//如果不是陆地,或越界,返回true
if(i>=n||i<0||j>=m||j<0||grid2[i][j]!=1) return true;
//访问过的位置置为2,防止出现死循环
grid2[i][j]=2;
//设置标记flag,初始为true
bool flag=true;
//如果土地1当前位置不是陆地,则将flag置为flase,在最后统一返回,不能现在直接return,不然会导致有些岛屿没有判断到
if(grid1[i][j]==0) flag=false;
//开始找上下左右四个方向
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
//这里flag必须两个条件相与,如果上一轮flag为false,那么说明土地1的岛屿没有完全包含土地2的岛屿,即使此时两块土地的位置都为1,也不符合题意,flag仍然为false
flag=dfs(grid1,grid2,x,y) && flag;
}
return flag;
}
int countSubIslands(vector<vector<int>>& grid1, vector<vector<int>>& grid2) {
int n=grid1.size();
int m=grid1[0].size();
int res=0;//记录子岛屿的个数
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
//如果当前土地2的位置是陆地,同时土地1的位置也是陆地,才能进入递归
//因为我们在递归中,设置为只要不是陆地,那么当前位置就是子岛屿,所以进入递归的前提条件就是当前位置必须是陆地
if(grid2[i][j]==1 && grid1[i][j]==1)
{
if(dfs(grid1,grid2,i,j))
res++;
}
}
}
return res;
}
};