一、说明

在这篇文章中，我们讨论了常α MC 方法和 TD（0）方法之间的区别，并比较了它们在随机游走任务中的性能。TD方法在本文的所有测试中都覆盖了MC方法，因此将TD视为强化学习任务的方法是更可取的选择。

二、方法库介绍

蒙特卡洛（MC）和时间差分（TD）方法都是强化学习领域的基础技术;他们根据与环境交互的经验而不是环境的模型来解决预测问题。但是，TD方法是MC方法和动态规划（DP）的组合，因此在更新规则，自举和偏差/方差方面与MC方法不同。在大多数情况下，TD方法也被证明具有比MC更好的性能和更快的收敛。

在这篇文章中，我们将在简单的网格环境和更全面的随机游走 [0] 环境中比较 TD（2）和常数α MC 方法。希望这篇文章可以帮助对强化学习感兴趣的读者更好地了解每种方法如何更新状态值函数，以及它们在相同的测试环境中的性能有何不同。

我们将在 Python 中实现算法和比较，本文中使用的库如下：

python==3.9.16
numpy==1.24.3
matplotlib==3.7.1

三、TD和MC的区别

3.1 引入TD（0）和常α MC

常α MC 方法是一种常规 MC 方法，具有恒定的步长参数α，此常量参数有助于使值估计对最近的体验更敏感。在实践中，α值的选择取决于稳定性和适应性之间的权衡。以下是 MC 方法在时间 t 更新状态值函数的公式：

TD（0）是TD（λ）的一个特例，它只领先一步，是最简单的TD学习形式。此方法使用 TD 误差更新状态值函数，TD 误差是状态的估计值与奖励之间的差值加上下一个状态的估计值。常量步长参数α的工作方式与上述 MC 方法相同。以下是在时间 t 更新状态值函数的 TD（0）方程：

一般来说，MC和TD方法之间的差异发生在三个方面：

更新规则：MC 方法仅在剧集结束后更新值;如果剧集很长，这会减慢程序的速度，或者在根本没有剧集的持续任务中，这可能会有问题。相反，TD方法在每个时间步更新值估计值;这是在线学习，在连续任务中特别有用。
自举：强化学习中的术语“自举”是指根据其他价值估计更新价值估计。TD（0）方法的更新基于以下状态的值，因此它是一种引导方法;相反，MC 不使用引导，因为它直接从返回值（G）更新值。
偏差/方差：MC方法是无偏的，因为它们通过权衡观察到的实际回报来估计值，而无需在发作期间进行估计;然而，MC 方法具有很高的方差，尤其是在样本数量较少时。相反，TD方法存在偏差，因为它们使用自举，并且偏差可能会根据实际实现而变化;TD方法的方差较低，因为它使用即时奖励加上对下一个状态的估计，从而消除了奖励和行动随机性引起的波动。

3.2 在简单的网格世界设置上评估TD（0）和恒定α MC

为了使它们的差异更加直接，我们可以设置一个简单的 Gridworld 测试环境，其中包含两个固定轨迹，在设置上运行这两种算法直到收敛，并检查它们如何以不同的方式更新值。

首先，我们可以使用以下代码设置测试环境：

# Environment setup
def get_env():
    grid = np.zeros(shape=(6, 6), dtype=float)
    grid[:, -1] = -1
    grid[2, -1] = 1
    return grid

# Pre-defined paths
def get_paths():
    path_1 = [(4, 0), (4, 1), (3, 1), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5)]
    path_2 = [(5, 3), (4, 3), (3, 3), (2, 3), (1, 3), (0, 3), (0, 4), (0, 5)]
    return path_1, path_2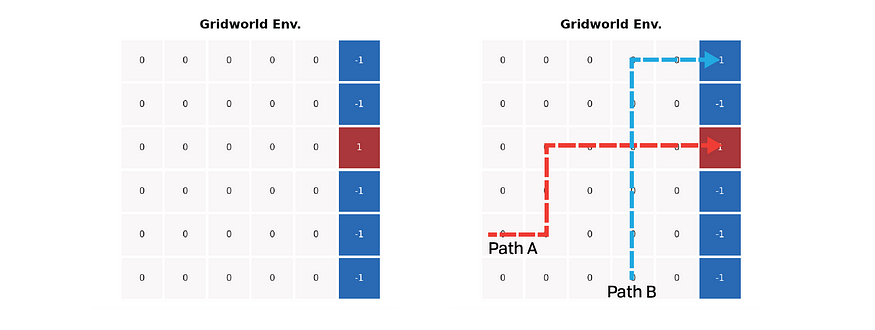

上图显示了一个简单的网格世界环境设置。所有彩色单元格都代表终端状态;代理在进入红色单元格时获得 +1 奖励，但在进入蓝色单元格时获得 -1 奖励。网格上的所有其他步骤返回奖励为零。上图右图标记了两条预设路径：一条到达蓝色单元格，另一条停止在红色单元格处;路径的交集有助于最大化两种方法之间的值差异。

然后，我们可以使用上一节中的方程来评估环境。我们不对回报或估计进行折扣，并将α设置为较小的值 1e-3。当值增量的绝对总和低于阈值 1e-3 时，我们认为值已收敛。

# Monte Carlo Evaluation
def mc_sweep():
    env = get_env()
    V = np.zeros_like(env)
    alpha = 1e-3
    trajs = get_paths()
    while True:
        increment = np.zeros_like(V)
        for traj in trajs:
            G = env[traj[-1][0], traj[-1][1]]
            for i in range(len(traj) - 2, -1, -1):
                row, col = traj[i]
                increment[row, col] += G - V[row, col]
        increment *= alpha
        if np.abs(increment).sum() < 1e-3:
            break
        V += increment
    return V


# TD evaluation
def td_sweep():
    env = get_env()
    V = np.zeros_like(env)
    alpha = 1e-3
    trajs = get_paths()
    while True:
        increment = np.zeros_like(V)
        for traj in trajs:
            for i in range(len(traj) - 1):
                curr_row, curr_col = traj[i]
                next_row, next_col = traj[i + 1]
                increment[curr_row, curr_col] += (
                    env[next_row, next_col]
                    + V[next_row, next_col]
                    - V[curr_row, curr_col]
                )
        increment *= alpha
        if np.abs(increment).sum() < 1e-3:
            break
        V += increment
    return V


if __name__ == "__main__":
    env = get_env()
    V_mc = mc_sweep()
    V_td = td_sweep()
    V_mc[:, -1] = env[:, -1]
    V_td[:, -1] = env[:, -1]
    titles = ["Gridworld Env.", "Monte Carlo", "Temporal-Difference"]
    plt.figure(figsize=(9, 3), dpi=300)
    for i, V in enumerate([env, V_mc, V_td]):
        ax = plt.subplot(1, 3, i + 1)
        ax.set_title(titles[i], fontdict={"fontsize": 7, "fontweight": "bold"})
        ax = sns.heatmap(
            V,
            linewidths=1,
            annot=True,
            annot_kws={"fontsize": 5},
            cmap="vlag",
            square=True,
            cbar=False,
            xticklabels=False,
            yticklabels=False,
        )
    plt.show()

评估结果如下：

这两种算法估计值的不同方式在上图中变得非常明显。MC 方法忠实于路径的返回，因此每个路径上的值直接表示其结束方式。尽管如此，TD方法提供了更好的预测，特别是在蓝色路径上 - 交叉点前蓝色路径上的值也表明到达红细胞的可能性。

考虑到这个最小的情况，我们准备转到一个更复杂的示例，并尝试找出两种方法之间的性能差异。

四、随机游走任务

随机游走任务是Sutton等人提出的一个简单的马尔可夫奖励过程，用于TD和MC预测目的[2]，如下图所示。在此任务中，代理从中心节点 C 开始。代理在每个节点上以相等的概率向右或向左走一步。链的两端有两种终端状态。进入左端的奖励是0，进入右端的奖励是+1。终止前的所有步骤都会产生 0 的奖励。

我们可以使用以下代码来创建随机漫游环境：

import numpy as np

# Using node to represent the states and the connection between each pair
class Node:
    def __init__(self, val: str):
        self.value = val
        self.right = None
        self.left = None
        self.r_reward = 0  # the reward of stepping right
        self.l_reward = 0  # the reward of stepping right

    def __eq__(self, other_val) -> bool:
        return self.value == other_val

    def __repr__(self) -> str:
        return f"Node {self.value}"


# Build the Random Walk environment
class RandomWalk:
    def __init__(self):
        self.state_space = ["A", "B", "C", "D", "E"]
        # We need to make the mapping start from 1 and reserve 0 for the terminal state
        self.state_idx_map = {
            letter: idx + 1 for idx, letter in enumerate(self.state_space)
        }
        self.initial_state = "C"
        self.initial_idx = self.state_idx_map[self.initial_state]
        # Build environment as a linked list
        self.nodes = self.build_env()
        self.reset()

    def step(self, action: int) -> tuple:
        assert action in [0, 1], "Action should be 0 or 1"

        if action == 0:
            reward = self.state.l_reward
            next_state = self.state_idx_map[self.state.value] - 1
            self.state = self.state.left
        else:
            reward = self.state.r_reward
            next_state = self.state_idx_map[self.state.value] + 1
            self.state = self.state.right

        terminated = False if self.state else True
        return next_state, reward, terminated

    # reset the state to the initial node
    def reset(self):
        self.state = self.nodes
        while self.state != self.initial_state:
            self.state = self.state.right

    # building the random walk environment as a linked list
    def build_env(self) -> Node:
        values = self.state_space
        head = Node(values[0])
        builder = head
        prev = None
        for i, val in enumerate(values):
            next_node = None if i == len(values) - 1 else Node(values[i + 1])
            if not next_node:
                builder.r_reward = 1

            builder.left = prev
            builder.right = next_node
            prev = builder
            builder = next_node
        return head

=====Test: checking environment setup=====

Links:        None ← Node A → Node B
Reward:          0 ← Node A → 0

Links:      Node A ← Node B → Node C
Reward:          0 ← Node B → 0

Links:      Node B ← Node C → Node D
Reward:          0 ← Node C → 0

Links:      Node C ← Node D → Node E
Reward:          0 ← Node D → 0

Links:      Node D ← Node E → None
Reward:          0 ← Node E → 1

随机策略下环境每个节点的真实值为 [1/6， 2/6， 3/6， 4/6， 5/6]。该值是通过使用贝拉姆方程进行策略评估计算的：

我们在这里的任务是找出两种算法估计的值与真实值的接近程度;我们可以任意假设该算法产生的值函数更接近真值函数，由平均均方根误差（RMS）测量，表明性能更好。

五、TD（0）和常数 MC 在随机游走中的性能

5.1 算法

准备好环境后，我们可以开始在随机游走环境中运行这两种方法并比较它们的性能。首先让我们看一下这两种算法：

如前所述，MC 方法应等到剧集结束再更新轨迹尾部的值，而 TD 方法则增量更新值。这种差异在初始化状态值函数时带来了一个技巧：在 MC 中，状态值函数不包括终端状态，而在 TD（0）中，函数应包含值为 0 的终端状态，因为 TD（0）方法总是在剧集结束之前领先一步。

5.2 实现

此实现中的α参数选择引用了书中提出的参数 [2];MC方法的参数为[0.01， 0.02， 0.03， 0.04]，TD方法的参数为[0.05， 0.10， 0.15]。我想知道为什么作者没有在两种算法上选择相同的参数集，直到我运行带有TD参数的MD方法：TD参数对于MC方法来说太高了，因此无法揭示MC的最佳性能。因此，我们将在参数扫描中坚持本书的设置。现在，让我们运行这两种算法来找出它们在随机游走设置中的性能。

5.3 结果

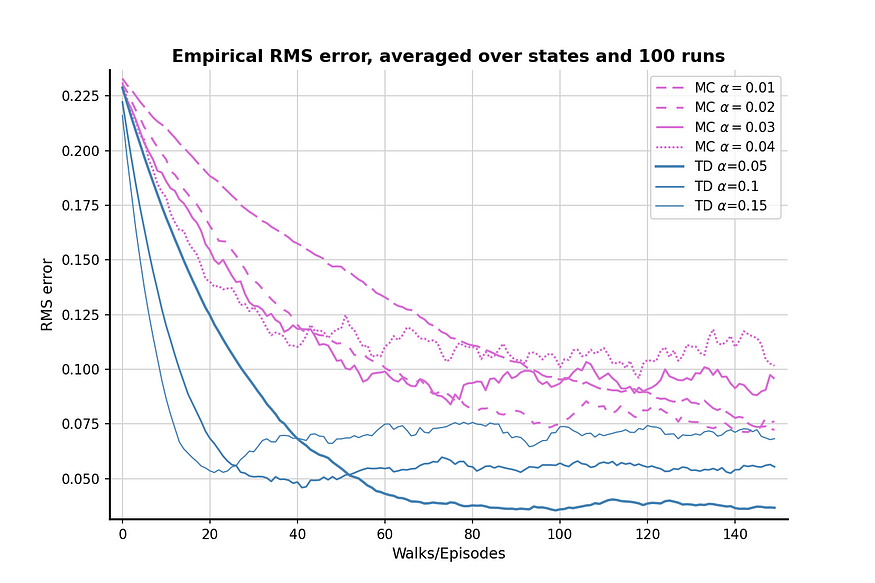
100 次比较后的结果如上图所示。TD方法通常比MC方法产生更好的值估计，并且α = 0.05的TD可以非常接近真实值。该图还显示，与TD方法相比，MC方法具有更高的方差，因为兰花线的波动大于钢蓝线。

值得注意的是，对于这两种算法，当α（相对）高时，RMS损耗首先下降，然后再次上升。这种现象是由于值初始化和α值的综合效应造成的。我们初始化了一个相对较高的值 0.5，它高于节点 A 和 B 的真实值。由于随机策略有 50% 的机会选择“错误”的步骤，从而使代理远离正确的终端状态，因此较高的α值也会强调错误的步骤并使结果远离真实值。

现在让我们尝试将初始值减小到 0.1 并再次运行比较，看看问题是否缓解：

较低的初始值显然有助于缓解问题;没有明显的“下降，然后上升”效果。然而，较低初始值的副作用是学习效率较低，因为 RMS 损失在 0 次发作后永远不会低于 05.150。因此，在初始值、参数和算法性能之间进行权衡。

六、批量训练

我想在这篇文章中提出的最后一点是两种算法的批量训练的比较。

考虑我们面临以下情况：我们在随机游走任务上只积累了有限数量的经验，或者由于时间和计算的限制，我们只能运行一定数量的剧集。提出批量更新的想法[2]是为了通过充分利用现有轨迹来处理这种情况。

批量训练的想法是反复更新一批轨迹上的值，直到值收敛到答案。只有在完全处理所有批处理体验后，才会更新这些值。让我们在随机游走环境中实现两种算法的批量训练，看看 TD 方法是否仍然比 MC 方法表现更好。

6.1 结果

批量训练的结果表明，在经验有限的情况下，TD方法仍然比MC方法做得更好，两种算法的性能差距相当明显。

七、结论

在这篇文章中，我们讨论了常α MC 方法和 TD（0）方法之间的区别，并比较了它们在随机游走任务中的性能。TD方法在本文的所有测试中都覆盖了MC方法，因此将TD视为强化学习任务的方法是更可取的选择。然而，这并不意味着TD总是比MC更好，因为后者有一个最明显的优势：没有偏见。如果我们面对的任务不能容忍偏见，那么 MC 可能是更好的选择;否则，TD可以更好地处理一般情况。