🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝

📣系列专栏 - 机器学习【ML】自然语言处理【NLP】深度学习【DL】

🖍foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟👋

文章目录

创建窗口数据集

创建时间序列数据集的窗口版本

创建和训练 DNN 以拟合序列数据

评估 DNN 的结果

探索整体预测

调整学习率

使用 Keras Tuner 探索超参数调整

概括

第9章介绍了序列数据和时间序列的属性，包括季节性、趋势、自相关和噪声。您创建了一个用于预测的合成序列，并探索了如何进行基本统计预测。在接下来的几章中，您将学习如何使用 ML 进行预测。但是在开始创建模型之前，您需要了解如何构建用于训练预测模型的时间序列数据，方法是创建我们称之为 窗口数据集。

至要了解为什么需要这样做，请考虑您在第 9 章中创建的时间序列。您可以在图 10-1中看到它的图。

图 10-1。合成时间序列

如果在任何时候您想预测时间t的值，您需要将其预测为时间t之前的值的函数。例如，假设您要预测时间序列在时间步长 1,200 处的值作为其前面 30 个值的函数。在这种情况下，从时间步长 1,170 到 1,199 的值将确定时间步长 1,200 的值，如图 10-2所示。

图 10-2。影响预测的先前值

现在这看起来很熟悉：您可以将 1,170–1,199 的值视为您的特征，将 1,200 的值视为您的特征标签。如果你可以让你的数据集进入这样一种情况，你有一定数量的值作为特征，下一个作为标签，并且你对数据集中的每个已知值都这样做，你最终会得到一组相当不错的可用于训练模型的特征和标签。

在对第 9 章的时间序列数据集执行此操作之前，让我们创建一个非常简单的数据集，该数据集具有所有相同的属性，但数据量要少得多。

创建窗口数据集

这 tf.data库包含许多可用于操作数据的 API。您可以使用这些创建包含数字 0-9 的基本数据集，模拟时间序列。然后，您将把它变成窗口数据集的开始。这是代码：

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(5))
for window in dataset:
    print(window.numpy())

首先，它使用范围创建数据集，这只是使数据集包含值 0 到n – 1，其中n在本例中为 10。

接下来，调用 dataset.window并传递5指定的参数将数据集拆分为五个项目的窗口。指定shift=1会导致每个窗口从前一个窗口移动一个位置：第一个窗口将包含从 0 开始的五个项目，下一个窗口将包含从 1 开始的五个项目，等等。设置drop_remainder为True指定一旦它到达接近数据集末尾的点，在该点窗口将小于所需的五个大小，它们应该被删除。

给定窗口定义，可以进行拆分数据集的过程。你用 flat_map函数，在本例中请求一批五个窗口。

运行这段代码将得到以下结果：

[0 1 2 3 4]
[1 2 3 4 5]
[2 3 4 5 6]
[3 4 5 6 7]
[4 5 6 7 8]
[5 6 7 8 9]

但是之前您已经看到我们想要由此制作训练数据，其中有n 个值定义一个特征，随后的值给出一个标签。您可以通过添加另一个 lambda 函数来完成此操作，该函数将每个窗口拆分为最后一个值之前的所有内容，然后是最后一个值。这给出了一个x和一个y数据集，如下所示：

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(5))
dataset = dataset.map(lambda window: (window[:-1], window[-1:]))
for x,y in dataset:
    print(x.numpy(), y.numpy())

结果现在符合您的预期。窗口中的前四个值可以被认为是特征，随后的值是标签：

[0 1 2 3] [4]
[1 2 3 4] [5]
[2 3 4 5] [6]
[3 4 5 6] [7]
[4 5 6 7] [8]
[5 6 7 8] [9]

而且因为这是一个数据集，它还可以支持通过洗牌和批处理拉姆达函数。在这里，它被洗牌并以 2 的批大小进行批处理：

dataset = tf.data.Dataset.range(10)
dataset = dataset.window(5, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(5))
dataset = dataset.map(lambda window: (window[:-1], window[-1:]))
dataset = dataset.shuffle(buffer_size=10)
dataset = dataset.batch(2).prefetch(1)
for x,y in dataset:
    print("x = ", x.numpy())
    print("y = ", y.numpy())

结果表明，第一批有两组x（分别从 2 和 3 开始）及其标签，第二批有两组x（分别从 1 和 5 开始）及其标签，依此类推：

x =  [[2 3 4 5]
 [3 4 5 6]]
y =  [[6]
 [7]]

x =  [[1 2 3 4]
 [5 6 7 8]]
y =  [[5]
 [9]]

x =  [[0 1 2 3]
 [4 5 6 7]]
y =  [[4]
 [8]]

使用这种技术，您现在可以将任何时间序列数据集转换为神经网络的一组训练数据。在下一节中，您将探讨如何从第 9 章中获取合成数据并从中创建训练集。从那里开始，您将继续创建一个简单的 DNN，该 DNN 根据此数据进行训练并可用于预测未来值。

创建时间序列数据集的窗口版本

作为回顾一下，这是上一章中用于创建合成时间序列数据集的代码：

def trend(time, slope=0):
    return slope * time

def seasonal_pattern(season_time):
    return np.where(season_time < 0.4,
                    np.cos(season_time * 2 * np.pi),
                    1 / np.exp(3 * season_time))

def seasonality(time, period, amplitude=1, phase=0):
    season_time = ((time + phase) % period) / period
    return amplitude * seasonal_pattern(season_time)

def noise(time, noise_level=1, seed=None):
    rnd = np.random.RandomState(seed)
    return rnd.randn(len(time)) * noise_level

time = np.arange(4 * 365 + 1, dtype="float32")
series = trend(time, 0.1)
baseline = 10
amplitude = 20
slope = 0.09
noise_level = 5

series = baseline + trend(time, slope) 
series += seasonality(time, period=365, amplitude=amplitude)
series += noise(time, noise_level, seed=42)

这将创建一个如图 10-1 所示的时间序列。如果您想更改它，请随意调整各种常量的值。

获得系列后，您可以使用类似于上一节中的代码将其转换为窗口数据集。在这里，它被定义为一个独立的函数：

def windowed_dataset(series, window_size, 
                      batch_size, shuffle_buffer):
    dataset = tf.data.Dataset.from_tensor_slices(series)
    dataset = dataset.window(window_size + 1, shift=1, 
                              drop_remainder=True)
    dataset = dataset.flat_map(lambda window: 
                                 window.batch(window_size + 1))
    dataset = dataset.shuffle(shuffle_buffer).map(
                             lambda window: 
                                 (window[:-1], window[-1]))
    dataset = dataset.batch(batch_size).prefetch(1)
    return dataset

请注意，它使用的from_tensor_slices方法tf.data.Dataset，它允许您将系列转换为Dataset. 您可以在TensorFlow 文档中了解有关此方法的更多信息。

现在，要获得训练就绪的数据集，您只需使用以下代码即可。首先将系列分成训练和验证数据集，然后指定窗口大小、批量大小和随机缓冲区大小等详细信息：

split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
window_size = 20
batch_size = 32
shuffle_buffer_size = 1000
dataset = windowed_dataset(x_train, window_size, batch_size, 
                           shuffle_buffer_size)

现在要记住的重要一点是你的数据是一个tf.data.Dataset，所以它可以很容易地model.fit作为一个参数传递给它并tf.keras会处理剩下的事情。

如果您想检查数据的外观，可以使用如下代码：

dataset = windowed_dataset(series, window_size, 1, shuffle_buffer_size)
for feature, label in dataset.take(1):
    print(feature)
    print(label)

这里将batch_size设置为1，只是为了使结果更具可读性。您最终会得到这样的输出，其中批处理中包含一组数据：

tf.Tensor(
[[75.38214  66.902626 76.656364 71.96795  71.373764 76.881065 75.62607
  71.67851  79.358665 68.235466 76.79933  76.764114 72.32991  75.58744
  67.780426 78.73544  73.270195 71.66057  79.59881  70.9117  ]], 
  shape=(1, 20), dtype=float32)
tf.Tensor([67.47085], shape=(1,), dtype=float32)

第一批数字是特征。我们将窗口大小设置为 20，因此它是一个1 × 20的张量。第二个数字是标签（在本例中为 67.47085），模型将尝试将特征拟合到该标签。您将在下一节中看到它是如何工作的。

创建和训练 DNN 以拟合序列数据

现在如果您拥有 a 中的数据，那么在其中tf.data.Dataset创建神经网络模型tf.keras就变得非常简单。让我们首先探索一个简单的 DNN，如下所示：

dataset = windowed_dataset(series, window_size, 
                            batch_size, shuffle_buffer_size)

model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(10, input_shape=[window_size], 
                           activation="relu"), 
    tf.keras.layers.Dense(10, activation="relu"), 
    tf.keras.layers.Dense(1)
])

这是一个超级简单的模型，有两个密集层，第一个接受输入形状，window_size然后输出层将包含预测值。

和以前一样，该模型使用损失函数和优化器进行编译。在在这种情况下，损失函数指定为mse，它代表均方误差，常用于回归问题（这最终归结为！）。为了优化器sgd（随机梯度下降）非常适合。我不会在本书中详细介绍这些类型的函数，但任何关于机器学习的好资源都会教你它们——Andrew Ng 在 Coursera 上开创性的深度学习专业化是一个很好的起点。SGD 采用学习率 ( lr) 和动量参数，这些参数调整优化器的学习方式。每个数据集都是不同的，所以最好有控制权。在下一节中，您将看到如何找出最佳值，但现在，只需像这样设置它们：

model.compile(loss="mse",optimizer=tf.keras.optimizers.SGD(
                                                          lr=1e-6, 
                                                          momentum=0.9))

然后，训练就变得像调用一样简单model.fit，将您的数据集传递给它，并指定要训练的时期数：

model.fit(dataset,epochs=100,verbose=1)

在训练时，您会看到损失函数报告的数字开始很高，但会稳步下降。这是前 10 个时期的结果：

Epoch 1/100
45/45 [==============================] - 1s 15ms/step - loss: 898.6162
Epoch 2/100
45/45 [==============================] - 0s 8ms/step - loss: 52.9352
Epoch 3/100
45/45 [==============================] - 0s 8ms/step - loss: 49.9154
Epoch 4/100
45/45 [==============================] - 0s 7ms/step - loss: 49.8471
Epoch 5/100
45/45 [==============================] - 0s 7ms/step - loss: 48.9934
Epoch 6/100
45/45 [==============================] - 0s 7ms/step - loss: 49.7624
Epoch 7/100
45/45 [==============================] - 0s 8ms/step - loss: 48.3613
Epoch 8/100
45/45 [==============================] - 0s 9ms/step - loss: 49.8874
Epoch 9/100
45/45 [==============================] - 0s 8ms/step - loss: 47.1426
Epoch 10/100
45/45 [==============================] - 0s 8ms/step - loss: 47.5133

评估 DNN 的结果

一次你有一个训练有素的 DNN，你可以开始用它进行预测。但请记住，您有一个窗口数据集，因此，对给定点的预测是基于它之前一定数量的时间步长的值。

换句话说，由于您的数据位于名为的列表中series，要预测一个值，您必须将模型值从时间t传递到时间t + window_size。然后它将为您提供下一个时间步长的预测值。

例如，如果您想要预测时间步长 1,020 的值，您可以获取时间步长 1,000 到 1,019 的值，并使用它们来预测序列中的下一个值。要获取这些值，您可以使用以下代码（请注意，您将其指定为series[1000:1020]，而不是series[1000:1019]！）：

print(series[1000:1020])

然后，要获取第 1,020 步的值，您只需series[1020]像这样使用：

print(series[1020])

要获得对该数据点的预测，然后将系列传递给model.predict. 但是请注意，为了保持输入形状一致，您需要一个[np.newaxis]，如下所示：

print(model.predict(series[1000:1020][np.newaxis]))

或者，如果你想要更通用的代码，你可以使用这个：

print(series[start_point:start_point+window_size])
print(series[start_point+window_size])
print(model.predict(
      series[start_point:start_point+window_size][np.newaxis]))

请注意，所有这些都假设窗口大小为 20 个数据点，这非常小。因此，您的模型可能会缺乏一些准确性。如果您想尝试不同的窗口大小，则需要通过再次调用该windowed_dataset函数重新格式化数据集，然后重新训练模型。

以下是该数据集以 1,000 为起点并预测下一个值时的输出：

[109.170746 106.86935  102.61668   99.15634  105.95478  104.503876
 107.08533  105.858284 108.00339  100.15279  109.4894   103.96404
 113.426094  99.67773  111.87749  104.26137  100.08899  101.00105
 101.893265 105.69048 ]

106.258606

[[105.36248]]

第一个张量包含值列表。接下来，我们看到实际的下一个值，即 106.258606。最后，我们看到预测的下一个值 105.36248。我们得到了一个合理的预测，但我们如何衡量随着时间的推移的准确性？我们将在下一节中进行探讨。

探索整体预测

在在上一节中，您了解了如何通过基于窗口大小（在本例中为 20）获取前一组值并将它们传递给模型来获得给定时间点的预测。要查看模型的总体结果，您必须对每个时间步执行相同的操作。

你可以用这样一个简单的循环来做到这一点：

forecast = []
for time in range(len(series) - window_size):
    forecast.append(
        model.predict(series[time:time + window_size][np.newaxis]))

首先，您创建一个名为的新数组forecast，它将存储预测值。然后，对于原始系列中的每个时间步，您调用该predict方法并将结果存储在forecast数组中。您不能对数据中的前n 个元素执行此操作，其中n是window_size，因为此时您将没有足够的数据来进行预测，因为每个预测都需要n 个先前值。

当此循环完成时，forecast数组将具有时间步长 21 之后的预测值。

如果您还记得的话，您还在时间步长 1,000 处将数据集拆分为训练集和验证集。因此，对于下一步，您也应该只从此时开始进行预测。由于您的预测数据已经偏离 20（或任何您的窗口大小），您可以将其拆分并将其转换为 Numpy 数组，如下所示：

forecast = forecast[split_time-window_size:]
results = np.array(forecast)[:, 0, 0]

它现在与预测数据的形状相同，因此您可以像这样将它们相互绘制：

plt.figure(figsize=(10, 6))

plot_series(time_valid, x_valid)
plot_series(time_valid, results)

该图将类似于图 10-3。

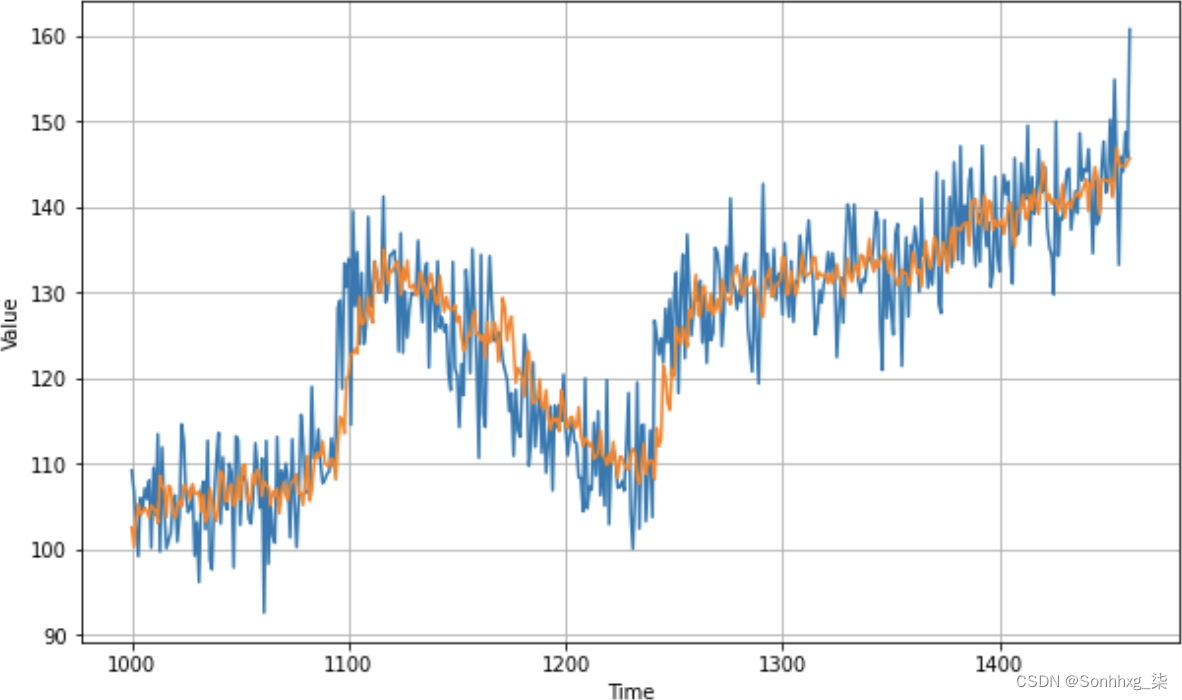
图 10-3。根据值绘制预测

通过快速目视检查，您可以看到预测不错。它通常遵循原始数据的曲线。当数据发生快速变化时，预测需要一点时间才能赶上，但总的来说还不错。

但是，在观察曲线时很难做到精确。最好有一个好的指标，在第 9 章中您已经了解了一个指标——MAE。现在您有了有效数据和结果，您可以使用以下代码测量 MAE：

tf.keras.metrics.mean_absolute_error(x_valid, results).numpy()

数据中引入了随机性，因此您的结果可能会有所不同，但当我尝试它时，我得到的 MAE 值为 4.51。

你可能会争辩说，让预测尽可能准确的过程就变成了最小化 MAE 的过程。您可以使用一些技术来执行此操作，包括明显更改窗口大小。我将留给您进行试验，但在下一节中，您将对优化器进行一些基本的超参数调整，以改进神经网络的学习方式，并查看这将对 MAE 产生什么影响。

调整学习率

在在前面的示例中，您可能还记得您使用如下所示的优化器编译模型：

model.compile(loss="mse",
              optimizer=tf.keras.optimizers.SGD(lr=1e-6, momentum=0.9))

在这种情况下，您使用的学习率为 1 × 10 –6。但这似乎是一个非常随意的数字。如果你改变它呢？你应该如何改变它？需要进行大量实验才能找到最佳比率。

为您提供的一件事tf.keras是回调，可帮助您随时间调整学习率。您在第 2 章了解了回调——在每个纪元结束时调用的函数，当精度达到了期望值。

您还可以使用回调来调整学习率参数，绘制该参数的值与适当时期的损失的关系，并从那里确定要使用的最佳学习率。

为此，只需创建一个tf.keras.callbacks.LearningRateScheduler并让它lr用所需的起始值填充参数。这是一个例子：

lr_schedule = tf.keras.callbacks.LearningRateScheduler(
    lambda epoch: 1e-8 * 10**(epoch / 20))

在这种情况下，您将从 1e–8 开始学习率，然后每个时期都将其增加少量。当它完成一百个 epoch 时，学习率将达到大约 1e–3。

现在您可以使用 1e–8 的学习率初始化优化器，并指定您要在调用中使用此回调model.fit：

optimizer = tf.keras.optimizers.SGD(lr=1e-8, momentum=0.9)
model.compile(loss="mse", optimizer=optimizer)
history = model.fit(dataset, epochs=100, 
                     callbacks=[lr_schedule], verbose=0)

正如您使用history=model.fit的那样，训练历史为您存储，包括损失。然后，您可以将其与每个时期的学习率作图，如下所示：

lrs = 1e-8 * (10 ** (np.arange(100) / 20))
plt.semilogx(lrs, history.history["loss"])
plt.axis([1e-8, 1e-3, 0, 300])

这个只需lrs使用与 lambda 函数相同的公式设置值，并将其与 1e-8 和 1e-3 之间的损失进行对比。图 10-4显示了结果。

图 10-4。绘制损失与学习率

因此，虽然之前您将学习率设置为 1e–6，但看起来 1e–5 的损失较小，因此现在您可以返回模型并使用 1e–5 重新定义它作为新的学习率。

训练模型后，您可能会注意到损失有所减少。就我而言，学习率为 1e-6 时，我的最终损失为 36.5，但学习率为 1e-5 时，它减少到 32.9。然而，当我对所有数据进行预测时，结果是图 10-5中的图表，如您所见，它看起来有点偏差。

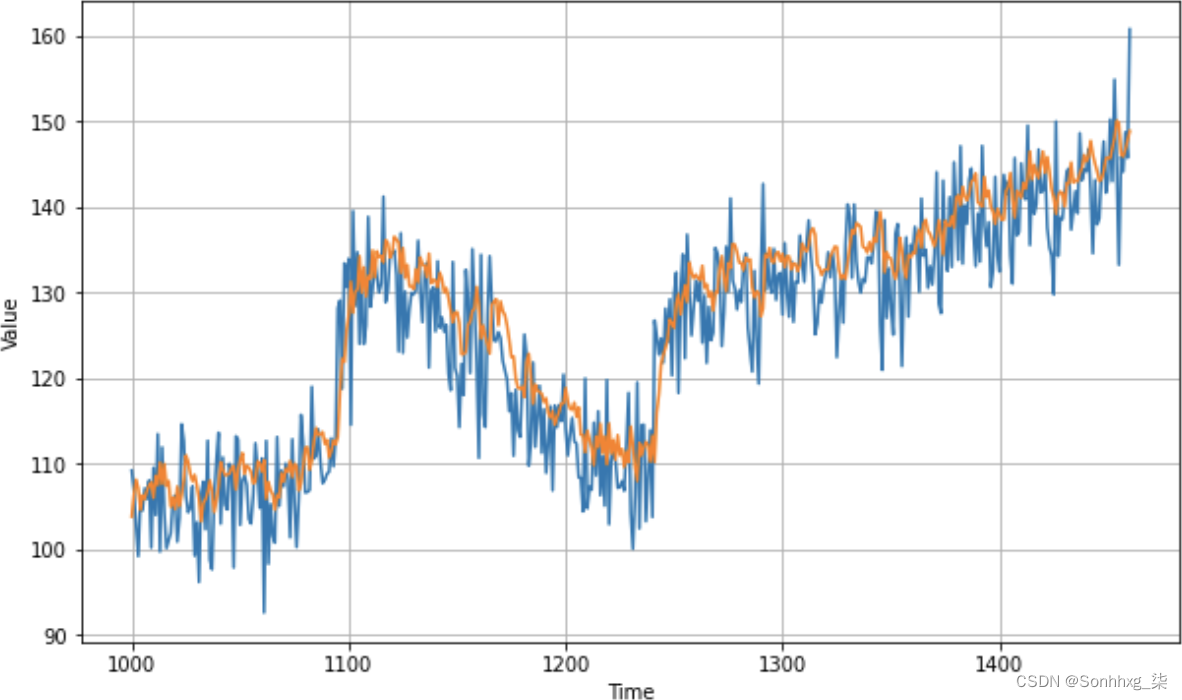
图 10-5。具有调整后学习率的图表

而当我测量 MAE 时，它最终为 4.96，所以它退步了一小步！话虽这么说，一旦知道自己拥有最佳学习率，就可以开始探索其他方法来优化网络性能。一个简单的起点是窗口的大小——20 天的数据预测 1 天可能不够，所以您可能想尝试 40 天的窗口。另外，尝试训练更多的时代。通过一些实验，您可以获得接近 4 的 MAE，这还不错。

使用 Keras Tuner 探索超参数调整

在在上一节中，您了解了如何对随机梯度下降损失函数的学习率进行粗略优化。这当然是一项非常艰巨的工作，每隔几个时期改变学习率并测量损失。它也受到损失函数已经存在的事实的影响将 epoch 更改为 epoch，因此您实际上可能没有找到最佳值，而是一个近似值。要真正找到最佳值，您必须用每个潜在值训练完整的 epoch 集，然后比较结果。这只是一个超参数，学习率。如果你想找到最好的动量，或者调整其他东西，比如模型架构——每层有多少神经元，有多少层等等——你最终可以有成千上万的选项来测试，并且对所有这些进行训练很难编码。

幸运的是，Keras Tuner 工具使这变得相对容易。pip您可以使用一个简单的命令安装 Keras Tuner ：

!pip install keras-tuner

然后，您可以使用它来参数化您的超参数，指定要测试的值范围。Keras Tuner 将训练多个模型，一个模型具有每组可能的参数，根据您想要的指标评估模型，然后报告最佳模型。我不会在这里详细介绍该工具提供的所有选项，但我将向您展示如何将它用于该特定模型。

假设我们只想试验两件事，第一件事是模型架构中输入神经元的数量。一直以来，您都有一个包含 10 个输入神经元的模型架构，然后是 10 个隐藏层，然后是输出层。但是网络可以做得更好吗？例如，如果您可以在输入层中试验多达 30 个神经元会怎么样？

回想一下输入层是这样定义的：

tf.keras.layers.Dense(10, input_shape=[window_size], activation="relu"),

如果你想测试不同于硬编码 10 的值，你可以将它设置为循环遍历多个整数，如下所示：

tf.keras.layers.Dense(units=hp.Int('units', min_value=10, max_value=30, step=2), 
                      activation='relu', input_shape=[window_size])

在这里，您定义该层将使用多个输入值进行测试，从 10 开始，以 2 为步长增加到 30。现在，Keras Tuner 将训练模型 11 次，而不是只训练一次模型并看到损失！

此外，当您编译模型时，您将momentum参数的值硬编码为0.9. 从模型定义中回忆这段代码：

optimizer = tf.keras.optimizers.SGD(lr=1e-5, momentum=0.9)

您可以将其更改为通过几个选项循环，而不是使用hp.Choice构造。这是一个例子：

optimizer=tf.keras.optimizers.SGD(hp.Choice('momentum', 
                                  values=[.9, .7, .5, .3]), 
                                  lr=1e-5)

这提供了四种可能的选择，因此，当结合之前定义的模型架构时，您将最终循环通过 44 种可能的组合。Keras Tuner 可以为您完成这项工作，并报告表现最好的模型。

要完成此设置，首先创建一个为您构建模型的函数。这是一个更新的模型定义：

def build_model(hp):
    model = tf.keras.models.Sequential()
    model.add(tf.keras.layers.Dense(
       units=hp.Int('units', min_value=10, max_value=30, step=2), 
                   activation='relu', input_shape=[window_size]))
    model.add(tf.keras.layers.Dense(10, activation='relu'))
    model.add(tf.keras.layers.Dense(1))

    model.compile(loss="mse", 
                  optimizer=tf.keras.optimizers.SGD(hp.Choice('momentum', 
                                                 values=[.9, .7, .5, .3]), 
                                                 lr=1e-5))

    return model

现在，安装 Keras Tuner 后，您可以创建一个RandomSearch对象来管理该模型的所有迭代：

tuner = RandomSearch(build_model, 
                     objective='loss', max_trials=150, 
                     executions_per_trial=3, directory='my_dir', 
                     project_name='hello')

请注意，您通过将模型传递给您之前描述的函数来定义模型。超参数参数 ( hp) 用于控制更改哪些值。您将指定objective为loss，表明您希望最小化损失。您可以使用该参数限制要运行的试验总数max_trials，并指定使用该参数训练和评估模型的次数（在某种程度上消除随机波动）executions_per_trial。

要开始搜索，您只需tuner.search像往常一样调用model.fit。这是代码：

tuner.search(dataset, epochs=100, verbose=0)

使用您在本章中一直在研究的合成系列运行它，然后将根据您对要尝试的选项的定义使用每个可能的超参数训练模型。

完成后，您可以调用tuner.results_summary它，它会根据目标为您提供前 10 项试验：

tuner.results_summary()

你应该看到这样的输出：

Results summary
|-Results in my_dir/hello
|-Showing 10 best trials
|-Objective(name='loss', direction='min')
Trial summary
|-Trial ID: dcfd832e62daf4d34b729c546120fb14
|-Score: 33.18723194615371
|-Best step: 0
Hyperparameters:
|-momentum: 0.5
|-units: 28
Trial summary
|-Trial ID: 02ca5958ac043f6be8b2e2b5479d1f09
|-Score: 33.83273440510237
|-Best step: 0
Hyperparameters:
|-momentum: 0.7
|-units: 28

从结果中可以看出，最佳损失分数是在动量为 0.5 和 28 个输入单元时获得的。您可以通过调用并指定您想要的数量来检索此模型和其他顶级模型get_best_models——例如，如果您想要前四名模型，您可以这样调用它：

tuner.get_best_models(num_models=4)

然后您可以测试这些模型。

或者，您可以使用学习到的超参数从头开始创建一个新模型，如下所示：

dataset = windowed_dataset(x_train, window_size, batch_size, 
                           shuffle_buffer_size)

model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(28, input_shape=[window_size], 
                           activation="relu"), 
    tf.keras.layers.Dense(10, activation="relu"), 
    tf.keras.layers.Dense(1)
])

optimizer = tf.keras.optimizers.SGD(lr=1e-5, momentum=0.5)
model.compile(loss="mse", optimizer=optimizer)
history = model.fit(dataset, epochs=100,  verbose=1)

当我使用这些超参数进行训练，并像之前一样对整个验证集进行预测时，我得到了一个如图 10-6 所示的图表。

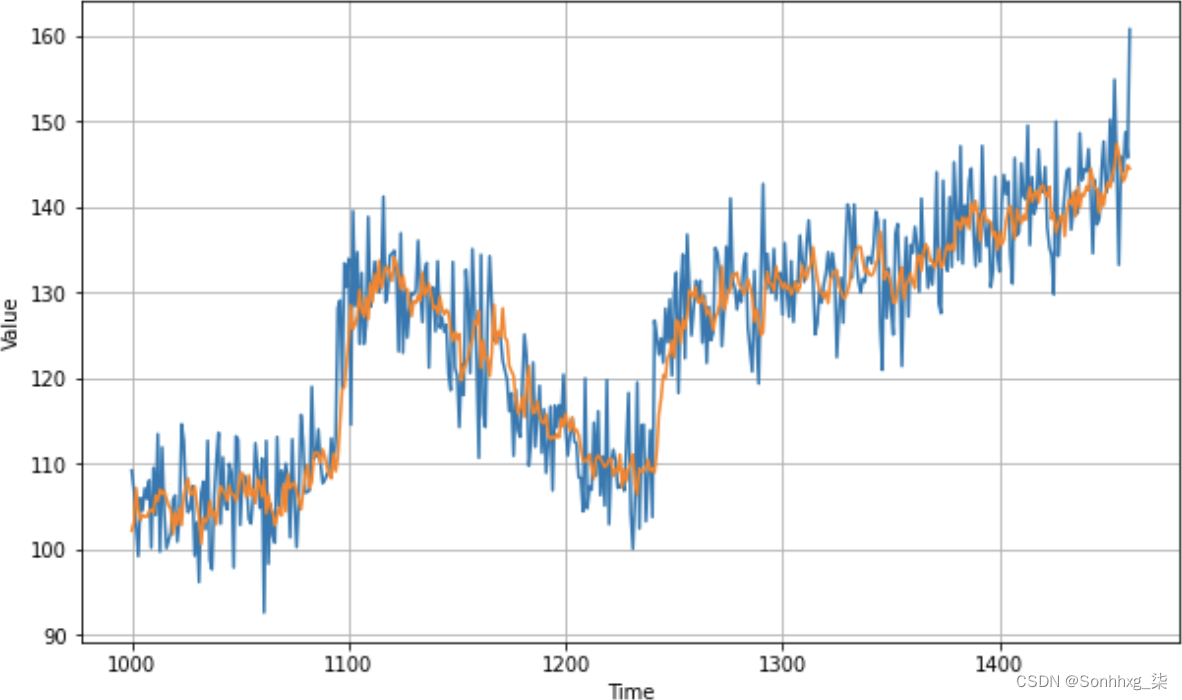
图 10-6。具有优化超参数的预测图

对此的 MAE 计算得出 4.47，这比原来的 4.51 略有改进，但比上一章的统计方法得到的结果 5.13 有了很大改进。这是在学习率更改为 1e-5 的情况下完成的，这可能不是最佳的。使用 Keras Tuner，您可以调整超参数，调整中间层的神经元数量，甚至可以试验不同的损失函数和优化器。试一试，看看你是否可以改进这个模型！

概括

在本章中，您对第 9 章中的时间序列进行了统计分析，并应用机器学习来尝试更好地进行预测。机器学习实际上就是模式匹配，正如预期的那样，您能够将平均误差降低近 10%，方法是首先使用深度神经网络来发现模式，然后使用 Keras Tuner 进行超参数调整来改进损失并提高准确率。在第 11 章中，您将超越简单的 DNN 并检查使用循环神经网络预测序列值的含义。