👨‍🎓个人主页：研学社的博客 

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

---

💥1 概述

本文讲解了如何应用Sharfetter-Gummel和改进的Sharfetter-Gummel程序来计算对流扩散方程的通量。此外，还利用了用于时间离散化的线法（MOL）和用于空间通量导数的有限体积（FV）。

文章来源：

下载链接：A More Accurate Scharfetter-Gummel Algorithm of Electron Transport for Semiconductor and Gas Discharge Simulation - ScienceDirect

改进了著名的Scharfetter-Gummmel（SG）方案，用于半导体和气体放电等离子体的对流主导问题。考虑了一维对流-扩散方程。结果表明，如果两个相邻节点之间的电位降远小于电子温度，则原始SG方案是准确的。为了满足此条件，在相邻节点之间插入了一对附加节点。这些“虚拟”节点之间的距离可以选择得足够小，以高精度获得细胞结合处的通量。虚拟节点上的数字密度是通过插值法找到的。测试表明，该方案的精度与FCT技术相当，但相比之下，它不会对快速变化的功能产生“楼梯”干扰。

📚2 运行结果

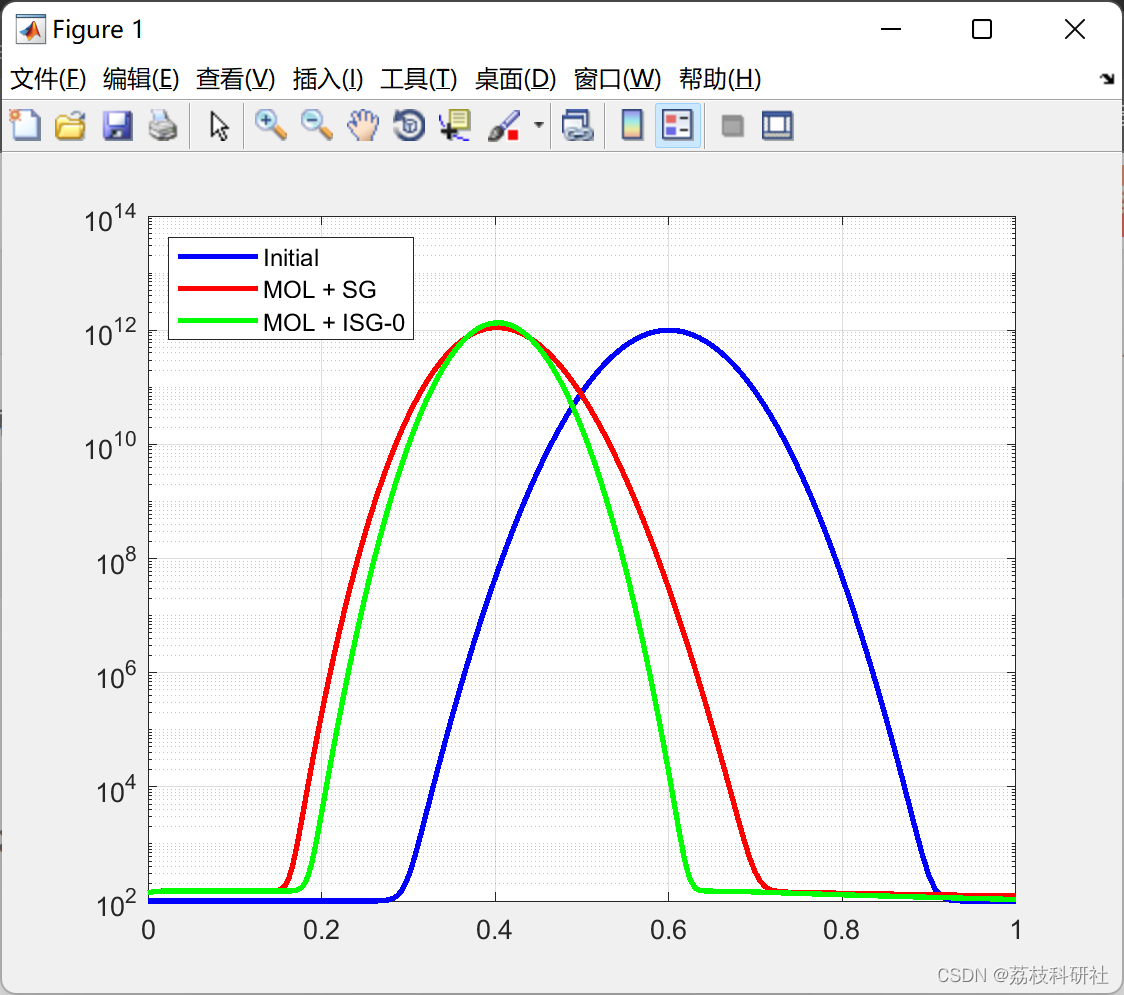
 部分代码：

%% Plot solution in dynamics
for I=1:100
    semilogy(x, u0, 'b-', x, u1(I,:), 'r-', x, u2(I,:), 'g-', 'LineWidth', 2);
    legend('Initial', 'MOL + SG', 'MOL + ISG-0', 'Location', 'NorthWest');
    xlim([0.0 1.0]);
    grid on;
    pause(0.01)
    drawnow;
end

%% MOL ODEs system with SG flux for equation 
%% convection-diffusion equation in 1D (32)
function [res] = MOL_eqs_SG(t, u)
global x
N = length(u); 
% Constants from original paper
mue = 1.0; De = 1.0; A = 1.0e+4;
% Linear field
E = A*x;

% Define spatial grid steps for non-uniform grid
h(1:N-1) = x(2:N)-x(1:(N-1)); h(N) = h(N-1); h(N+1) = h(N);

for k=1:(N-1)
    % Restrict averaged E_{k+1/2} to prevent run-time errors
    if 0.5*abs(E(k+1)+E(k))> eps
        alpha = mue*h(k)/De*0.5*(E(k+1)+E(k));
        I0 = ( exp(alpha) - 1.0 )/alpha;
        j(k+1) = De/h(k)*(u(k) - exp(alpha)*u(k+1))/I0;
    else
        j(k+1) = De/h(k)*(u(k) - u(k+1));
    end
end
% Apply simple BCs for fluxes at ghost nodes
j(1) = -A*x(1)*u(1);   j(N+1) = -A*x(N)*u(N);

% Form MOL ODEs
k = 1:N;
res(k) = -(j(k+1)-j(k))./(0.5*h(k)+0.5*h(k+1));
res = res';

%% MOL ODEs system with ISG-0 flux for equation 
%% convection-diffusion equation in 1D (32)
function [res] = MOL_eqs_ISG(t,u)
global x
N = length(u); 
% Constants from original paper
mue = 1.0; De = 1.0; A = 1.0e+4; epsilon = 0.01;
% Linear field
E = A*x;

h(1:N-1) = x(2:N)-x(1:(N-1)); h(N) = h(N-1); h(N+1) = h(N);

for k=1:(N-1)
    % Distance between virtual nodes h_v (see (21))
    h_v = sqrt(2.0*epsilon*De*h(k)/mue/abs(E(k+1)-E(k)));
    % If h_v>=h then use SG scheme
    if (h_v >= h(k))        
        if 0.5*abs(E(k+1)+E(k))> eps
            alpha = mue*h(k)/De*0.5*(E(k+1)+E(k));
            I0 = ( exp(alpha) - 1.0 )/alpha;
            j(k+1) = De/h(k)*(u(k) - exp(alpha)*u(k+1))/I0;
        else
            j(k+1) = De/h(k)*(u(k) - u(k+1));
        end
    % If h_v<h then use ISG-0 (24)-(25)   
    else
        if 0.5*abs(E(k+1)+E(k))> eps
            x_L = (x(k)+x(k+1)-h_v)/2; 
            x_R = (x(k)+x(k+1)+h_v)/2;
            alpha_v = h_v*mue/De*0.5*(E(k+1)+E(k));
            I0 = ( exp(alpha_v) - 1.0 )/alpha_v;
            j(k+1) = De/h_v*(interp1(x, u, x_L, 'pchip') - exp(alpha_v)*interp1(x, u, x_R, 'pchip'))/I0;
        else
            j(k+1) = De/h_v*(interp1(x, u, x_L, 'pchip') - interp1(x, u, x_R, 'pchip'));            
        end
    end
end
% Apply simple BCs for fluxes at ghost nodes
j(1) = -A*x(1)*u(1);   j(N+1) = -A*x(N)*u(N);

% Form MOL ODEs
k = 1:N;
res(k) = -(j(k+1)-j(k))./(0.5*h(k)+0.5*h(k+1));
res = res';

🌈3 Matlab代码实现

🎉4 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]"A More Accurate Sharfetter-Gummel Algorithm of Electron Transport for Semiconductor and Gas Discharge Simulation" // Journal of Computational Physics, 119, pp.149-155 (155).