1.常微分方程
普通边界
已知t0时刻的初值 ode45() 龙格-库塔法 一阶,高阶都一样 如下:
s(1) = y , s(2)=y'
s(3) = x , s(4)=x'
//匿名函数 下为方程组 核心函数
s_chuzhi = [0;0;0;0]; //初值 分别两个位移和速度的初值
t0 = 0:0.2:180;
f = @(t,s)[s(2);(f*cos(w*t) - K1*s(2) - s(1)*rou*g*Aw - K2*(s(1) - s(3)) - K3*(s(2)-s(4)) ) / (m+namd);
s(4);( K2*(s(1)-s(3)) + K3*(s(2)-s(4)) ) / m1];
[t,s] = ode45(f,t0,s_chuzhi);分段边界 非匿名函数
% 主函数
s_chuzhi = [0;0;0]; % 位移,速度,加速度的初值
t0 = 0:0.2:180;
[t,s] = ode45(@f1,t0,s_chuzhi);
% f1函数
% s(1) = s , s(2) =s' , s(3) = s''
function ds = (t,s)
ds = zeros(3,1); %有更高阶的可以初始化为 4,1 5,1 等等
%分段 可以是以函数值或自变量时间分段
if ...
s(1) = ... %s
s(2) = ... %s'
s(3) = ... %s'' 下同
else if ...
s(1) = ...
s(2) = ...
s(3) = ...
else ...
s(1) = ...
s(2) = ...
s(3) = ...
end


手写改进的ode45()函数代码
function varargout=odes_rk4(odefun,xspan,y0,n)
% 经典四阶 Runge-Kutta 法求解微分方程组
if nargin<4
n=10; % 默认区间等分数为 10
end
w=length(y0); % 方程的维数
x=linspace(xspan(1),xspan(2),n+1); % 离散节点值
y=[y0(:),zeros(w,n)].'; % 存储微分方程的解向量
K=zeros(4,w); % 存储节点处的导数值
for k=1:n
l=x(k+1)-x(k); % 步长
K(1,:)=feval(odefun,x(k),y(k,:)); % 求 K1 的值
K(2,:)=feval(odefun,x(k)+l/2,y(k,:)+l/2*K(1,:)); % 求 K2 的值
K(3,:)=feval(odefun,x(k)+l/2,y(k,:)+l/2*K(2,:)); % 求 K3 的值
K(4,:)=feval(odefun,x(k)+l,y(k,:)+l*K(3,:)); % 求 K4 的值
y(k+1,:)=y(k,:)+l/6*[1,2,2,1]*K; % 经典四阶 Runge-Kutta 公式
end
[varargout{1:2}]=deal(x(:),... % 第一个输出参数为离散节点值
y); % 第二个输出参数为微分方程的解复杂边界值(即已知初始值,也知道末尾值),用bvp4c()函数
2.偏微分方程
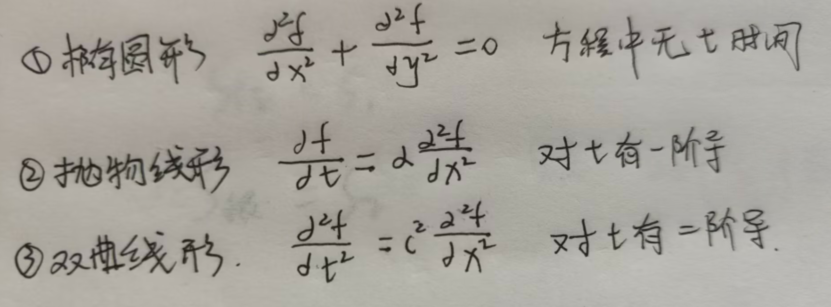
1. pdepe()函数 椭圆-抛物线型
控制方程 左边界 右边界 初始值
标准格式
初始值格式
边界值标准格式 左边界 右边界 两个方程
m = 0; % m 结合标准方程求出
x = [0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t = [0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t); %有三个函数
u1 = sol(:,:,1);
u2 = sol(:,:,2);
figure
surf(x,t,u1)
title('u1(x,t)')
xlabel('Distance x')
ylabel('Time t')
figure
surf(x,t,u2)
title('u2(x,t)')
xlabel('Distance x')
ylabel('Time t')
% --------------------------------------------------------------
function [c,f,s] = pdex4pde(x,t,u,DuDx) %函数一 结合标准方程格式(1)求程求 c,f,s
c = [1; 1];
f = [0.024; 0.17] .* DuDx;
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F];
% --------------------------------------------------------------
function u0 = pdex4ic(x); %函数二 方程初始值 即t=0时刻的值
u0 = [1; 0];
% --------------------------------------------------------------
function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t) %结合左边界标准格式(3)求p,q
pl = [0; ul(2)]; %结合右边界标准格式(3)求p,q
ql = [1; 0];
pr = [ur(1)-1; 0];
qr = [0; 1];
2.一维热传导方程解法
clc,clear;
a=1; %热传导方程中的
dx=0.02; %尽量大
x=0:dx:1;
dt=0.0001; %尽量小
t=0:dt:1;
%构造温度分布矩阵
u=zeros(length(x),length(t));
u(:,1)=sin(pi*x); %初始条件 可以改
m1=10+0.5*sin(t); %左边界条件 可以改 m1就是那个μ1 ,本子上记的
m2=10-0.5*sin(10*t); %右边界条件 可以改 m2就是那个μ2
%系数矩阵
A=-2*eye(length(x))+diag(ones(1,length(x)-1),1)+diag(ones(1,length(x)-1),-1);
for n=1:length(t)-1
u(:,n+1)=u(:,n)+(a^2*dt/dx^2)*A*u(:,n) ; %A是系数矩阵 a是热传导方程公式中的
%第一类边界条件的话
u(1,n+1)=m1(n+1); %单独计算每一行的左边界值
u(end,n+1)=m2(n+1); %单独计算每一行的右边界值
%第二类边界条件的话
%u(1,n+1)=u(2,n+1)-m1(n+1)*dx;
%u(end,n+1)=u(end-1,n+1)+m2(n+1)*dx;
%第三类边界条件的话
end
plot(x,u(:,end)); %画出最后一行
figure
[T,X]=meshgrid(t,x);
surf(X,T,u);
shading interp
%% 加热源 f
clc,clear;
a=1; %热传导方程中的
dx=0.02; %尽量大
x=0:dx:1;
dt=0.00001; %尽量小
t=0:dt:1;
%构造温度分布矩阵
u=zeros(length(x),length(t));
u(:,1)=0; %t=0初始条件 可以改
f=20*exp(-20*(x-1/2).^2); %热源
m1=0+0.0*sin(t); %左边界条件 可以改
m2=0-0.0*sin(10*t); %右边界条件 可以改
%系数矩阵
A=-2*eye(length(x))+diag(ones(1,length(x)-1),1)+diag(ones(1,length(x)-1),-1);
c=1;
for n=1:length(t)-1
u(:,n+1)=u(:,n)+(a^2/dx^2*A*u(:,n)+f')*dt ; %A是系数矩阵 a是热传导方程公式中的
%第一类边界条件的话
%u(1,n+1)=m1(n+1); %单独计算每一行的左边界值
%u(end,n+1)=m2(n+1); %单独计算每一行的右边界值
%第二类边界条件的话
%u(1,n+1)=u(2,n+1)-m1(n+1)*dx;
%u(end,n+1)=u(end-1,n+1)+m2(n+1)*dx;
%第三类边界条件的话
u(1,n+1)=(dx*m1(n+1)-c*u(2,n+1)) / (dx-c); % c为公式中的系数 具体看笔记
u(end,n+1)=(dx*m2(n+1)+c*u(end-1,n+1)) / (dx+c);
end
plot(x,u(:,end)); %画出最后一行
%axis([x(1) x(end) 0 1]);
figure
[T,X]=meshgrid(t,x);
surf(X,T,u);
shading interp3.一维波动方程 b站吴一东
3.最小二乘法
实际的一组数据和拟合出来的一组数据进行逐个:
(1)作差
(2)平方
(3)再求和
(4)再迭代使得和越来越小(迭代用随机优化算法或变步长算法遍历都行)
(5)画图 拟合图 还有的看论文
需要画神魔图?????
4.二分搜索法 适合单变量,单目标最优化算法
主要适合于单变量,单调函数
% 单变量优化
clc,clear
xmin = 1;
xmax = 5;
x = xmin:0.0001:xmax;
yy = ones(1,length(x)).*4;
plot(x,exp(x),x,yy,' r:');
i = 1;
hold on
while (abs(xmax-xmin)>1e-5)
xmid(i) = (xmax+xmin)/2; %取中点 自变量
ymid(i) = exp(xmid(i)); %将中点带入函数计算结果 因变量 前提函数得是单调函数
if ymid(i)>4 % 4为函数目标值 这是已知了函数目标值
xmax = xmid(i);
else
xmin = xmid(i);
end
plot(xmid(i),ymid(i),'ro'); %要画中点收敛图
hold on
i=i+1;
end
figure
plot(xmid,'k');
xlabel('迭代次数');
ylabel('中点位置变化');
figure
plot(ymid,'k');
xlabel('迭代次数');
ylabel('中点位置处的函数值变化');
5.遗传算法
6.绘图
1.多条线在同一张图上,不同颜色,不同线段
figure
plot(t(1,:),T(11,:),'-');
hold on
plot(t(1,:),T(21,:),'--');
plot(t(1,:),T(31,:),':');
plot(t(1,:),T(41,:)'-.');
plot(t(1,:),T(51,:));
plot(t(1,:),T(61,:));
plot(t(1,:),T(71,:));
plot(t(1,:),T(81,:));
hold off
legend({'x=0.3','x=0.6','x=3.6','x=6.6','x=8.4','x=10.2','x=12.7','x=15.2'},'Location','southeast','NumColumns',2);

2.三维图函数
mesh(),plot3(), scatter(), scatter3()
figure
[t,x] = meshgrid(t,x);
surf(t,x,T)
shading interp
3.数据导入函数xlsread()
data = xlsread('实验数据.xlsx',2); %提取表格二数据
t = data(:,1); %表格二第一列数据
T_test = data(:,2); %表格二第二列数据
7.随机优化算法(2018问题一)+ 最小二乘法或其他 --- > 数据拟合

8.梯度法-最优化算法
得画U型图 算法具有局限性
算法:
9.多起点全局搜索算法(MultiStart 算法)
10.定积分与不定积分
1.不定积分: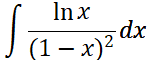
在int命令中加入积分限,就可以求得函数的定积分值。
syms x
>> int(log(x)/(1-x)^2)
ans =
- log(x/(x - 1)) - log(x)/(x - 1) %不定积分求出来为解析解
2.定积分: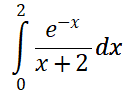
syms x
>> d = int(exp(-x)/(x+2),x,0,2)
d =
-exp(2)*(ei(-2) - ei(-4))
>> double(d)
ans =
0.333 %定积分求出来为数值解11.求解常微分,偏微分方程的通解,特解 dsolve -> 链接
12.近五年国A题
2016 系泊系统的设计
2017 CT系统参数标定及成像
2018 高温作业专用服装设计
2019 高压油管的压力控制
2020 炉温曲线
2021 “FAST”主动反射面的形状调节