寻找两个正序数组的中位数K个一组翻转链表

文章目录

- - 1. [寻找两个正序数组的中位数](https://leetcode.cn/problems/median-of-two-sorted-arrays/)
  - 2. [K个一组翻转链表](https://leetcode.cn/problems/reverse-nodes-in-k-group/)

1. 寻找两个正序数组的中位数

首先，
中位数的作用就是将正序数组的两端进行分割，假设A数组的数目是m,B数组中元素个数是n个，如果合并之后的数组数目是偶数，左右的数组个数是相同的并且满足left_max<right_min, 中位数就是 (left_max+right_min)/2 如果合并之后的数组数目是奇数，我们让左边的比右边的多一个，中位数就是左边的最大值，也就是多出来的那一个left_max。

其次，
在A组的任意位置i将数组切开，i属于[0,m],A被分为两部分[0,i-1],[i,m] 在B组的任意位置j将数组切开，j属于[0,n],B被分为两部分[0,j-1],[j,n] 这样合并之后，left_A+left_b=right_A+right_B; (当为偶数时)即i+j=m-i+n-j; (当为奇数时)即i+j-1=m-i+n-j; 所以i+j=(m+n)/2 或者 i+j=(m+n+1)/2，而这两个的值相同, 得到i和j之间的关系函数式，j=(m+n+1)/2-i;

然后，
我们知道i∈[0,m]，j∈[0,n];如果m>n，也就是A的长度更长的话，函数式中的j<0就没有意义了所以我们规定m<n，如果存在m>n，我们就将两个数组交换一下，始终保持m<n,保证我们表达式中的j始终有意义；

最后，
因为都是正序数组，所以我们只需要寻找在[0,m]中寻找i的位置保证B[j-1]<=A[i]并且A[i-1]<B[j],其中j=(m+n+1)/2， i逐渐增大,j逐渐减小，j还得大于0.所以一定存在i的最大值使得A[i-1]<=B[j]; i是最大值，那么第i+1个位置A[i]>B[j],因为B组也是正序数组B[i]>B[i-1], 所以我们直接推出B[i-1]<A[i]在满足A[i-1]<=B[j]的条件之下，所以我们最后的工作只需要找i的最大值保证A[i-1]<=B[i];即可
具体细节在代码注释中：
注意：
假设 A[i−1],B[j−1],A[i],B[j]A[i−1],B[j−1],A[i],B[j] 总是存在，对于 i=0、i=m、j=0、j=n 这样的临界条件，我们只需要规定 A[−1]=B[−1]=−∞，A[m]=B[n]=∞ 即可，这样不影响前后排序。

代码如下：

double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) 
{
	//为了保证表达式中的j>=0，约定m<n 
	if(nums1.size()>nums2.size())
		return findMedianSortedArrays( nums2, nums1);

	int m=nums1.size();
	int n=nums2.size();
	int left=0,right=m;
	int l_max=0,r_min=0;

	while(left<=right)
	{
		//采用二分查找的方式解决时间复杂度的问题log(min(m,n))
		int i=(left+right)/2;
		int j=(m+n+1)/2-i;//我们自己的表达式
		//nums[-1]=-∞ nums[m]=+∞
		int nums_i1=(i==0?INT_MIN:nums1[i-1]);
		int nums_i=(i==m?INT_MAX:nums1[i]);
		int nums_j1=(j==0?INT_MIN:nums2[j-1]);
		int nums_j=(j==n?INT_MAX:nums2[j]);
		//假定在nums1[i-1],nums2[j]处分割线
		//为的就是找到最大的i使得满足A[i-1]<=B[j]
		//那样的话，B[j-1]<=A[i]必然成立
		if(nums_i1<=nums_j)
		{
			l_max=max(nums_i1,nums_j1);
			r_min=min(nums_i,nums_j);

			left=i+1;
		}
		else
		{
			right=i-1;
		}
	} 
	return (m+n)%2==0?(l_max+r_min)/2.0:l_max;
}

2. K个一组翻转链表

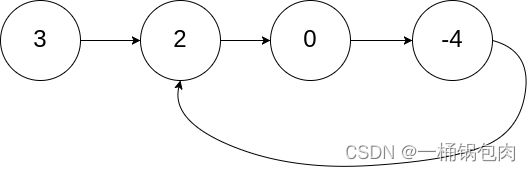
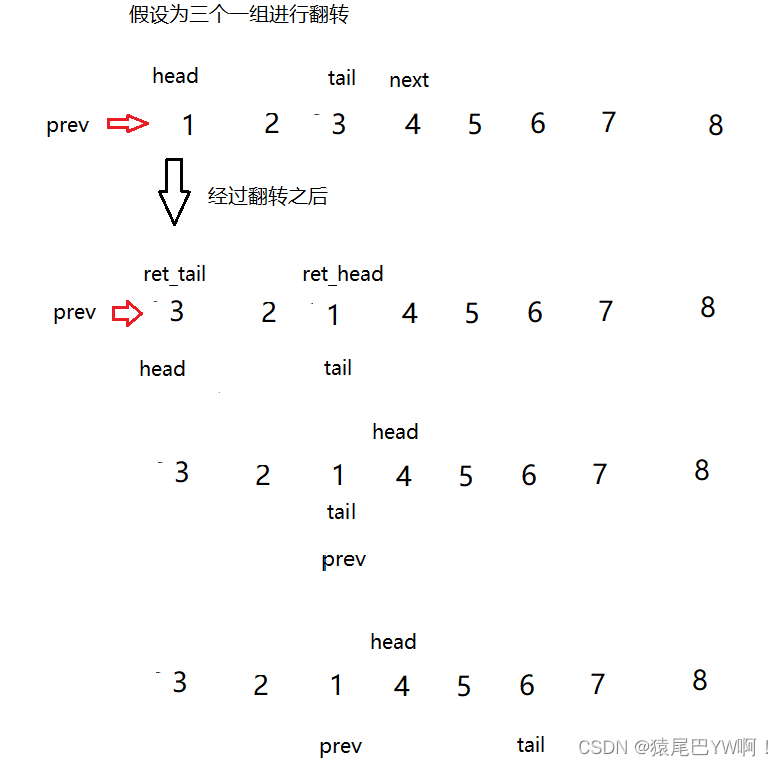
K个一组翻转链表，可以通过K找到这一组的首尾指针，然后通过子函数完成一个一组的翻转，然后返回首尾指针，接着指向下一组需要翻转的链表，主要就是首尾指针的控制和单个链表的翻转。

理解翻转一个一组的链表如下图：
理解翻转完一次之后向后找下一组中指针的变化
- 代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    pair<ListNode* ,ListNode*> reverseOneList(ListNode* head,ListNode* tail)
    {
       ListNode* prev=tail->next;
       ListNode* p=head;
       while(tail!=prev)
       {
            ListNode* next=p->next;
            p->next=prev;
            prev=p;
            p=next;
       }
       return {tail,head};
    }
    
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* hair=new ListNode(0);
        hair->next=head;
        ListNode* prev=hair;
        while(head)
        {
            ListNode* tail=prev;
            for(int i=0;i<k;i++)
            {
                tail=tail->next;
                if(!tail)
                {
                    return hair->next;
                }
            }

            ListNode* next=tail->next;
            pair<ListNode* ,ListNode*> result=reverseOneList(head,tail);
            head=result.first;
            tail=result.second;
						//重新确立连接关系
            prev->next=head;
            tail->next=next;
            //指针向后移动进行下一组的指针寻址
            prev=tail;
            head=tail->next;
        }
        return hair->next;
    }
};