🎉欢迎来到数据结构学习专栏~复杂性分析与算法设计：解锁计算机科学的奥秘

---

• ☆* o(≧▽≦)o *☆嗨~我是IT·陈寒🍹
• ✨博客主页：IT·陈寒的博客
• 🎈该系列文章专栏：数据结构学习
• 📜其他专栏：Java学习路线 Java面试技巧 Java实战项目 AIGC人工智能 数据结构学习
• 🍹文章作者技术和水平有限，如果文中出现错误，希望大家能指正🙏
• 📜 欢迎大家关注！ ❤️

---

计算机科学中的算法设计和复杂性分析是深奥而有趣的主题。它们不仅是解决计算问题的关键工具，还是评估解决方案的效率和性能的手段。在本文中，我们将深入探讨算法复杂性分析的基本概念和一些常见的算法设计策略，包括分治法、贪心法和动态规划。

算法复杂性分析的基本概念

在深入研究算法设计策略之前，让我们首先了解一些关于算法复杂性分析的基本概念。这些概念帮助我们衡量算法在不同问题规模下的性能。

时间复杂度

时间复杂度是衡量算法执行时间随输入规模增加而增加的程度。通常用大O符号（O）来表示时间复杂度。常见的时间复杂度包括：

• O(1)：常数时间，表示算法的执行时间与输入规模无关。
• O(log n)：对数时间，通常出现在分治法中，如二分查找。
• O(n)：线性时间，算法的执行时间与输入规模成正比。
• O(n log n)：线性对数时间，通常出现在快速排序和归并排序等排序算法中。
• O(n^2)：平方时间，通常出现在嵌套循环的算法中，如选择排序。
• O(2^n)：指数时间，通常出现在穷举搜索等指数级算法中。
  

空间复杂度

空间复杂度是衡量算法在执行过程中所需的内存空间量。与时间复杂度类似，通常用大O符号来表示。空间复杂度的分析有助于确定算法是否需要大量的内存，以及是否适合在内存受限的环境中运行。

常见的算法设计策略

有许多不同的算法设计策略，每种策略都适用于不同类型的问题。以下是一些常见的算法设计策略：

1. 分治法

分治法是一种将问题分解为子问题然后递归解决的策略。经典的例子包括归并排序和快速排序。这些算法将大问题分解为较小的子问题，然后将子问题的解合并在一起以获得原始问题的解。

# 示例：归并排序算法
def merge_sort(arr):
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    left_half = arr[:mid]
    right_half = arr[mid:]

    left_half = merge_sort(left_half)
    right_half = merge_sort(right_half)

    return merge(left_half, right_half)

2. 贪心法

贪心法是一种每次都选择局部最优解的策略，希望最终能够获得全局最优解。它通常用于优化问题，如最小生成树算法和Dijkstra算法。

// 示例：Dijkstra算法寻找最短路径
public int[] dijkstra(int[][] graph, int start) {
    int[] distance = new int[graph.length];
    Arrays.fill(distance, Integer.MAX_VALUE);
    distance[start] = 0;

    PriorityQueue<Integer> queue = new PriorityQueue<>();
    queue.add(start);

    while (!queue.isEmpty()) {
        int node = queue.poll();
        for (int neighbor = 0; neighbor < graph.length; neighbor++) {
            int newDist = distance[node] + graph[node][neighbor];
            if (newDist < distance[neighbor]) {
                distance[neighbor] = newDist;
                queue.add(neighbor);
            }
        }
    }

    return distance;
}

3. 动态规划

动态规划是一种将问题分解为子问题然后存储子问题的解以避免重复计算的策略。它通常用于解决具有重叠子问题性质的问题，如斐波那契数列和背包问题。

// 示例：斐波那契数列的动态规划解法
function fibonacci(n) {
    const dp = new Array(n + 1).fill(0);
    dp[1] = 1;

    for (let i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
}

算法设计的实际应用

算法设计策略不仅是计算机科学理论的一部分，还在实际问题的解决中发挥着关键作用。以下是一些实际应用示例：

1. 网络路由

在计算机网络中，路由器使用算法来确定数据包的最佳路径，以便在网络中传输。Dijkstra算法和Bellman-Ford算法是常用于路由的算法。

2. 图像处理

图像处理应用程序使用各种算法来执行任务，如图像压缩、边缘检测和物体识别。这些算法包括卷积神经网络（CNN）等。

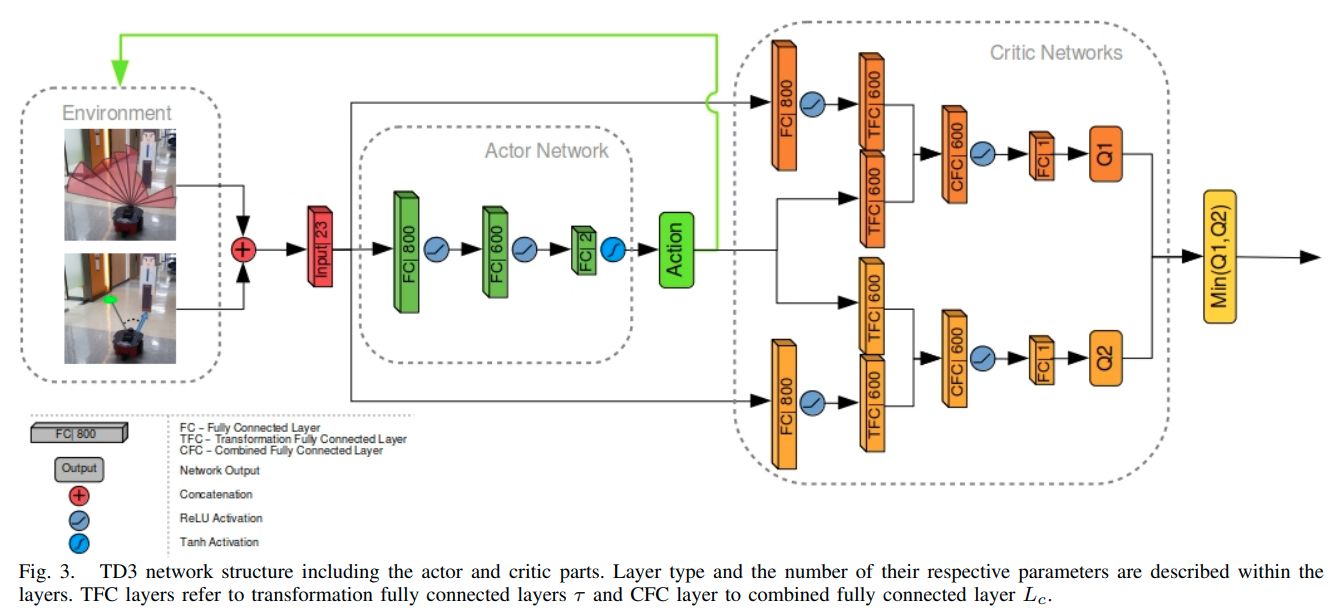
3. 人工智能

人工智能领域使用了许多复杂的算法，如深度学习中的神经网络、遗传算法和强化学习算法。这些算法用于语音识别、图像识别、自然语言处理等应用。

算法的选择和性能分析

在实际应用中，选择正确的算法至关重要。不同的算法可能在不同的情况下表现出色。因此，性能分析是一项重要的任务，可以帮助我们选择最适合特定问题的算法。

性能分析通常涉及对算法的时间复杂度和空间复杂度进行估算。时间复杂度告诉我们算法的运行时间如何随输入规模的增加而增加，而空间复杂度告诉我们算法需要多少内存。

此外，还应考虑问题的特定要求。例如，某些问题可能对算法的实时性有严格要求，而另一些问题可能更关心节省内存。因此，性能分析应综合考虑多个因素。

结论

算法设计和复杂性分析是计算机科学中的核心主题，涵盖了广泛的应用领域。无论您是计算机科学专业的学生还是从业人员，掌握这些基本概念和策略都将有助于您更好地理解和解决计算问题。深入研究不同的算法设计策略，并学会根据问题的性质选择合适的算法，将使您在计算机科学领域更上一层楼。希望本文能够帮助您在算法设计和复杂性分析方面迈出坚实的第一步。

---

🧸结尾

---

❤️ 感谢您的支持和鼓励！ 😊🙏
📜您可能感兴趣的内容：

• 【Java面试技巧】Java面试八股文 - 掌握面试必备知识（目录篇）
• 【Java学习路线】2023年完整版Java学习路线图
• 【AIGC人工智能】Chat GPT是什么，初学者怎么使用Chat GPT，需要注意些什么
• 【Java实战项目】SpringBoot+SSM实战：打造高效便捷的企业级Java外卖订购系统
• 【数据结构学习】从零起步：学习数据结构的完整路径