参考教程：
https://arxiv.org/pdf/1603.07285.pdf

---

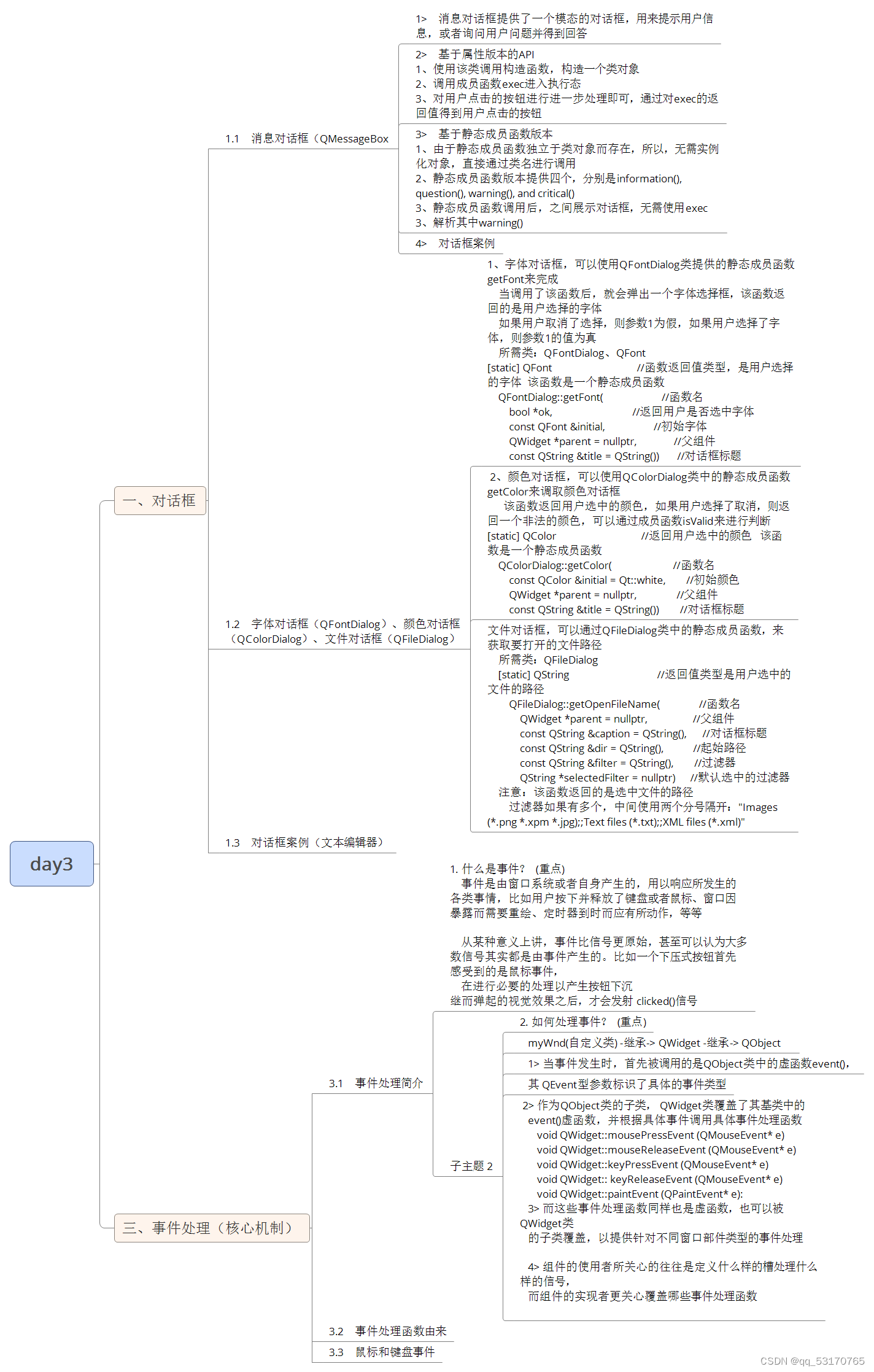
什么是转置卷积

在上一章我们说过，卷积有三种模式：full，valid，same。在full模式下，输出的特征图会比输入的特征图要大；valid模式下，输出的特征图会比输入的特征图要小；same模式下，输出的特征图会和输入的特征图大小保持一致。

full情况是很少见的，它要求卷积核的大小$k$比输入的特征图大，通过使用大小为$k-1$的padding扩充输入特征图，从而使得卷积的输出特征图大小变大。

在通常情况下，我们使用的都是valid或者same模式的卷积，并且搭配上stride=1或者stride=2，这就使得在卷积网络中逐层深入时，我们的特征图大小要么不变，要么折半，倾向于往越来越小的方向变化。

这就使得在某些要求特征图逐层变大的任务中，传统卷积就不是那么适用了。比如说语义分割任务，输出是像素级别的分割结果；或者超分辨率任务，输出图像大小至少为输入的两倍。我们当然可以用padding的方式把特征图变大，但是实际使用中效果并不好。

1. 先padding再卷积。这个其实就是转置卷积在做的事情。
2. 先卷积再padding。毫无疑问这种补全的结果对我们的任务来说是没有用的。

在这种情况下，就需要转置卷积的帮助。

转置卷积也是一种卷积操作，它实现的是我们常用的卷积的“反方向”的运算，即把一个卷积操作的输出结果还原回输入的形状，通常卷积实现的是下采样操作，转置卷积则是一种上采样方法。要注意的是这里只考虑“形状”。

如下图，输入是一个大小为4x4的特征图，使用大小为3x3的kernel进行卷积，得到大小为2x2的输出。它的转置过程，是用大小2x2的特征图做输入，得到大小4x4的输出，从结果上看，它类似于使用一个3x3的kernel在padding=(2,2,2,2)的2x2特征图上做卷积。

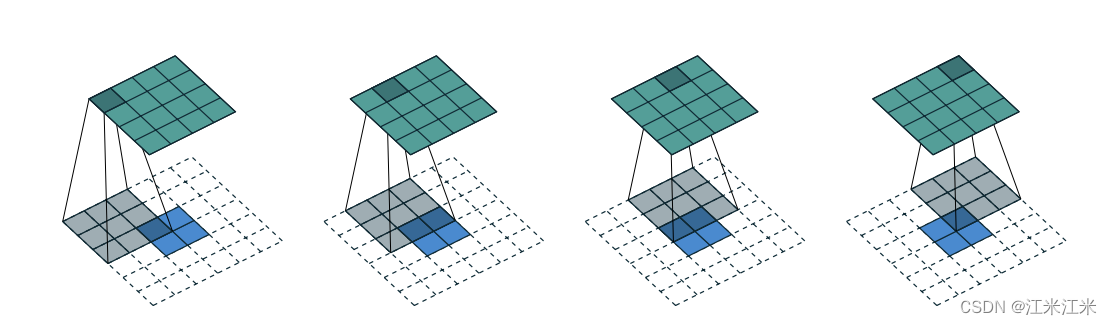
转置卷积有时候又称为反卷积，但是它本质上和反卷积还是有不同的。一方面在数学含义上反卷积是可以还原输入的值的，而转置卷积只还原形状；另一方面在深度学习中我们使用的转置卷积中的参数都是可学习的，非固定的，它的输出结果也是面向任务需求的。

转置卷积的思想

卷积操作可以形式化为一个矩阵乘法运算。

一维形式的理解

如下图，假设输入向量$x=[a,b,c,d,e,f,g{]}^T$，卷积核为$K=[x,y,z]$，卷积的滑动步长为2。

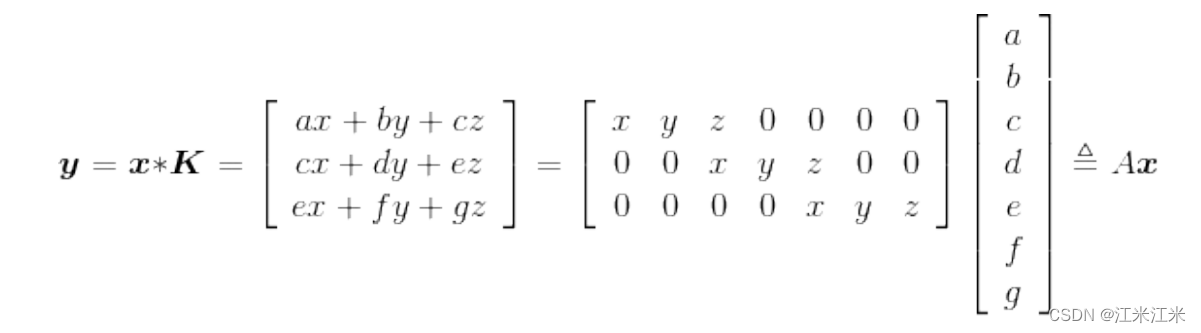
直观来看，大小为3x7的卷积矩阵A和大小为7x1的输入向量x相乘，得到大小为3x1的输出向量y。即
$$y=Ax$$
转置卷积则是将上式中的输入输出互换：
$$x=A^{T}y$$
即使用大小为7x3的转置卷积矩阵$A^T$和大小为3x1的输出向量y相乘，得到大小为7x1的输入向量x。
这样的计算只还原了输入输出的大小，但是其中的数值已经发生了变化，所以只是在形状上保持一致。

二维形式的理解

参考了https://zhuanlan.zhihu.com/p/115070523?from_voters_page=true里的例子。

对于一个输入大小为3x3的输入和大小为2x2的卷积核。
$$\begin{array}{rl}& X=\left[\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& x_{22}& x_{23}\\ x_{31}& x_{32}& x_{33}\end{array}\right]\\ & W=\left[\begin{array}{cc}{w}_{11}& w_{12}\\ w_{21}& w_{22}\end{array}\right]\end{array}$$
我们用类似于一维形式的方法，也把卷积核表示成相应的稀疏矩阵C：
$$C=\left[\begin{array}{ccccccccc}{w}_{11}& w_{12}& 0& w_{21}& w_{22}& 0& 0& 0& 0\\ 0& w_{11}& w_{12}& 0& w_{21}& w_{22}& 0& 0& 0\\ 0& 0& 0& w_{11}& w_{12}& 0& w_{21}& w_{22}& 0\\ 0& 0& 0& 0& w_{11}& w_{12}& 0& w_{21}& w_{22}\end{array}\right]$$
同时输入向量也进行展开变为：
$$x=\left[\begin{array}{ccccccccc}{x}_{11}& x_{12}& x_{13}& x_{21}& x_{22}& x_{23}& x_{31}& x_{32}& x_{33}\end{array}\right]$$
直观来看，大小为4x9的卷积矩阵C和大小为9x1的输入向量x相乘，得到大小为4x1的输出向量y。即
$$y=Cx$$
转置卷积则是将上式中的输入输出互换：
$$x=C^{T}y$$
即使用大小为9x4的转置卷积矩阵$C^T$和大小为4x1的输出向量y相乘，得到大小为9x1的输入向量x。
这样的计算只还原了输入输出的大小，但是其中的数值已经发生了变化，所以只是在形状上保持一致。

卷积和转置的关系

去理解转置卷积在给定输入特征图 $x$ 上的运算结果，我们可以去想象这个输入特征图本身是某个正向的卷积在某特定特征图上$x^{\prime }$的结果，转置卷积就是为了复原这个特定特征图$x^{\prime }$的形状。

重温一下特征图大小计算公式：
$$D_{output}=\frac{D_{input}-D_{kernel}+2\times Padding}{Stride}+1$$
先放一个别的地方偷来的计算总结，后面再详细计算：

---

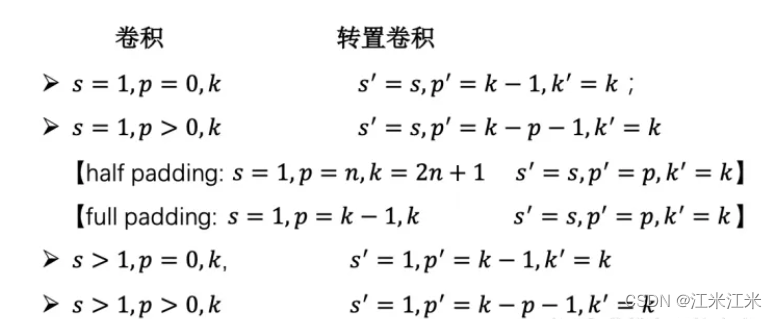
no pading, unit strides

假如$x^{\prime }$是4x4大小的特征图，我们的标准卷积操作是使用一个大小3x3的卷积核，padding=0，stride=1，得到的结果$x$是一个大小为2x2的特征图。
现在我们的转置卷积要求将$x$复原为$x^{\prime }$，我们在通过调整padding来实现这样的结果。
仍然使用大小为3x3的卷积核，stride=1，那么按照公式：
$$4=\frac{2-3+2\times Padding}{1}+1$$
代入后可以得到padding = 2。
更general的，我们列一个公式来算padding。
$$\begin{array}{rl}& D_{output}=\frac{D_{input}-D_{kernel}+2\times Padding}{Stride}+1\\ & D_{input}=\frac{D_{output}-D_{kernel}+2\times Paddin{g}^{\prime }}{Stride}+1\end{array}$$
将式子4代入3中，在stride=1的情况下，可以得到
$$Padding+1-D_{kernel}+Paddin{g}^{\prime }=0$$
在padding=0的情况下，可得到：
$$Paddin{g}^{\prime }=D_{kernel}-1$$
再将这个结果代入式子4，可以得到：
$$D_{input}=D_{output}-D_{kernel}+2\times (D_{kernel}-1)+1=D_{output}+D_{kernel}-1$$

---

padding, unit strides

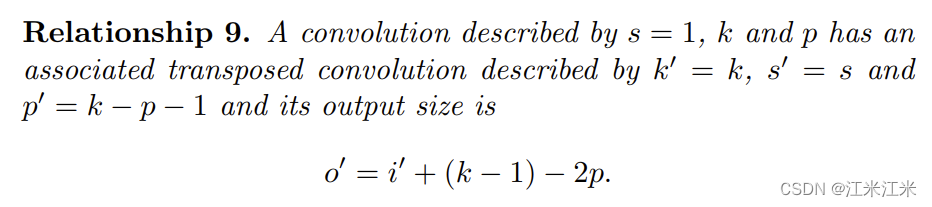
类似于no padding的情况，使用和上一节类似的公式，可以得到：
$$Paddin{g}^{\prime }=D_{kernel}-1-Padding$$
同样代入式子4，可以得到：
$$\begin{array}{rl}{D}_{input}& =D_{output}-D_{kernel}+2\times (D_{kernel}-1-Padding)+1\\ & =D_{output}+D_{kernel}-1-2\times Padding\end{array}$$

---

no padding, non-unit stride

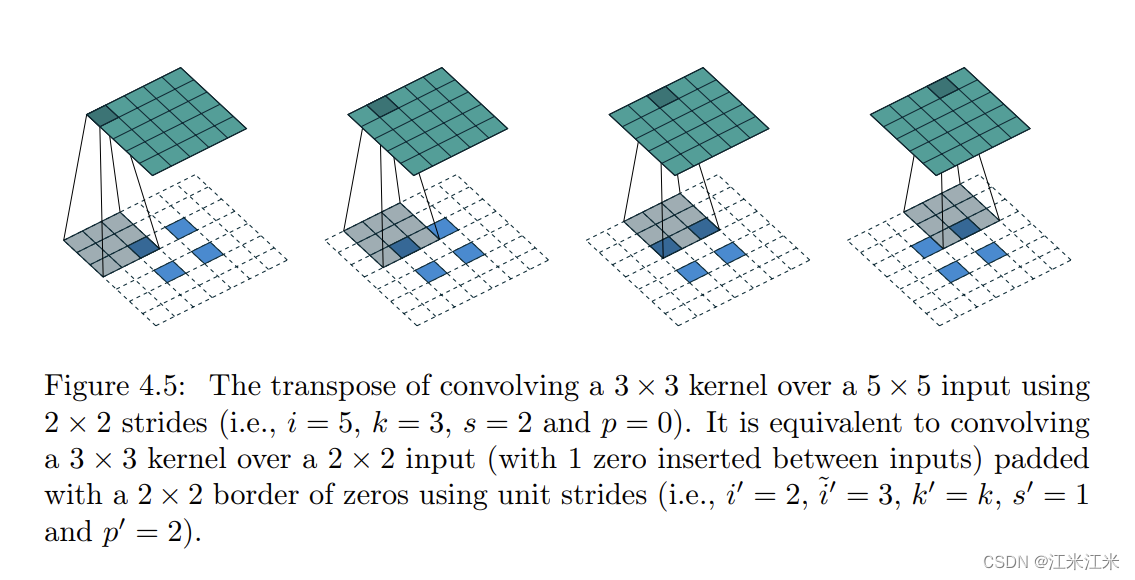
上图表示一个stride!=1的情况，假如$x^{\prime }$是5x5大小的特征图，我们的标准卷积操作是使用一个大小3x3的卷积核，padding=0，stride=2，得到的结果$x$是一个大小为2x2的特征图。
现在我们的转置卷积要求将$x$复原为$x^{\prime }$。需要再$x$的元素之间进行填充，再进行卷积。

和之前的no padding的情况一样，我们的kernel大小仍使用3x3，padding使用前面两节得到的计算结果padding = k-1，那么我们来计算一下在填充后的图像上使用的新的stride是多少。

对于当前的问题，$x^{\prime }$大小为5x5，$x$大小为2x2，在$x$的元素间填充stride-1 = 2-1 = 1个0，使它变成大小为3x3的$new\_x$。kernel大小为3x3，padding大小为2。

$$5=\frac{3-3+2\times 2}{Stride}+1$$
求得stride = 1。

更general的，我们列一个公式来算stride。
$$\begin{array}{rl}& D_{output}=\frac{D_{input}-D_{kernel}+2\times Padding}{Stride}+1\\ & D_{outpu{t}^{\prime }}=D_{output}+(Stride-1)\ast (D_{output}-1)\\ & D_{input}=\frac{D_{outpu{t}^{\prime }}-D_{kernel}+2\times Paddin{g}^{\prime }}{Stride}+1\\ & Paddin{g}^{\prime }=D_{kernel}-1\end{array}$$
公式联立后可得到：
$$Stride\times D_{output}-Stride+D_{kernel}-1=Stride\times (Stride\times D_{output}-Stride+D_{kernel}-1-2\times Padding)$$
在Padding=0的情况下，可得 $Stride=1$。

---

padding，non-unit stride

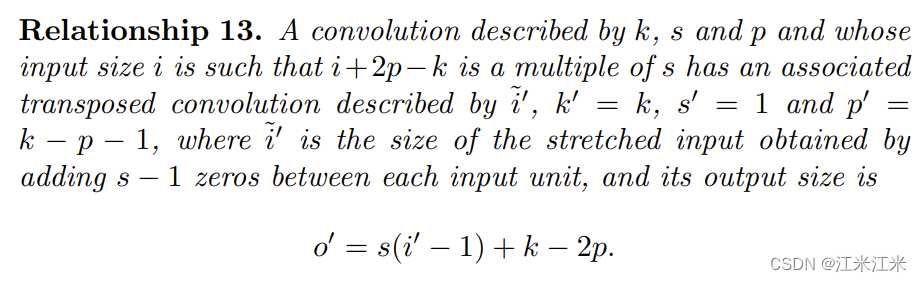
在padding不等于0的情况下，使用之前得到的公式。
$$Paddin{g}^{\prime }=D_{kernel}-1-Padding$$
用这个式子和公式7、8、9联立，可以得到。
$$Stride\times D_{output}-Stride+D_{kernel}-1-2\times Padding=Stride\times (Stride\times D_{output}-Stride+D_{kernel}-1-2\times Padding)$$
可得$Stride=1$。

pytorch中的转置卷积

根据上面的卷积和转置卷积的关系，我们来理一下它的具体实现。

转置卷积本质上就是对一个输入数据进行补零/上采样的普通卷积操作。
在有无padding，有无stride的多种情况下，kernel的大小是保持不变的。

• 对于padding：
  1. 卷积中padding=0，转置卷积的padding’=k-1。
  2. 卷积中padding不为0，转置卷积的padding‘=k-padding-1。
     归纳为 padding’ = k-padding-1
• 对于stride：
  1. 卷积中stride=1，转置卷积的stride=1，特征图不需要补0。
  2. 卷积中stride>1，转置卷积的stride=1，特征图元素间需要按stride-1的个数补0。
     归纳为，stride永远=1，但是特征图需要按stride-1进行补0。

对于一个大小为k，步长为s，padding为p的普通卷积，求它对应的转置卷积可以按如下步骤：

1. 在特征图相邻数据间进行填充，在水平和垂直方向上元素间填充s-1个0。
2. 在特征图边界进行填充，在四个边界分为进行大小为填充k-p-1的填充。
3. 在得到的特征图上进行大小为k，步长为1的普通卷积操作。

看一下pytorch中的转置卷积的实现。

https://pytorch.org/docs/stable/generated/torch.nn.ConvTranspose2d.html#torch.nn.ConvTranspose2d

CLASS torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros', device=None, dtype=None)

转置卷积和普通的卷积都继承了pytorch中的类_ConvNd，它们的初始化也没有什么区别，传参的参数名也大同小异。

我们在看介绍的时候可以看到，输入和输出的shape之间的关系是这样的。

从这个图可以看出来，实际上的操作是，output在使用当前卷积核运算处理后，得到input。这里的padding和stride都是针对output->input这一过程的。
但是在实际中我们做的是input->output这个过程，所以我们用的padding和stride都和给定的参数并不一致。

可以理解成，我们模拟了一个预想的输出使用卷积变成现在的输入的过程，然后用这个卷积的配置作为我们转置卷积的输入参数，基于此设计一个转置卷积。

使用了一个别人给的例子：

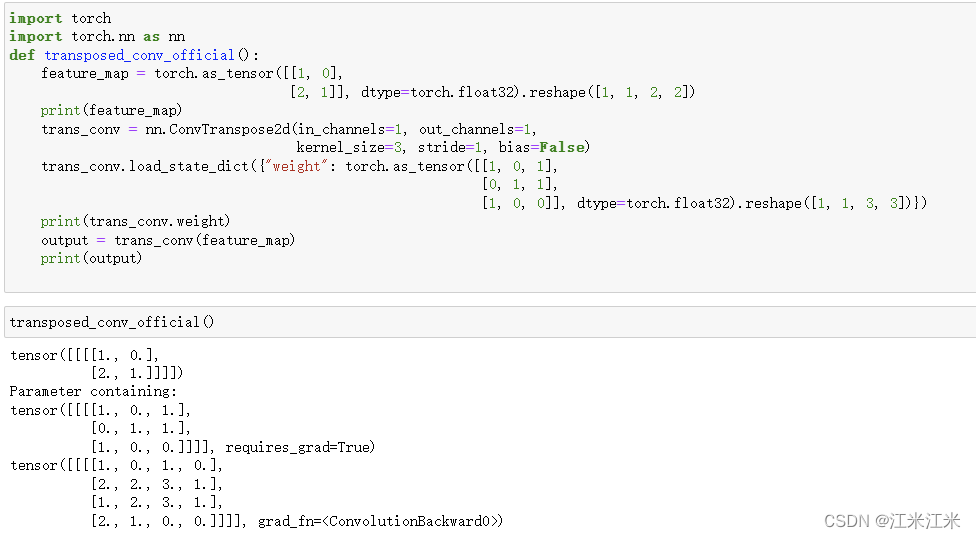
在这个例子中，我们的输入特征图大小是2x2，传入转置卷积的参数中，kernel_size=3,stride=1,padding=0。输出的特征图大小是4x4。

也就是我们用4x4的特征图做输入，使用kernel_size=3, stride=1, padding=0的卷积核，可以得到大小为2x2的输出特征图。

按照之前章节的公式理解，我们的转置卷积实际上做的操作是：

1. 给2x2特征图的元素间填充stride-1 = 1-1 = 0个0。得到2x2大小的特征图。
2. 给2x2的特征图进行大小为kernel_size-p-1 = 3-0-1-2的padding。得到大小为6x6的特征图。
3. 在6x6的特征图上使用大小为3x3的卷积核，进行步长=1的卷积运算，得到大小为4x4的输出。