🔥 本文由 程序喵正在路上 原创,CSDN首发!
💖 系列专栏:数据结构与算法
🌠 首发时间:2022年11月16日
🦋 欢迎关注🖱点赞👍收藏🌟留言🐾
🌟 一以贯之的努力 不得懈怠的人生
阅读指南
- 基本操作
- 广度优先遍历(BFS)
- 与树的广度优先遍历之间的联系
- 算法实现
- 复杂度分析
- 广度优先生成树
- 深度优先遍历(DFS)
- 与树的深度优先遍历之间的联系
- 算法实现
- 复杂度分析
- 深度优先遍历序列
- 深度优先生成树
- 图的遍历和图的连通性
基本操作
- A d j a c e n t ( G , x , y ) Adjacent(G, x, y) Adjacent(G,x,y):判断图 G G G 是否存在边 < x , y > <x, y> <x,y> 或 ( x , y ) (x, y) (x,y)
- N e i g h b o r s ( G , x ) Neighbors(G, x) Neighbors(G,x):列出图 G G G 中与结点 x x x 邻接的边
- I n s e r t V e r t e x ( G , x ) InsertVertex(G, x) InsertVertex(G,x):在图 G G G 中插入顶点 x x x
- D e l e t e V e r t e x ( G , x ) DeleteVertex(G, x) DeleteVertex(G,x):在图 G G G 中删除顶点 x x x
- A d d E d g e ( G , x , y ) AddEdge(G, x, y) AddEdge(G,x,y):若无向边 ( x , y ) (x, y) (x,y) 或有向边 < x , y > <x, y> <x,y> 不存在,则向图 G G G 中添加该边
- R e m o v e E d g e ( G , x , y ) RemoveEdge(G, x, y) RemoveEdge(G,x,y):若无向边 ( x , y ) (x, y) (x,y) 或有向边 < x , y > <x, y> <x,y> 存在,则从图 G G G 中删除该边
- F i r s t N e i g h b o r ( G , x ) FirstNeighbor(G, x) FirstNeighbor(G,x):求图 G G G 中顶点 x x x 的第一个邻接点,若有则返回顶点号;若 x x x 没有邻接点或图中不存在 x x x,则返回 − 1 -1 −1
- N e x t N e i g h b o r ( G , x , y ) NextNeighbor(G, x, y) NextNeighbor(G,x,y):假设图 G G G 中顶点 y y y 是顶点 x x x 的一个邻接点,返回除了 y y y 之外顶点 x x x 的下一个邻接点的顶点号,若 y y y 是 x x x 的最后一个邻接点,则返回 − 1 -1 −1
- G e t e d g e v a l u e ( G , x , y ) Get_edge_value(G, x, y) Getedgevalue(G,x,y):获取图 G G G 中边 ( x , y ) (x, y) (x,y) 或 < x , y > <x, y> <x,y> 对应的权值
- S e t e d g e v a l u e ( G , x , y , v ) Set_edge_value(G, x, y, v) Setedgevalue(G,x,y,v):设置图 G G G 中边 ( x , y ) (x, y) (x,y) 或 < x , y > <x, y> <x,y> 对应的权值为 v v v
广度优先遍历(BFS)
与树的广度优先遍历之间的联系
树的广度优先遍历,也就是树的层次遍历,有以下步骤:
- 若树非空,则根节点入队
- 若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队
- 重复第 2 2 2 步指导队列为空
对于树,由于树不存在 “回路”,因此在搜索相邻的结点时,不可能搜索到已经访问过的结点;而图则反之,所以我们需要对图中的结点进行标记,以此来识别这个结点是否访问过
广度优先遍历( B r e a d t h − F i r s t − S e a r c h , B F S Breadth-First-Search, BFS Breadth−First−Search,BFS)要点:
- 找到与一个顶点相邻的所有顶点
- 标记哪些顶点被访问过
- 需要一个辅助队列
在广度优先遍历中,我们需要用到两个基本操作:
- F i r s t N e i g h b o r ( G , x ) FirstNeighbor(G, x) FirstNeighbor(G,x):求图 G G G 中顶点 x x x 的第一个邻接点,若有则返回顶点号;若 x x x 没有邻接点或图中不存在 x x x,则返回 − 1 -1 −1
- N e x t N e i g h b o r ( G , x , y ) NextNeighbor(G, x, y) NextNeighbor(G,x,y):假设图 G G G 中顶点 y y y 是顶点 x x x 的一个邻接点,返回除了 y y y 之外顶点 x x x 的下一个邻接点的顶点号,若 y y y 是 x x x 的最后一个邻接点,则返回 − 1 -1 −1
算法实现
bool visited[MAX_VERTEX_NUM]; //访问标记数组,初始值都为false
void BFSTraverse(Graph G) { //对图G进行广度优先遍历
for (i = 0; i < G.vexnum; ++i) {
visited[i] = false; //访问标记数组初始化
}
InitQueue(Q); //初始化辅助队列Q
for (i = 0; i < G.vexnum; ++i) { //从0号顶点开始遍历
if (!visited[i]) //对每个连通分量调用一次BFS
BFS(G, i); //vi未访问过,从vi开始BFS
}
}
//广度优先遍历
void BFS(Graph G, int v) { //从顶点v出发,广度优先遍历图
visit(v); //访问初始顶点v
visited[v] = true; //对v做已访问标记
Enqueue(Q, v); //顶点v入队列Q
while (!isEmpty(Q)) {
DeQueue(Q, v); //顶点v出队
for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
//检测v所有邻接点
if (!visited[w]) { //w为v的未访问过的邻接顶点
visit(w); //访问顶点w
visited[w] = true; //对w做已访问标记
Enqueue(Q, w); //顶点w入队列Q
}//if
}//for
}//while
}
结论:对于无向图,调用 B F S BFS BFS 函数的次数 = = = 连通分量数(连通分量:一个极大连通子图为一个连通分量)
复杂度分析
空间复杂度:
- 最坏情况,我们访问第一个顶点时,所有顶点都和它连通,此时辅助队列大小为 O ( ∣ V ∣ ) O(|V|) O(∣V∣)
如果我们是用邻接矩阵存储的图:
- 访问 ∣ V ∣ |V| ∣V∣ 个顶点需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间
- 查找每个顶点的邻接点都需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间,而总共有 ∣ V ∣ |V| ∣V∣ 个顶点
- 时间复杂度 = O ( ∣ V ∣ 2 ) = O(|V|^2) =O(∣V∣2)
如果我们是用邻接表存储的图:
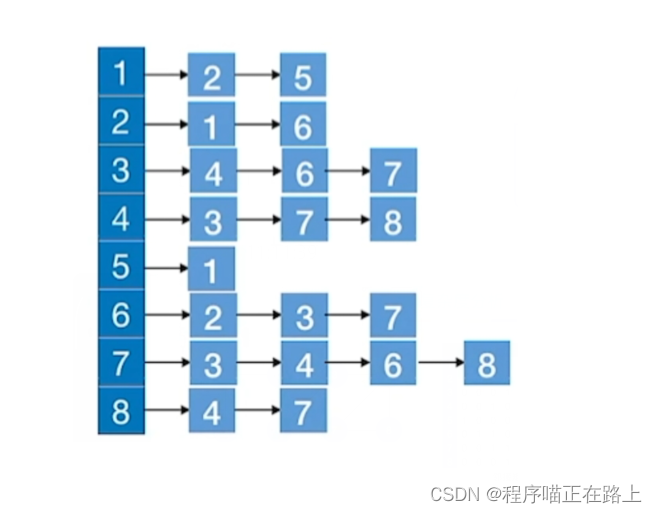
- 访问 ∣ V ∣ |V| ∣V∣ 个顶点需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间
- 查找每个顶点的邻接点共需要 O ( ∣ E ∣ ) O(|E|) O(∣E∣) 的时间
- 时间复杂度 = O ( ∣ V ∣ + ∣ E ∣ ) = O(|V| + |E|) =O(∣V∣+∣E∣)
广度优先生成树
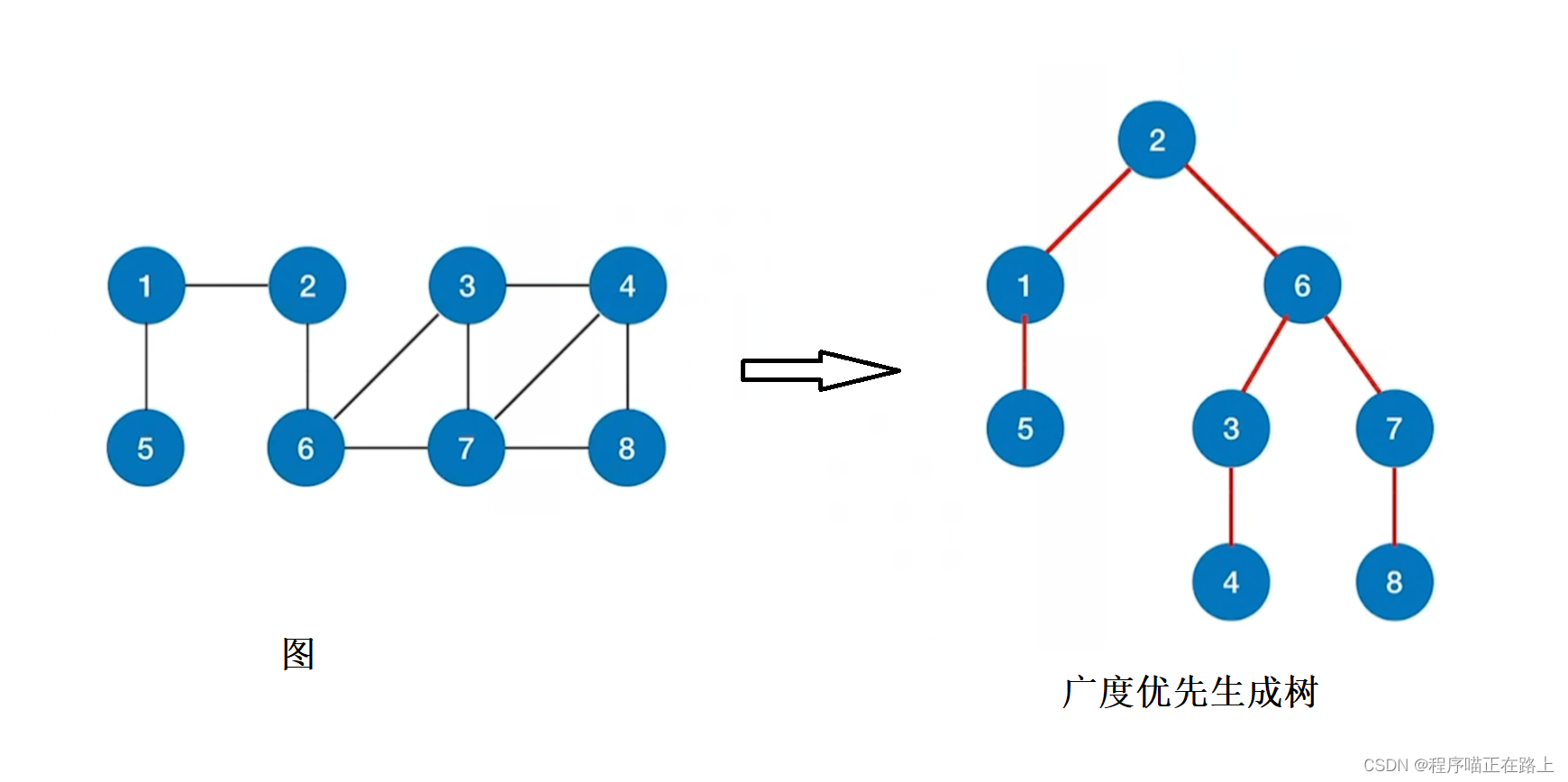
广度优先生成树由广度优先遍历过程确定。由于邻接表的表示方式不唯一,因此基于邻接表的广度优先生成树也不唯一
对于非连通图的广度优先遍历,我们还可以得到广度优先生成森林
深度优先遍历(DFS)
与树的深度优先遍历之间的联系
树的深度优先遍历分为先根遍历和后根遍历,图的深度优先遍历和树的先根遍历比较相似
//树的先根遍历
void PreOrder(TreeNode *R) {
if (R != NULL) {
visit(R); //访问根节点
while (R还有下一个子树T)
PreOrder(T); //先根遍历下一棵子树
}
}
算法实现
bool visited[MAX_VERTEX_NUM]; //访问标记数组
void DFSTraverse(Graph G) { //对图G进行深度优先遍历
for (v = 0; v < G.vexnum; ++v) //初始化已访问标记数据
visited[v] = false;
for (v = 0; v < G.vexnuj; ++v) //解决非连通图无法遍历完的问题
if (!visited[v]) DFS(G, v);
}
void DFS(Graph G, int v) { //从顶点v出发,深度优先遍历图G
visit(v); //访问顶点v
visited[v] = true; //设置已访问标记
for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
if (!visited[w]) { //w为v的未访问的邻接顶点
DFS(G, w);
}
}
}
复杂度分析
空间复杂度:来自函数调用栈,最坏情况下,递归深度为 O ( ∣ V ∣ ) O(|V|) O(∣V∣);最好情况为 O ( 1 ) O(1) O(1)
时间复杂度 = = = 访问每个节点所需时间 + + + 探索每条边所需时间
如果是用邻接矩阵存储的图:
- 访问 ∣ V ∣ |V| ∣V∣ 个顶点需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间
- 查找每个顶点的邻接点都需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间,总共有 ∣ V ∣ |V| ∣V∣ 个顶点
- 总时间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2)
如果是用邻接表存储的图:
- 访问 ∣ V ∣ |V| ∣V∣ 个顶点需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间
- 查找每个顶点的邻接点共需要 O ( ∣ E ∣ ) O(|E|) O(∣E∣) 的时间
- 时间复杂度 = O ( ∣ V ∣ + ∣ E ∣ ) = O(|V| + |E|) =O(∣V∣+∣E∣)
你会发现,深度优先遍历和广度优先遍历的复杂度是一样的
深度优先遍历序列
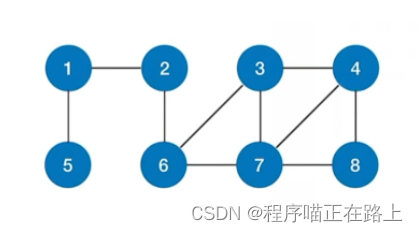
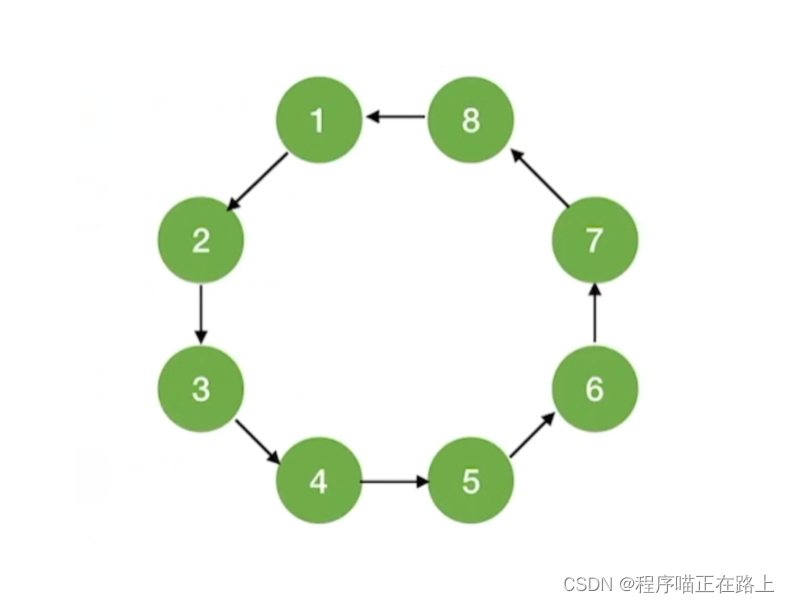
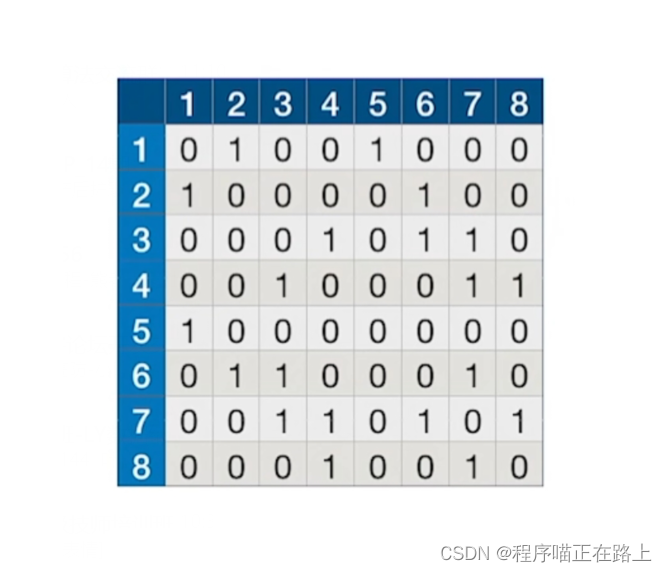
对于上图:
- 从 1 1 1 出发的深度优先遍历序列为: 1 , 2 , 6 , 3 , 4 , 7 , 8 , 5 1, 2, 6, 3, 4, 7, 8, 5 1,2,6,3,4,7,8,5
- 从 2 2 2 出发的深度优先遍历序列为: 2 , 1 , 5 , 6 , 3 , 4 , 7 , 8 2, 1, 5, 6, 3, 4, 7, 8 2,1,5,6,3,4,7,8
- 从 3 3 3 出发的深度优先遍历序列为: 3 , 4 , 7 , 6 , 2 , 1 , 5 , 8 3, 4, 7, 6, 2, 1, 5, 8 3,4,7,6,2,1,5,8
注意:如果邻接表不一样,深度优先遍历序列也可能不一样;同时,因为邻接矩阵表示方式唯一,所以深度优先遍历序列唯一
深度优先生成树
将深度优先遍历序列写成树的形式,即为对应的深度优先生成树
如果是非连通图,那么会有深度优先生成森林
图的遍历和图的连通性
对无向图进行 B F S / D F S BFS/DFS BFS/DFS 遍历,调用 B F S / D F S BFS/DFS BFS/DFS 函数的次数等于连通分量数;如果是连通图的话,我们只需要调用一次 B F S / D F S BFS/DFS BFS/DFS 函数
对有向图进行 B F S / D F S BFS/DFS BFS/DFS 遍历,调用 B F S / D F S BFS/DFS BFS/DFS 函数的次数要根据具体的数进行具体分析;如果起始顶点到其他顶点都有路径,那么我们只需要调用一次函数即可
对于强连通图,我们从任何一个顶点出发都只需要调用一次 B F S / D F S BFS/DFS BFS/DFS