1.马尔科夫链概述

假某一时刻的状态转移的概率只与它本身前一个状态有关，与前前一个、前前前一个状态都无关，用途：这样做可以大大简化模型的复杂度，因此马尔科夫链在时间序列模型中可以得到广泛的应用，比如循环神经网络RNN、隐式马尔科夫模型HMM、MCMC....

精确的数学定义：假设序列状态是 $\cdot \cdot \cdot X_{t-2},X_{t-1},X_{t},X_{t+1},\cdot \cdot \cdot$ ，那么在时刻 $X_{t+1}$ 的状态的条件概率仅仅依赖于前一个时刻 $X_{t}$ ，即：

$P(X_{t+1}|\cdot \cdot \cdot X_{t-2},X_{t-1},X_{t})=P(X_{t+1}|X_{t})$

既然某一时刻状态转移的概率只依赖于它的前一个状态，那么我们只要求出系统任意两个状态之间的转换概率，这个马尔科夫链的模型就确定下来了。

1.1股票市场模型

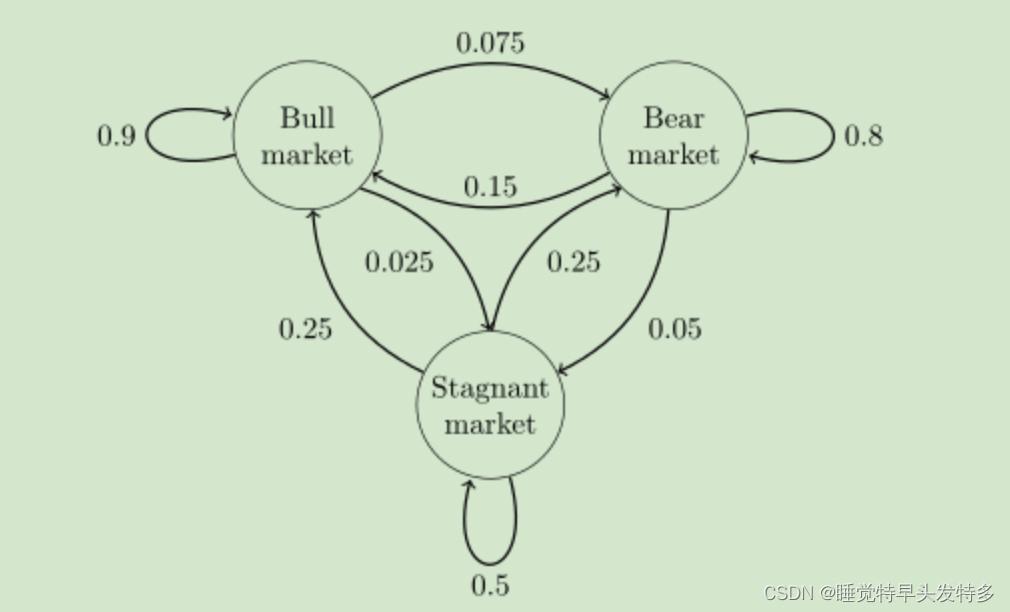
这个马尔科夫链是表示股市模型的，共有三种状态：牛市(Bull market)、熊市(Bear market)、横盘(Stagnant market) 。每一个状态都以一定的转换概率转化到下一个状态。

具体求解过程：http://t.csdn.cn/XVM6f

2.马尔科夫链模型状态转移矩阵的性质 (本节重点)

马尔科夫链模型的状态转移矩阵最终收敛得到的稳定概率分布与初始状态概率分布无关。用途：得到了这个稳定概率分布对应的马尔科夫链模型的状态转移矩阵，则我们可以用任意的概率分布样本开始，代入马尔科夫模型的状态转移矩阵，经过一些的序列的转换，最终可以得到符合对应稳定概率分布的样本。

这个性质不光对我们上面的状态转移矩阵有效，对于绝大多数的其他的马尔科夫链模型的状态转移矩阵也有效。同时不光是离散状态，连续状态时也成立。

对于一个确定的状态转移矩阵 $P$ ，它的n次幂 $P^{n}$ 在当n大于一定的值时，也可以发现是确定的概率分布。

2.1代码实例

import numpy as np
matrix =  np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]], dtype=float)
#vector1 = np.matrix([[0.7,0.1,0.2]], dtype = float)

for i in range(10):
    matrix = matrix*matrix
    print ("Current round:", i+1)
    print (matrix)

2.2实现结果

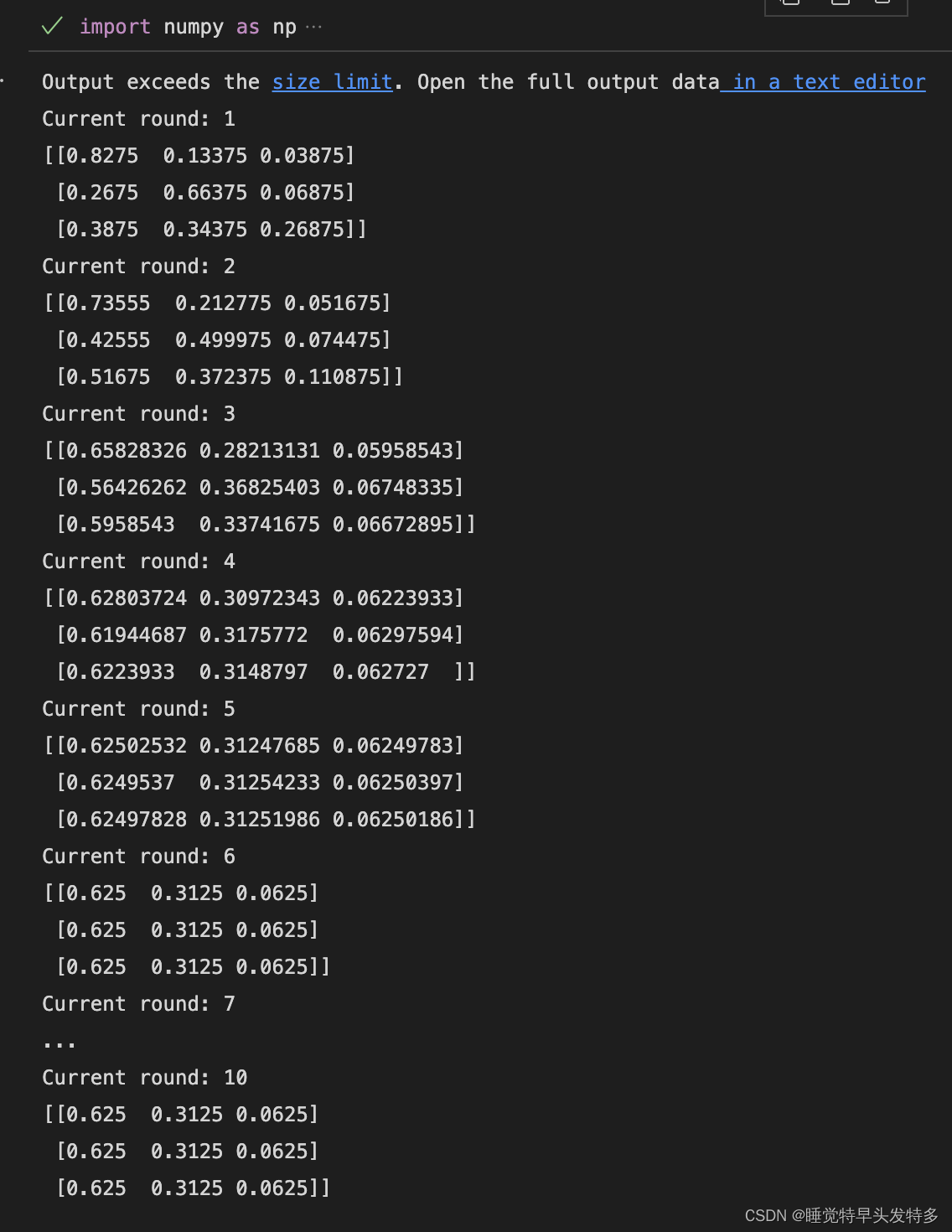
Current round: 1
[[0.8275 0.13375 0.03875]
[0.2675 0.66375 0.06875]
[0.3875 0.34375 0.26875]]
Current round: 2
[[0.73555 0.212775 0.051675]
[0.42555 0.499975 0.074475]
[0.51675 0.372375 0.110875]]
Current round: 3
[[0.65828326 0.28213131 0.05958543]
[0.56426262 0.36825403 0.06748335]
[0.5958543 0.33741675 0.06672895]]
Current round: 4
[[0.62803724 0.30972343 0.06223933]
[0.61944687 0.3175772 0.06297594]
[0.6223933 0.3148797 0.062727 ]]
Current round: 5
[[0.62502532 0.31247685 0.06249783]
[0.6249537 0.31254233 0.06250397]
[0.62497828 0.31251986 0.06250186]]
Current round: 6
[[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]]
Current round: 7
[[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]]
Current round: 8
[[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]]
Current round: 9
[[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]]
Current round: 10
[[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]
[0.625 0.3125 0.0625]]

我们可以发现，在 $n\geq 6$ 以后， $p^{n}$ 的值稳定不再变化，而且每一行都为[0.625 0.3125 0.0625]，这和我们前面的稳定分布是一致的，这个性质不光是离散状态成立，连续状态时也成立。

2.3马尔科夫链收敛性质总结

如果一个非周期的马尔科夫链有状态转移矩阵 $P$ ，并且它的任何两个状态是联通的，那么 $lim_{n\rightarrow \infty }P_{ij}^{n}$ 与i无关，我们有：

(1)

$lim_{n\rightarrow \infty }P_{ij}^{n}=\pi (j)$

(2)

$lim_{n\rightarrow \infty }P^{n}=\begin{pmatrix} \pi (1) &\pi (2) &... &\pi (j) &... \\ \pi (1) &\pi (2) &... & \pi (j) &... \\ ...& ... &... &... & ...\\ \pi (1) & \pi (2) & ... & \pi (j) &... \\ ... & ... &... &... & ... \end{pmatrix}$