【树状数组】前缀和问题

news2025/2/28 3:05:03

一、引子

给你一个数组 nums ，请你完成两类查询。

其中一类查询要求更新数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（包含）的nums元素的和

题目只是一个用来检测我们思想的东西，比如这道题它也不是前缀和呀？但是我们去仔细去想，区间和可以转化为两个前缀和相减

那可能有同学就要问了，为什么要用前缀和呀，我直接遍历求和不就可以了，是的，如果你的数据量非常小的情况下，是可以直接遍历求和，那你可以退出这篇文章，换言之，数组数组是为了解决大规模数据下的前缀和问题。那么，在我们了解了树状数组所要解决的问题之后，下面就要我们一起来看下树状数组是如何实现的？

二、树状数组

问题： 首先，我们思考一下如果在数据量大的情况下，如何减少遍历数组求前缀和的时间？

答：我们可以通过另一个数组记录前几个元素的和，比如记录下 1，2 和 2， 3 … 等等数组中元素的和，在求和时，直接拿之前求过的用就行了。

是的，树状数组就是这样一种思想，只不过它是以一种树状的结构将部分元素的前缀和存起来。

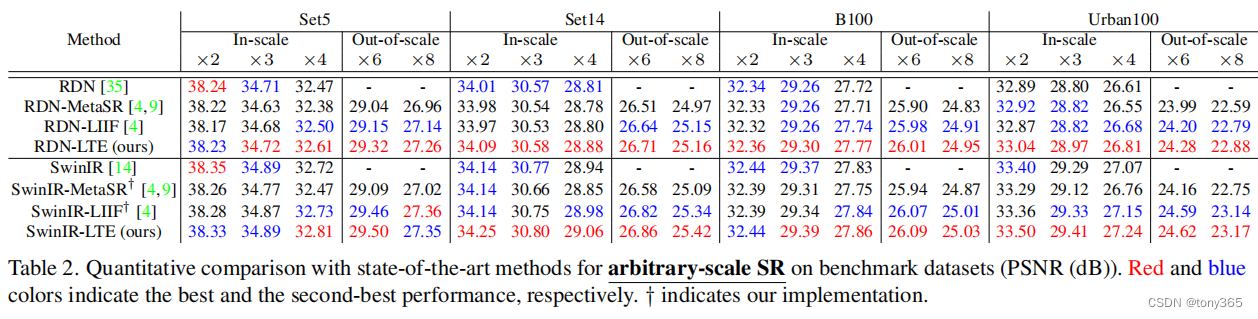
下图为构造前缀和树状数组图解，大家在看代码的同时，可以结合图解来看，助于理解。

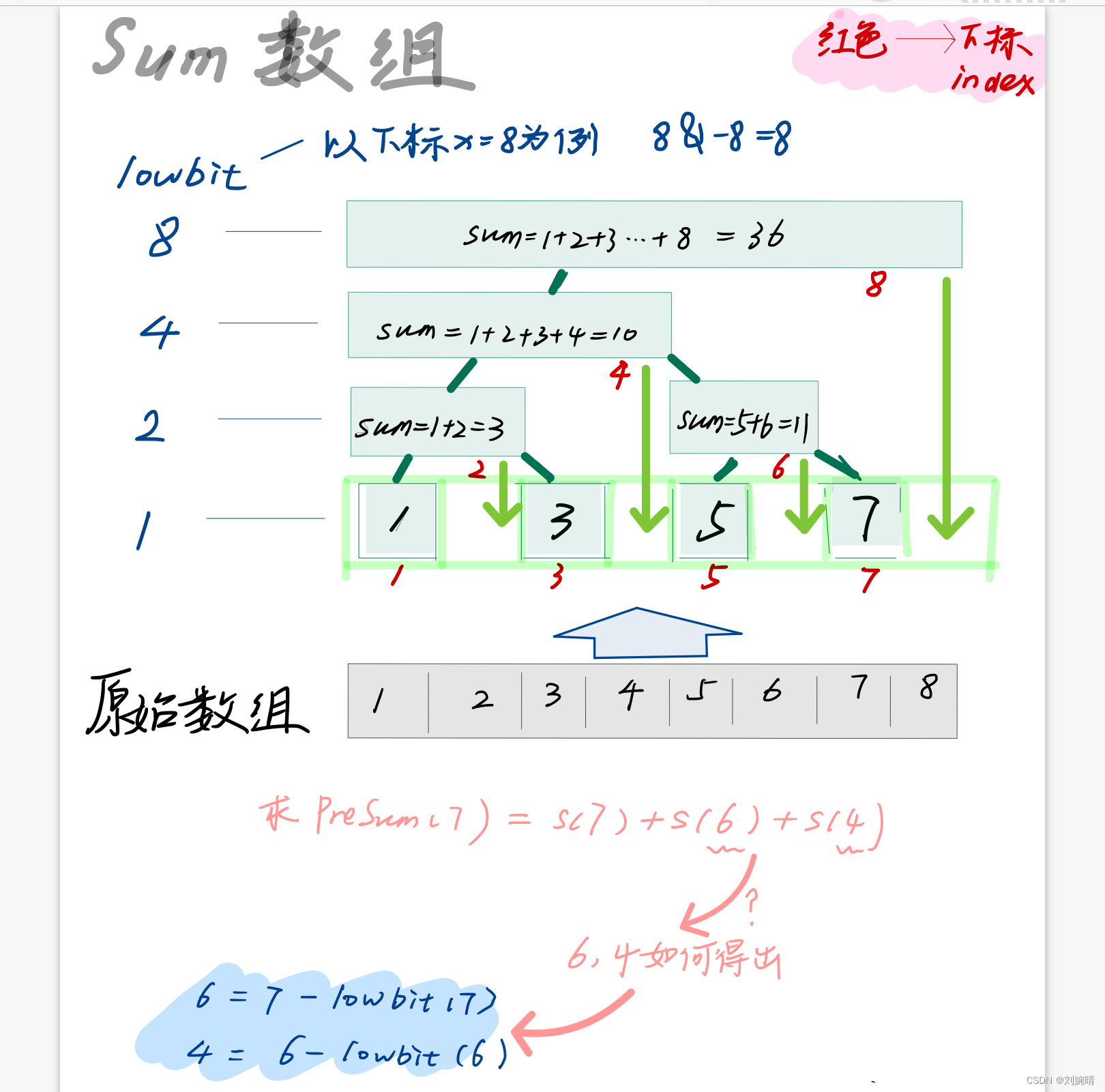
在这里插入图片描述

树状数组有四个关键部分组成，他们分别是：

lowbit 函数

lowbit函数结构如，其用来计算数组下标 x 的二进制表示的最后一个1及其后面的0组成的数是多少

        private int lowBit(int x) {
            return x & (-x);
        }

我们需要记住的是，通过 lowbit 函数计算出来的值在树状数组中可以用来表示(x 表示当前节点下标)：

1） 2 的当前节点在树中层数次幂 = lowbit(x)
2）当前节点在求前缀和时的下一个累加位置 = x - lowbit(x)

前缀和数组构造函数

在构造前缀和时，我们使用如下的构造函数：

		// 构造函数，用于初始化树状数组
        public NumArray(int[] nums) {
            // 原数组长度+1, +1的原因是计算lowbit时,使用下标0会进入死循环
            this.sums = new int[nums.length + 1];
            this.nums = nums;
            for (int i = 0; i < nums.length; i++) {
                // 初始化累加和数组
                insert(i, nums[i]);
            }
        }

     	// 插入方法
        private void insert(int index, int val) {
            // 下标+1
            int x = index + 1;
            while (x < sums.length) {
                sums[x] = sums[x] + val;
                x += lowBit(x);
            }
        }

query 查找函数

query 查找函数用于查找计算 x 位置前缀和需要累加的 sums 数组元素都有那些，对这步不理解的可以去看一下我图解中的那个例子

        /**
         * 查询树状数组， x 为查找的下标，返回值为计算好的前缀和
         */
        public int query(int x) {
            int s = 0;
            while (x != 0) {
                s += sums[x];
                x -= lowBit(x);
            }
            return s;
        }

前缀和数组更新函数

当我们更新某个节点值时，需要对前缀和数组进行更新，更新代码如下：

        /**
         * 更新数组以及累加和，index 为更新位置， val 为更新后的值
         */
        public void update(int index, int val) {
            int x = index + 1;
            while (x < sums.length) {
                // 减去之前nums[index]的值, 加上新的值
                sums[x] = sums[x] - nums[index] + val;
                x += lowBit(x);
            }
            nums[index] = val;
        }