快排排序是非常快的，但是有一种情况快排是无法进行的。

912. 排序数组 - 力扣（LeetCode）

这道题看上去没什么问题，但是如果我们用快排去提交的话，发现快排其实是被针对了的。

有一个样例是这样的。如果我们按照快排的思想，right指针将一路狂奔到left指针这里回合，然后每次分割区间都是只分割出去一个数，这样就会造成时间超限。

所以我们将快排进行优化，实现三路划分。

原来的快排思想是将小于等于key的放在左边，将大于等于key的放在右边，这样形成了两个区间。

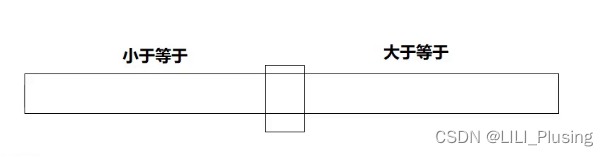
三路划分的思想其实就是，将小于key的放在左边，将大于key的放在右边，将等于key的放在中间。

然后分割区间的时候，左边小于key的一个，右边大于key的一个，中间的就不用再动了。

具体操作的方法：

还是left在左侧，right在右侧，current遍历。

当current遇到比key小的，就将current下的值和left交换，然后将left++，current++。（因为left为和key相等的值，交换过后left++，相当于是left左边是比key小的值，left永远指向和key相等的值）

当current遇到和key相等的值时，就将current++，继续遍历。

当current遇到比key大的值，就将current下的值和right交换，然后将right--（不先管right原位置的值的大小，先交换，此时right--后，right右侧的值则永远都是比key大的值，current不动，因为不确定交换后的值的大小。进行新一轮的比较之后，再决定去留）

代码：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 int GetMidIndex(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[right] < a[left])
		{
			return left;
		}
		else return right;
	}
	else
	{
		if (a[mid] > a[right])
			return mid;
		else if (a[left] < a[right])
			return left;
		else return right;
	}

}
 void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void QuickSort(int* a, int begin, int end)
{
    if (begin >= end)
	{  
		return;
	}
  int left = begin;
  int current = left+1;
  int right = end;
	int midi = GetMidIndex(a, left, right);
	Swap(&a[left], &a[midi]);
	int key = a[left];
	while (current <= right)
	{
		if(a[current] > key)
		{
			Swap(&a[current], &a[right]);
            right--;
		}
		else if(a[current] < key)
		{
            Swap(&a[current], &a[left]);
						left++;
						current++; 
		}
        else 
        current++;
	}
	QuickSort(a, begin,left-1);
	QuickSort(a, right+1, end);
}
int* sortArray(int* nums, int numsSize, int* returnSize){
    QuickSort(nums,0,numsSize-1);
    *returnSize = numsSize;
    return nums;
}

提交还有样例没过

做出三路划分后，这个样例针对的是快排的三数取中（GetMidIndex）方法。

但是如果去掉三数取中方法，当遇到接近有序的序列后就会超时。所以我们不能用普通的三数取中方法。

 int GetMidIndex(int* a, int left, int right)
{
	int mid = left+(rand()%(right-left));      //中间的数不再固定。
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[right] < a[left])
		{
			return left;
		}
		else return right;
	}
	else
	{
		if (a[mid] > a[right])
			return mid;
		else if (a[left] < a[right])
			return left;
		else return right;
	}

}

这样，这道题就可以用快排的方法提交了。