目录
一、点积
二、叉积
三、归一化
一、点积
点积,也称为内积或数量积,是一种用于计算两个向量之间关系的操作。对于两个三维向量 A(a1,a2,a3)和 B(b1,b2,b3),它们的点积可以用以下公式表示:
A·B=a1⋅b1+a2⋅b2+a3⋅b3

在UE中,点积运算可以用来判断两个向量之间的方向关系:
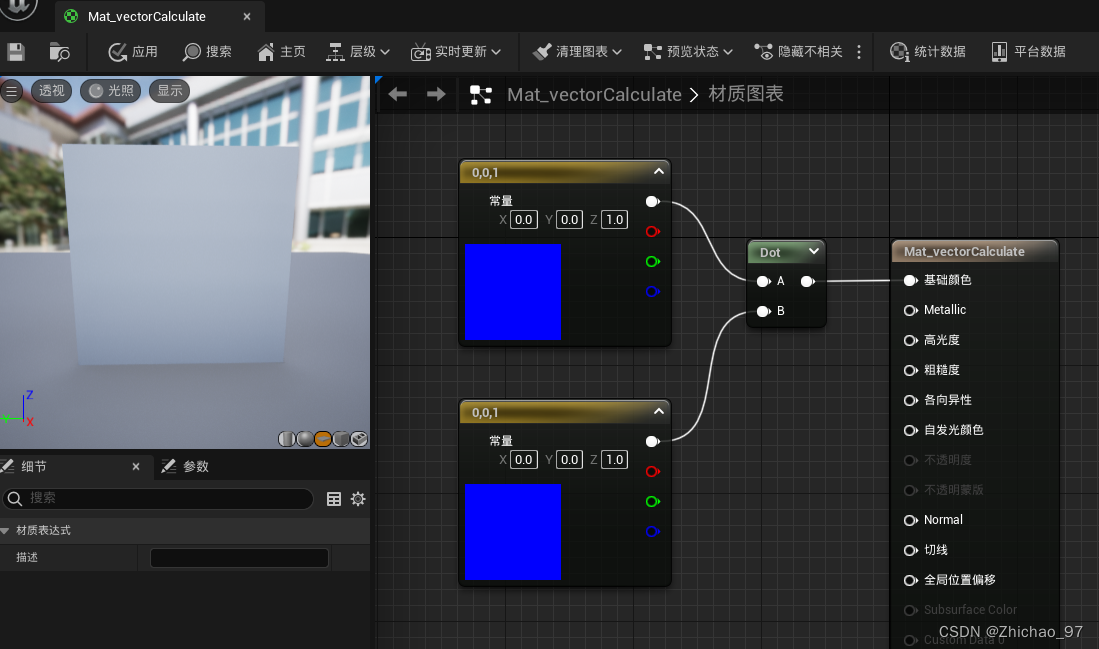
(1)方向相同,点积结果为1

如图,两个平行的沿Z轴方向的三维向量,做点积运算的结果是1
(2)方向垂直,点积结果为0

如图,两个互相垂直的三维向量,做点积运算的结果是0
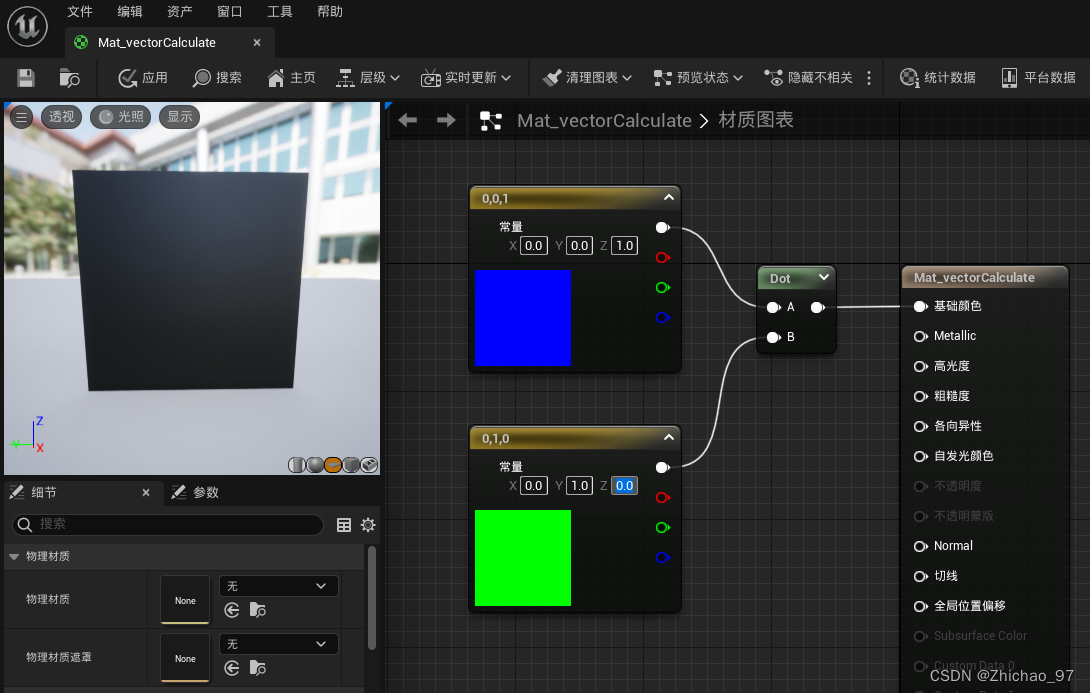
(3)方向反向,点积结果为-1

如图,两个方向相反的三维向量,做点积运算的结果是-1,由于颜色的范围是0~1,因此这里还是显示黑色
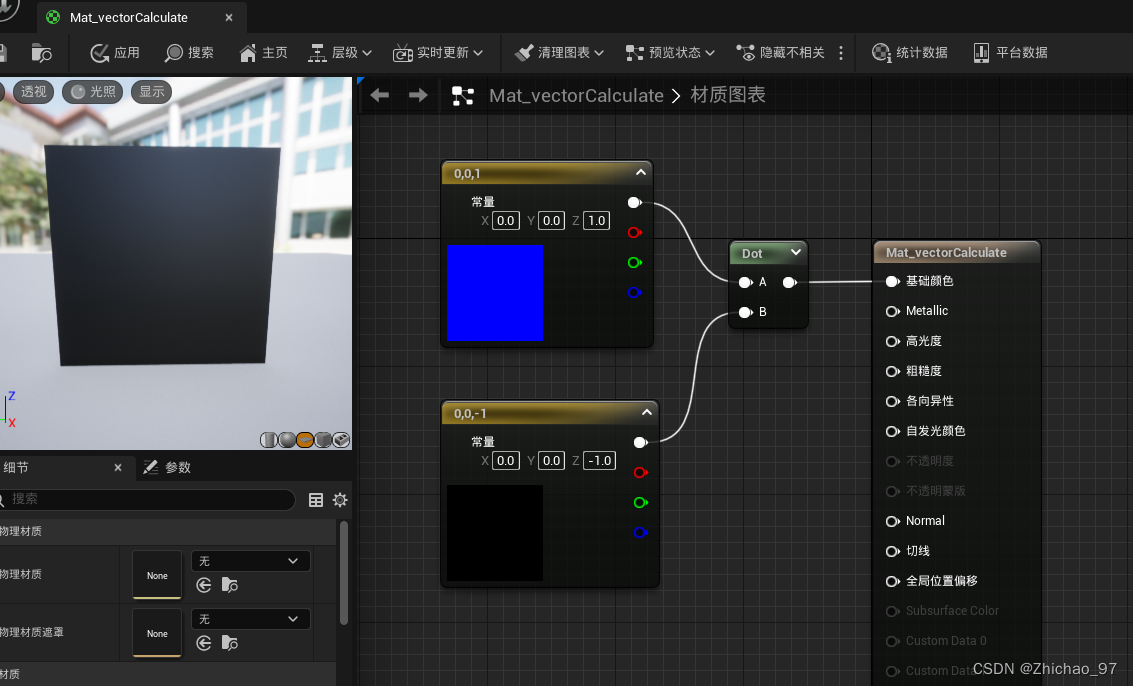
二、叉积
叉积,也称为外积或向量积,是一种用于计算两个向量之间关系的操作,产生一个新的向量。对于两个三维向量A(a1,a2,a3)和B(b1,b2,b3),它们的叉积可以用以下公式表示:
A×B=(a2b3−a3b2,a3b1−a1b3,a1b2−a2b1)
在UE中,叉积运算可以通过两个已知的轴向求得第三个轴向的运算

如图,(1,0,0)×(0,1,0)=(0,0,1),结果就是蓝色
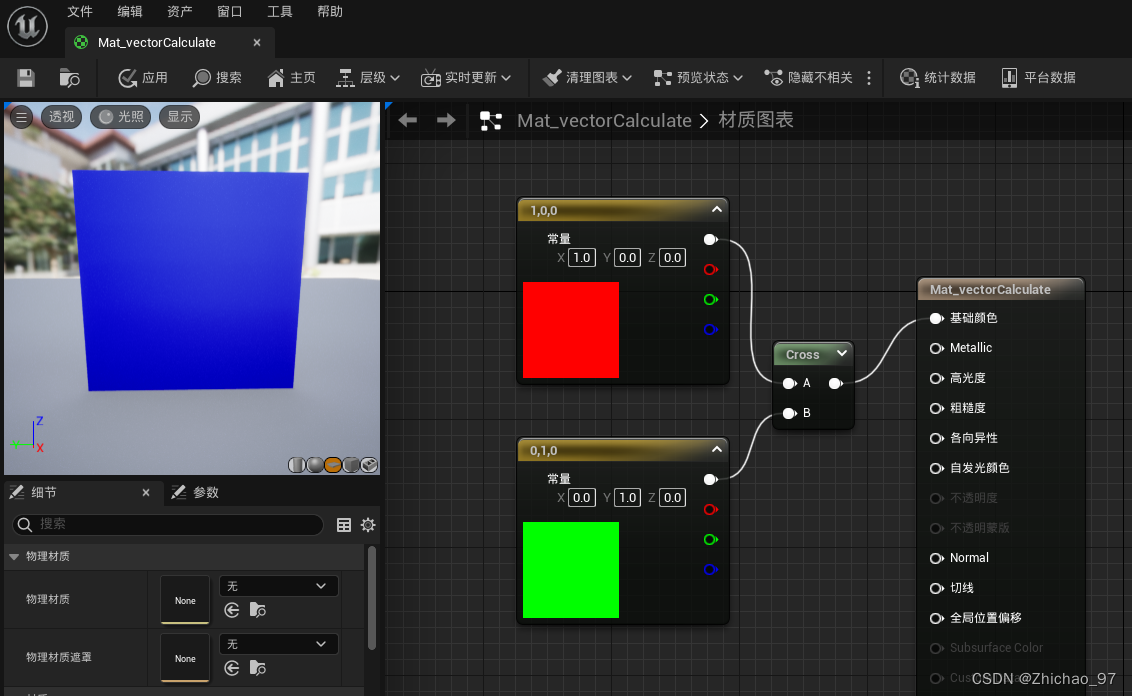
三、归一化
归一化是将一个向量或者数值进行缩放,使其长度(模)等于1,从而将其转化为单位向量或者标准化数值。
对于向量a,记|a|为a的模长, |a| = (向量a各分量二次幂相加结果)的开方,向量a的归一化记为a^ ,归一化后的a^又称向量a的 单位矢量,公式如下
a^ = a / |a|
在UE中,向量经过归一化运算后的向量只保留向量的方向信息,可以将向量长度统一设置为1

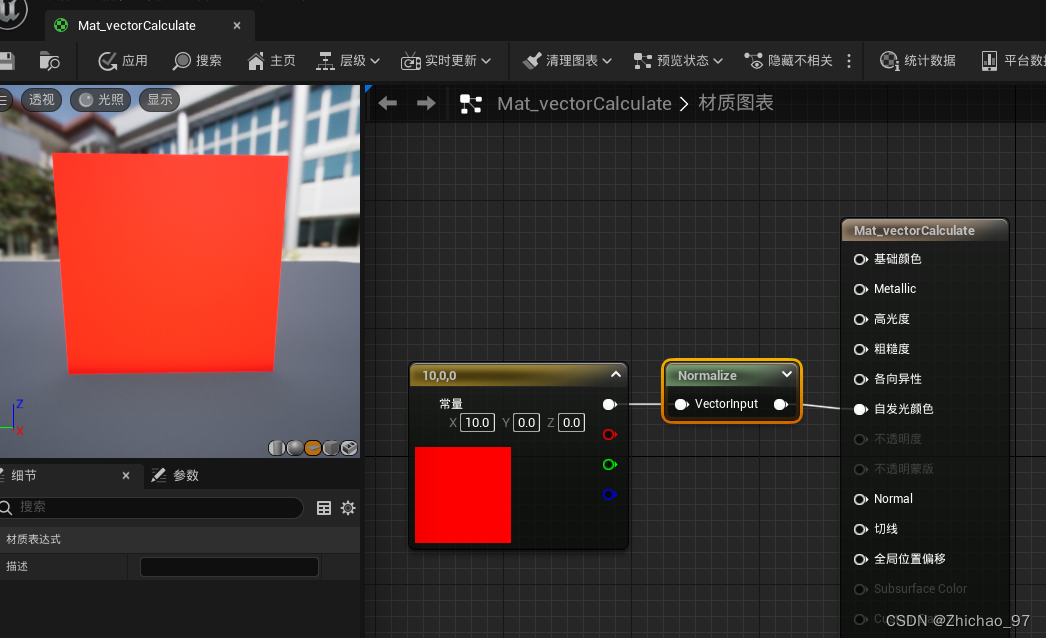
如下图,(10,0,0)会发出很亮的红光

经归一化后还原成(1,0,0)