---

前言

选择排序的基本思想就是每一次从待排序的数据元素中选出最小(或最大)的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

一、直接选择排序

1、直接选择排序基本思想

在元素集合array[i]–array[n-1]中选择值最大(小)的数据元素，若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换，在剩余的array[i]–array[n-2]（array[i+1]–array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素。
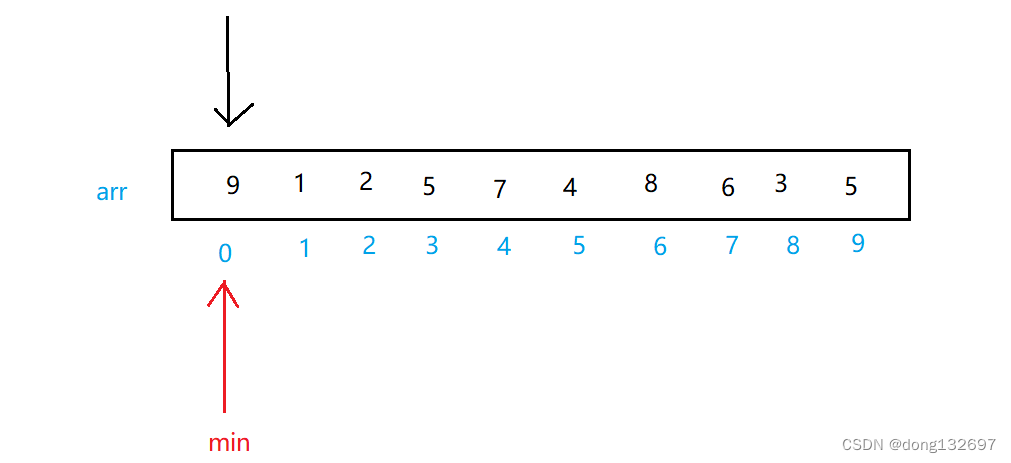
例如有如下一个数组。

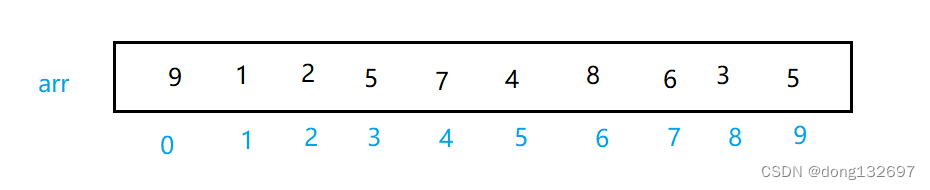
先取最小值min在数组中下标为0，然后遍历数组每个元素，并且使每个元素和下标为min的元素比较，如果该元素小于下标为min的元素，就使min等于该元素的下标，然后继续向后比较。


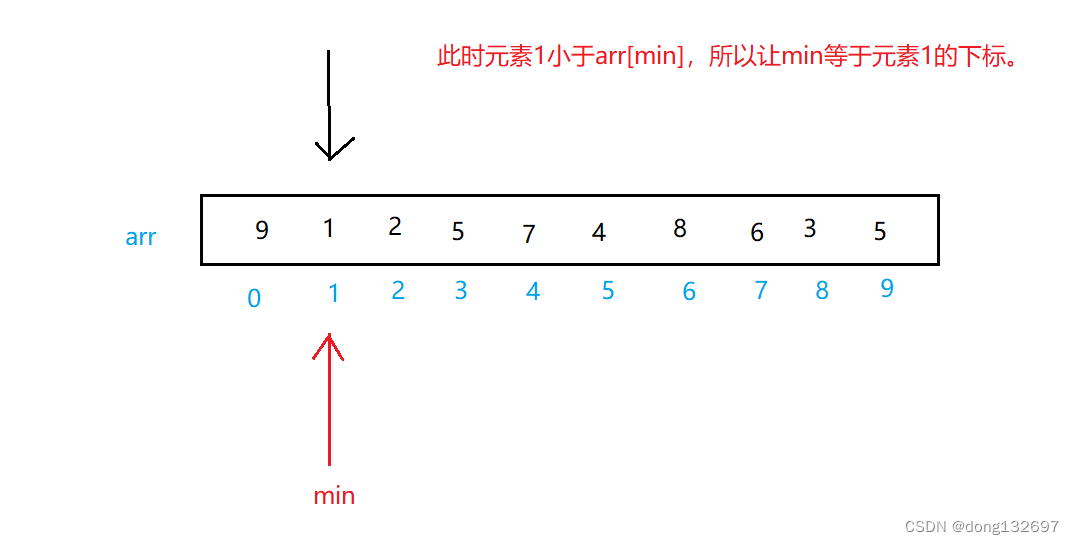
当遍历一遍数组后，此时下标为min的元素为数组中最小的元素。

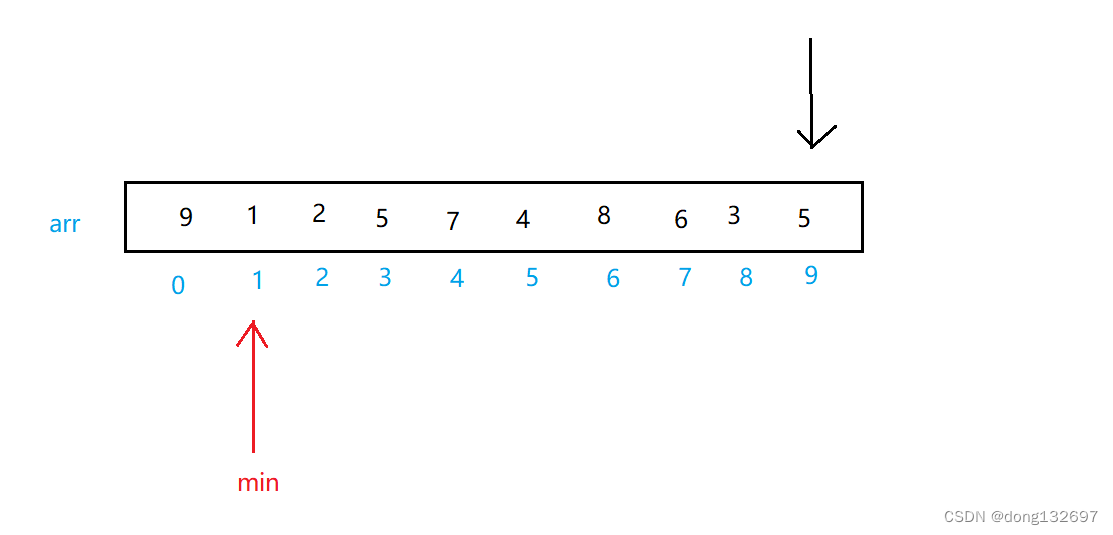
将下标为min的元素与下标为0的元素交换，使最小的元素在数组首位置，然后将min重新置为1，再次遍历数组寻找第二小的元素。

2、直接选择排序代码实现

在上述的演示中，每次遍历数组我们只找到了数组中未排序元素中最小的值，然后将该值放在排序好的元素之后。在代码实现时，我们稍微优化了一下，即定义min和max两个变量用来存数组中未排序元素中的最大值和最小值的下标，然后将最小值放在数组前面，最大值放在数组末尾。即每次遍历数组选择出最大值和最小值，然后放入相应的位置。

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void SelectSort(int* arr, int n)
{
	//记录数组的头尾下标
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		//另数组中未排序的首个元素的下标为未排序元素中的最大值和最小值
		int mini = begin;
		int maxi = begin;
		int i = 0;
		//从未排序的元素开始遍历数组
		for (i = begin+1; i <= end; i++)
		{
			//如果有元素比下标为mini的元素小，就让mini为该元素下标
			if (arr[i] < arr[mini])
			{
				mini = i;
			}
			//如果有元素比下标为maxi的元素大，就让max为该元素下标
			if (arr[i] > arr[maxi])
			{
				maxi = i;
			}
		}
		//然后将未排序中最小的元素和下标为begin的元素交换
		Swap(&arr[begin], &arr[mini]);
		//此时需要判断如果未排序中最大的元素的下标为begin的话，而执行过Swap(&arr[begin], &arr[mini]);语句后
		//原来begin下标的元素现在已经交换到下标为mini的位置了，所以此时未排序元素中最大的元素的下标为mini
		if (begin == maxi)
		{
			maxi = mini;
		}
		Swap(&arr[end], &arr[maxi]);
		++begin;
		--end;
	}
	
}

3、直接选择排序的效率

直接选择排序的复杂度为O(N²)，并且就算数组元素为基本顺序有序，直接选择排序的复杂度也为O(N²) 。而当数组元素为基本顺序有序时，直接插入排序的复杂度可以达到O(N)，并且只有数组元素逆序为直接插入排序的最差情况。所以综合考虑的话，直接选择排序的效率没有直接插入排序的高。

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

二、堆排序

1、堆排序

选择排序的基本思想就是每一次从待排序的数据元素中选出最小(或最大)的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。而堆结构的堆头结点存的就是整个堆中最大(最小)值，堆排序就是每次将堆中最大(最小)值取出，将堆头结点删除，再重新选出堆中最大(最小)值作为新堆头结点。所以堆排序也是选择排序的一种。
堆排序的详细讲解在下面这篇文章中，可以点击链接进行阅读。
c语言实现堆

2、堆排序的效率

1. 堆排序使用堆来选数，效率就高了很多。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定