目录
语法
说明
示例
求解具有实根的部分分式展开式
展开具有复数根和同次分子及分母的分式
展开分子次数高于分母次数的分式
residue函数的功能是部分分式展开(部分分式分解)。
语法
[r,p,k] = residue(b,a)
[b,a] = residue(r,p,k)说明
[r,p,k] = residue(b,a) 计算以如下形式展开的两个多项式之比的 部分分式展开式 的留数、极点和直项
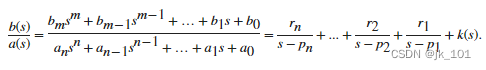
residue 的输入是由多项式 b = [bm ... b1 b0] 和 a = [an ... a1 a0] 的系数组成的向量。输出为留数 r = [rn ... r2 r1]、极点 p = [pn ... p2 p1] 和多项式 k。对于大多数教科书问题,k 为 0 或常量。
[b,a] = residue(r,p,k) 将部分分式展开式转换回两个多项式之比,并将系数返回给 b 和 a。
示例
求解具有实根的部分分式展开式
使用 residue 求以下多项式之比 F(s) 的部分分式展开式
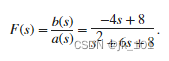
b = [-4 8];
a = [1 6 8];
[r,p,k] = residue(b,a)
r = 2×1
-12
8
p = 2×1
-4
-2
k =
[]此结果代表以下部分分式展开式
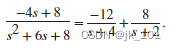
使用 residue 将部分分式展开转换回多项式系数。
[b,a] = residue(r,p,k)
b = 1×2
-4 8
a = 1×3
1 6 8
此结果表示初始分式 F(s)。
展开具有复数根和同次分子及分母的分式
如果分子的次数与分母的次数相等,输出 k 可以是非零值。
求解具有复数根和同次分子和分母的两个多项式 F(s) 之比的部分分式展示式,其中 F(s) 为
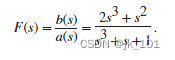
b = [2 1 0 0];
a = [1 0 1 1];
[r,p,k] = residue(b,a)
r = 3×1 complex
0.5354 + 1.0390i
0.5354 - 1.0390i
-0.0708 + 0.0000i
p = 3×1 complex
0.3412 + 1.1615i
0.3412 - 1.1615i
-0.6823 + 0.0000i
k = 2residue 返回代表部分分式展开式的复数根和极点,以及常项 k
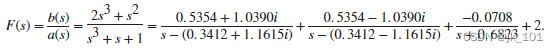
展开分子次数高于分母次数的分式
当分子次数大于分母次数时,输出 k 为代表 s 中多项式系数的向量。
使用 residue 执行 F(s) 的以下部分分式展开式。
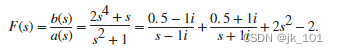
b = [2 0 0 1 0];
a = [1 0 1];
[r,p,k] = residue(b,a)
r = 2×1 complex
0.5000 - 1.0000i
0.5000 + 1.0000i
p = 2×1 complex
0.0000 + 1.0000i
0.0000 - 1.0000i
k = 1×3
2 0 -2
k 代表多项式![]()
参数说明:
b — 分子多项式的系数
a — 分母多项式的系数
r — 部分分式展开式残差
p — 部分分式展开式的极点
k — 直项(直项,以数字行向量的形式返回,这些数字按 s 的降幂指定多项式的系数。)