两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

示例 1：

输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑
上面的箭头指出了对应二进制位不同的位置。

示例 2：

输入：x = 3, y = 1
输出：1

提示：

• 0 <= x, y <= 231 - 1

一、信息

1.汉明距离的定义汉明距离指的是这两个数字对应二进制位不同的位置的数目

2.给我两个整数x和y,计算并返回它们的汉明距离

二、分析

条件1：如果只看条件1那么我会困惑，但是题目给出的示例1和2已经告诉我其实这道题就是数两个二进制数比较位数不相同的个数。

条件2：本题的目的

三、步骤

第一步接收 两个整数

第二步然后把两个整数转化为二进制

第三步逐列比较字符的是否相同如果相同就在累加器中++否则就不做处理

第四步输出累加器中的值

四、实现：

1.第一步 可以通过C语言中可以用scanf函数C++中可以用cin函数

问题出现：

第二步该如何将10进制整型数转化为2进制呢？

第三步 1.该如何逐列比较二进制呢（2.该如何实现移位呢？）

第四步 可以通过printf 

第五步：我的解答

第二步的思路

我想到了 种办法

第一条路 就是通过辗转相除法

第二条路 英雄师傅的路就是通过异或运算这样C系统就会自动把异或两边的数装化为二进制

第三步 

我想到了 种办法

第一条路就是直接比较ASCII

第二条路 异或直接通过移位运算符号

六、代码实现

我的答案：

我的答案：

首先，我们可以使用异或操作来找出两个数字中不同的位。异或操作的结果是，如果两个位不同，则该位为1；如果两个位相同，则该位为0。然后，我们可以计算结果中1的个数，这就是两个数字的汉明距离。

以下是用C语言和C++分别实现的方法：

C语言实现：

#include <stdio.h>

int hammingDistance(int x, int y) {
    int xorResult = x ^ y;
    int count = 0;
    while (xorResult) {
        count += xorResult & 1;
        xorResult >>= 1;
    }
    return count;
}

int main() {
    int x, y;
    x = 1;
    y = 4;
    printf("Hamming distance between %d and %d is: %d\n", x, y, hammingDistance(x, y));
    x = 3;
    y = 1;
    printf("Hamming distance between %d and %d is: %d\n", x, y, hammingDistance(x, y));
    return 0;
}

C++实现：

#include <iostream>
using namespace std;

int hammingDistance(int x, int y) {
    int xorResult = x ^ y;
    int count = 0;
    while (xorResult) {
        count += xorResult & 1;
        xorResult >>= 1;
    }
    return count;
}

int main() {
    int x, y;
    x = 1;
    y = 4;
    cout << "Hamming distance between " << x << " and " << y << " is: " << hammingDistance(x, y) << endl;
    x = 3;
    y = 1;
    cout << "Hamming distance between " << x << " and " << y << " is: " << hammingDistance(x, y) << endl;
    return 0;
}

这两种实现方法的逻辑是一样的，只是语言不同。

英雄师傅答案：

int hammingDistance(int x, int y){
    int z=x^y;
    int c=0;
    while(z){
        if(z&1){
            ++c;
        }
        z>>=1;
    }
    return c;
}

Leetcode答案：

C语言：

方法一：内置位计数功能

思路及算法

大多数编程语言都内置了计算二进制表达中 111 的数量的函数。在工程中，我们应该直接使用内置函数。

代码

int hammingDistance(int x, int y) {
    return __builtin_popcount(x ^ y);
}

复杂度分析

时间复杂度：O(1)O(1)O(1)。不同语言的实现方法不一，我们可以近似认为其时间复杂度为 O(1)O(1)O(1)。

空间复杂度：O(1)O(1)O(1)。

C++：

class Solution {
public:
    int hammingDistance(int x, int y) {
        return __builtin_popcount(x ^ y);
    }
};

方法二：移位实现位计数
思路及算法

在锻炼算法能力时，重复造轮子是不可避免的，也是应当的。因此读者们也需要尝试使用各种方法自己实现几个具有位计数功能的函数。本方法将使用位运算中移位的操作实现位计数功能。

具体地，记 s=x⊕ys = x \oplus ys=x⊕y，我们可以不断地检查 sss 的最低位，如果最低位为 111，那么令计数器加一，然后我们令 sss 整体右移一位，这样 sss 的最低位将被舍去，原本的次低位就变成了新的最低位。我们重复这个过程直到 s=0s=0s=0 为止。这样计数器中就累计了 sss 的二进制表示中 111 的数量。

C语言：

int hammingDistance(int x, int y) {
    int s = x ^ y, ret = 0;
    while (s) {
        ret += s & 1;
        s >>= 1;
    }
    return ret;
}

C++：

class Solution {
public:
    int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while (s) {
            ret += s & 1;
            s >>= 1;
        }
        return ret;
    }
};

复杂度分析

时间复杂度：O(log⁡C)O(\log C)O(logC)，其中 CCC 是元素的数据范围，在本题中 log⁡C=log⁡231=31\log C=\log 2^{31} = 31logC=log2 
31
 =31。

空间复杂度：O(1)O(1)O(1)。

方法三：Brian Kernighan 算法
思路及算法

在方法二中，对于 s=(10001100)2s=(10001100)_2s=(10001100) 2的情况，我们需要循环右移 888 次才能得到答案。而实际上如果我们可以跳过两个 111 之间的 000，直接对 111 进行计数，那么就只需要循环 333 次即可。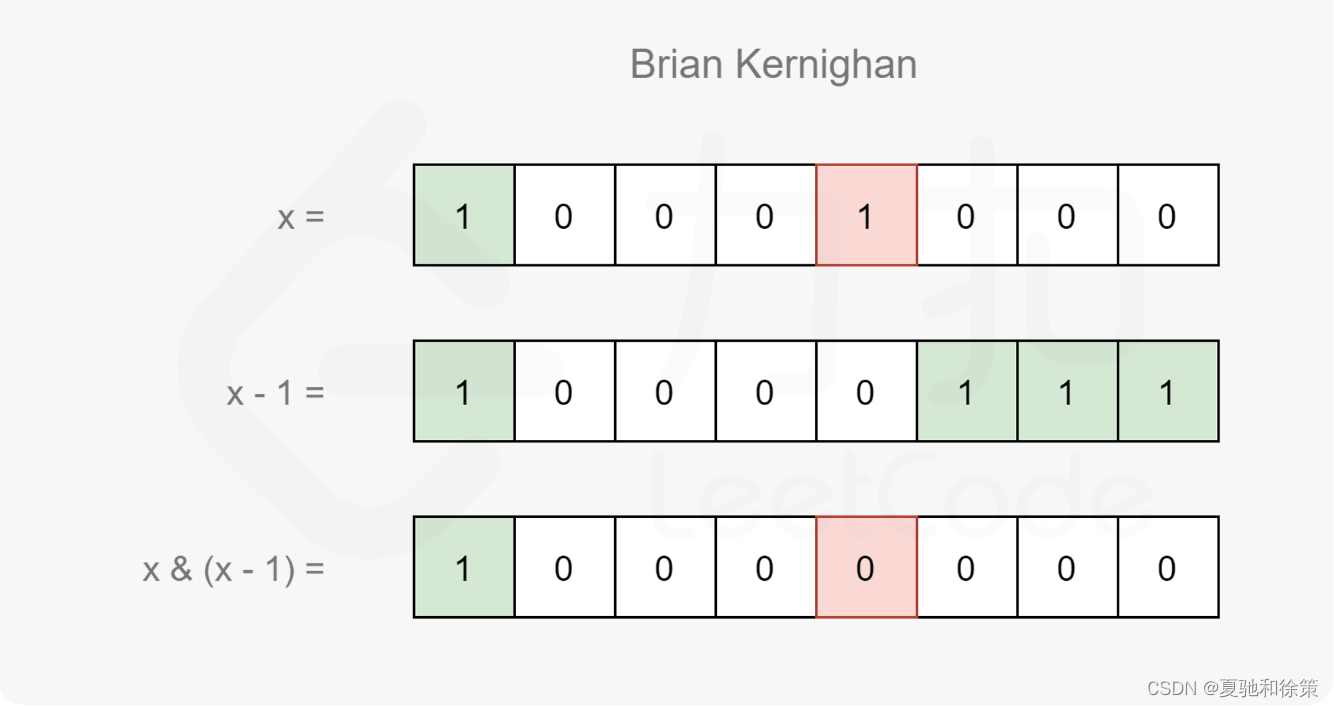

我们可以使用 Brian Kernighan 算法进行优化，具体地，该算法可以被描述为这样一个结论：记 f(x)f(x)f(x) 表示 xxx 和 x−1x-1x−1 进行与运算所得的结果（即 f(x)=x & (x−1)f(x)=x~\&~(x-1)f(x)=x & (x−1)），那么 f(x)f(x)f(x) 恰为 xxx 删去其二进制表示中最右侧的 111 的结果。

C语言：

int hammingDistance(int x, int y) {
    int s = x ^ y, ret = 0;
    while (s) {
        s &= s - 1;
        ret++;
    }
    return ret;
}

C++：
 

class Solution {
public:
    int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while (s) {
            s &= s - 1;
            ret++;
        }
        return ret;
    }
};

总结：

### 步骤总结：

1. **输入**：通过C语言的`scanf`函数或C++的`cin`函数进行整数输入。

2. **整型数转为二进制**：
   - **问题**: 如何将10进制整型数转化为2进制？
   - **我的解答**：
      1. 使用**辗转相除法**。这种方法通过不断地除以2并记录余数，可以得到整数的二进制表示。但这个方法比较繁琐。
      2. 利用**异或运算**。异或会直接对整数的二进制表示进行操作。例如，进行`x ^ y`操作，C/C++ 会自动把`x`和`y`转化为二进制后再进行运算。

3. **逐列比较二进制**：
   - **问题**: 1. 如何逐列比较二进制？2. 如何实现移位？
   - **我的解答**：
      1. 通过直接比较ASCII码。但这实际上不是一个适合比较整数二进制位的方法。
      2. 使用**异或运算**后，再通过**移位运算符**逐位检查异或的结果，可以得到不同的二进制位的数量。

4. **输出**：可以通过`printf`函数进行输出。

### 反思：

在解决这个问题时，我的初步思路围绕了如何将整数转化为其二进制表示并逐列比较。然而，经过进一步的考虑和查看其他答案，我意识到直接使用异或和移位操作可以更加简洁和高效地解决这个问题。

英雄师傅的答案使用了异或操作来直接找出两个整数在二进制表示中不同的位，并使用移位操作来计算这些位的数量。这种方法避免了将整数显式转化为其二进制字符串表示的需要，并提供了一个更直接和高效的解决方案。

在解决此类问题时，考虑问题的本质和使用适当的工具是关键。通过反思，我认识到在处理与二进制位操作相关的问题时，应当更多地考虑位操作符，如异或、与、或和移位，这些操作符为我们提供了直接操作整数二进制位的能力。

Leetcode题解提供了几种求汉明距离的方法，包括使用内置函数、移位实现和Brian Kernighan算法。

### 步骤总结：

1. **输入**：可以通过C语言中的`scanf`函数或C++中的`cin`函数进行输入。

2. **整型数转为二进制**：
   - **问题**: 如何将10进制整型数转化为2进制？
   - **我的解答**：
      1. 使用**辗转相除法**。
      2. 利用**异或运算**。
   - **Leetcode的解答**：没有显式转换为二进制。而是通过异或运算`x ^ y`得到两个数字的不同位，然后计算这个结果中1的数量。

3. **逐列比较二进制**：
   - **问题**: 1. 如何逐列比较二进制？2. 如何实现移位？
   - **我的解答**：
      1. 通过直接比较ASCII码。
      2. 使用**异或运算**后，再通过**移位运算符**逐位检查。
   - **Leetcode的解答**：使用异或运算后，通过以下几种方法计算1的数量：
      1. 使用内置函数`__builtin_popcount`。
      2. 使用移位操作。
      3. 使用Brian Kernighan算法。

4. **输出**：可以通过C语言中的`printf`函数或C++中的`cout`函数进行输出。

### 反思：

从Leetcode的答案中，我认识到计算汉明距离的方法可以非常简洁和高效。不需要显式地转换整数为其二进制字符串表示。异或运算和位操作是解决此类问题的关键。

通过对比不同的解法，我明白了在解决算法问题时，不仅要找到一个解决方案，而且要找到最优和最简洁的方法。在未来，我应该更多地考虑和熟悉位操作，这样可以更快速和有效地解决与二进制操作相关的问题。

学到了什么？

Brian Kernighan算法是用于计算一个二进制数中`1`的个数的一种高效方法，也被称为Kernighan技巧或Kernighan方法。这个算法的名字来源于Brian W. Kernighan，他是计算机科学的著名人物，并不是因为他发明了这个算法，而是因为这个技巧在他与Ritchie合著的经典书籍《C编程语言》中被提及。

### 算法核心：

Kernighan算法的主要思路是利用一个关键的位操作技巧：对于任意整数`n`，执行`n & (n - 1)`会把`n`的最低位的`1`变为`0`。

### 步骤：

1. 初始化计数器为0。
2. 当`n`不为0时，执行以下操作：
   1. 执行`n = n & (n - 1)`。
   2. 计数器增加1。

当`n`变为0时，计数器的值就是`n`的二进制表示中`1`的个数。

### 例子：

假设`n = 12`，它的二进制表示是`1100`。

1. 执行`n & (n - 1)`：`1100 & 1011` = `1000`，计数器加1。
2. 再次执行：`1000 & 0111` = `0000`，计数器加1。

最后，计数器的值为2，与`1100`中`1`的个数相匹配。

### 优点：

相比于简单地逐位检查，Kernighan算法更加高效，因为它只执行了与`n`的二进制中`1`的数量相同次数的操作，而不是总的位数次。