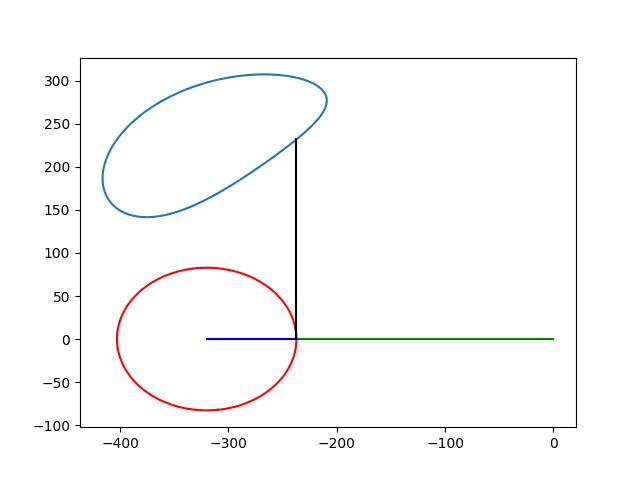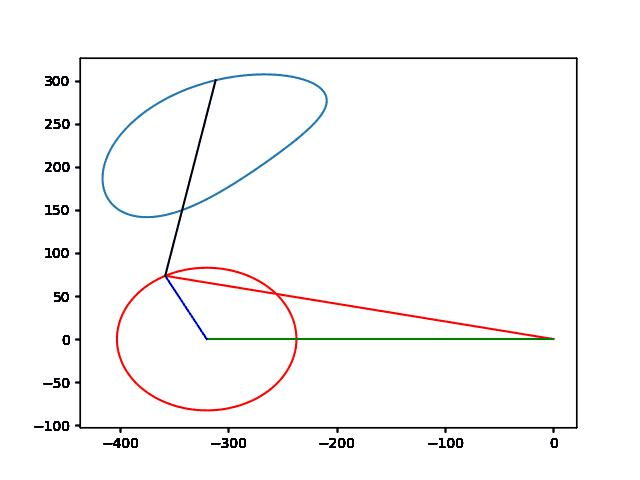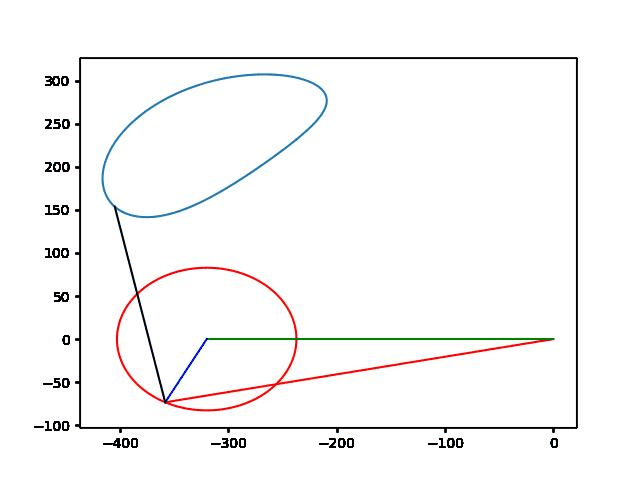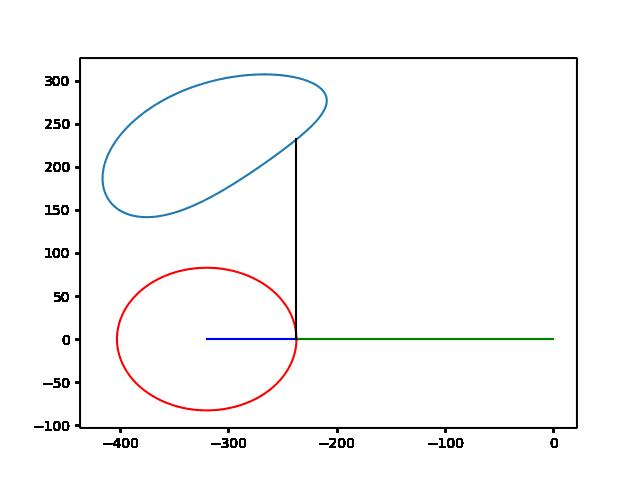
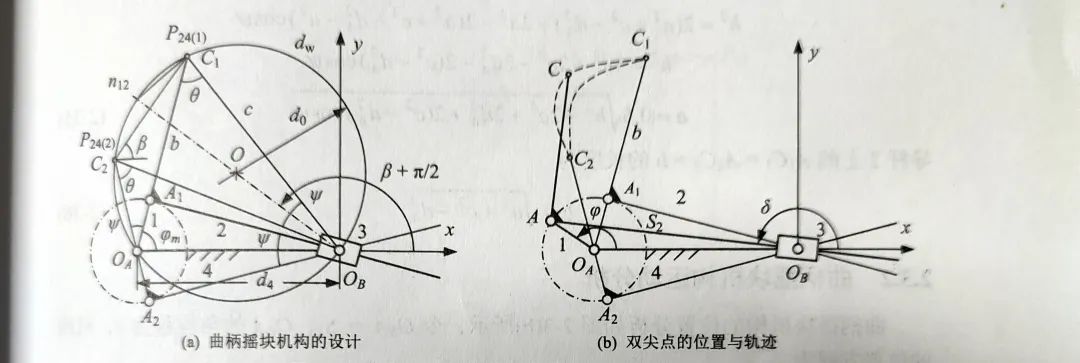
曲柄摇块机构是一种常用的平面连杆机构,由曲柄、摇块和连杆组成。其中,曲柄是主动件,通常为等速转动,摇块为从动件,在曲柄的转动下作往复摆动。摇块机构可以将曲柄的旋转运动转化为摇块的往复运动,也可以将摇块的摆动转化为曲柄的转动。
摇块机构广泛应用于机械传动和运动控制领域,如机床、自动化设备、汽车等。其优点是结构简单、运动平稳、传动效率高,缺点是存在惯性力和摩擦损失,需要进行适当的设计和调整。
在摇块机构中,固定件可以选择连杆、导杆等不同形式,从而演化出多种变体机构。例如,曲柄摇杆机构、曲柄滑块机构等。摇块机构还可以与其他机构组合使用,如与凸轮机构组合可以实现更复杂的运动轨迹。
在曲柄摇块机构中,导杆是一种常见的固定件,通常用于连接曲柄和摇块,使它们能够相互转动。导杆上的双尖点轨迹是指在摇块运动的过程中,导杆上的两个尖点所形成的轨迹。
导杆上的双尖点轨迹是曲柄摇块机构运动学特性的重要表现形式之一。通过研究导杆上的双尖点轨迹,可以分析摇块机构的运动规律和性能特点,为摇块机构的设计和优化提供依据。
1、生成单张图片
import sympy as sy
import numpy as np
import matplotlib.pyplot as plt
import imageio
x1,y1,x2,y2,pu,fi= sy.symbols('x1,y1,x2,y2,pu,fi')
h=sy.sqrt((x1-x2)**2+(y1-y2)**2)
c=0.5*h/sy.sin(0.5*pu)
beta=sy.atan((y1-y2)/(x1-x2))
d0=0.5*h/(sy.sin(0.5*pu)*sy.cos(0.5*pu))
x0=0.5*d0*sy.cos(beta+sy.pi/2)
y0=0.5*d0*sy.sin(beta+sy.pi/2)
d4=sy.sqrt(0.25*d0**2-y0**2)-x0
a=0.5*sy.sqrt(h**2-2*c**2+2*d4**2+2*(c**2-d4**2)*sy.cos(pu))
b=sy.sqrt(a**2+c**2-d4**2)
delta=sy.atan(a*sy.sin(fi)/(a*sy.cos(fi)-d4))+sy.pi
S2=sy.sqrt((a*sy.sin(fi))**2+(a*sy.cos(fi)-d4)**2)
xp=-d4+a*sy.cos(fi)+b*sy.cos(delta-sy.pi/2)
yp=a*sy.sin(fi)+b*sy.sin(delta-sy.pi/2)
xp_c=xp.subs({x1:-240,y1:305,x2:-360,y2:145,pu:30*sy.pi/180})
yp_c=yp.subs({x1:-240,y1:305,x2:-360,y2:145,pu:30*sy.pi/180})
# sy.plot_parametric(xp_c,yp_c,(fi,0,2*sy.pi))
fi_v=90*np.pi/180
fd4=d4.subs({x1:-240,y1:305,x2:-360,y2:145,pu:30*sy.pi/180})
fdelta=delta.subs({x1:-240,y1:305,x2:-360,y2:145,pu:30*sy.pi/180})
fa=a.subs({x1:-240,y1:305,x2:-360,y2:145,pu:30*sy.pi/180})
fb=b.subs({x1:-240,y1:305,x2:-360,y2:145,pu:30*sy.pi/180})
fS2=S2.subs({x1:-240,y1:305,x2:-360,y2:145,pu:30*sy.pi/180})
fdelta_c=sy.lambdify(fi, fdelta, modules='numpy')
fa_c=sy.lambdify(fi, fa, modules='numpy')
fb_c=sy.lambdify(fi, fb, modules='numpy')
fS2_c=sy.lambdify(fi, fS2, modules='numpy')
xx=sy.lambdify(fi, xp_c, modules='numpy')
yy=sy.lambdify(fi, yp_c, modules='numpy')
tt=np.linspace(0,np.pi*2,num=100)
fig = plt.figure()
for fi_v in np.linspace(0,np.pi*2,num=50):
# 1.圆半径
r = fa_c(fi_v)
# 2.圆心坐标
a, b = (-float(fd4), 0.)
# ==========================================
# 参数方程画圆形
theta = np.arange(0, 2 * np.pi, 0.01)
x = a + r * np.cos(theta)
y = b + r * np.sin(theta)
ax = fig.add_subplot()
ax.plot(x, y, c='red')
ax.plot(xx(tt), yy(tt))
# OB-A
ax.plot([0, -float(fd4) + fa_c(fi_v) * np.cos(fi_v)], [0, fa_c(fi_v) * np.sin(fi_v)], c='r')
# OA-OB
ax.plot([0, -float(fd4)], [0, 0], c='g')
# OA-A
ax.plot([-float(fd4) + fa_c(fi_v) * np.cos(fi_v), -float(fd4)], [fa_c(fi_v) * np.sin(fi_v), 0], c='b')
# A-C
pax = -float(fd4) + fa_c(fi_v) * np.cos(fi_v)
pay = fa_c(fi_v) * np.sin(fi_v)
pcx = xx(fi_v)
pcy = yy(fi_v)
ax.plot([pax, pcx], [pay, pcy], c='k')
plt.savefig("%.2f.jpg" % fi_v)
2、图片合成gif
import glob
from PIL import Image
img = glob.glob('*.jpg')
imgs = []
for i in img:
temp = Image.open(i)
imgs.append(temp)
imgs[0].save('road.gif', save_all=True, append_images=imgs, duration=500)