15-数据结构-二叉树的遍历，递归和非递归

news2024/11/19 18:25:45

简介：
        本文主要是代码实现，二叉树遍历，递归和非递归（用栈）。主要为了好理解，直接在代码处，加了详细注释，方便复习和后期默写。主要了解其基本思想，为后期熟练应用打基础。

遍历的意义，就是为了实现在二叉树上，进行各种操作，给每个结点都光顾到位，到根节点时，进行当前节点的操作。

目录：

目录

一、前序遍历。

1.1前序遍历—递归

1.2前序遍历—非递归

二、中序遍历

2.1中序遍历—递归

2.2中序遍历—非递归

三、后序遍历

3.1后序遍历—递归

3.2后序遍历—非递归

   五、总代码

5.1代码

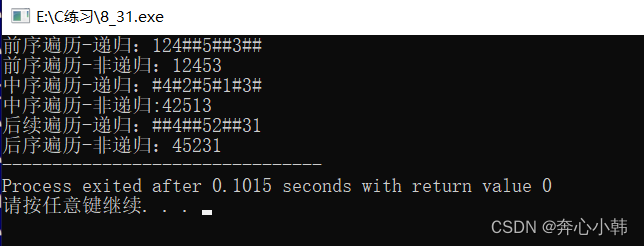
5.2运行结果图

一、前序遍历。

1.1前序遍历—递归

        简介：前序为：先访问根结点，再访问其左孩子，再访问右孩子（根左右）。

//前序遍历，递归 
void PreOrder(BTNode *node)
{
	if(node==NULL)//当前结点为空时，返回上一层递归空间 
	{
		printf("#");
		return;
	}
	//结点非空时 
	visit(node);
	PreOrder(node->lchild);
	PreOrder(node->rchild);
}

1.2前序遍历—非递归

        简介：非递归，就是利用栈（就是一个存放树结点指针的数组，再加一个栈顶标记top），存放树节点的指针。树不为空的时候先入栈，随后，栈不为空时，再进行出栈操作。前序遍历出栈时，先出栈后，先访问该节点信息，随后再判断该节点是否有右孩子，有则，右孩子的指针存进栈中。再判断是否有左孩子，有则左孩子指针存进栈，

//前序遍历，非递归 
void Stack_PreOrder(BTNode *node)
{
	if(node==NULL)//树为空，不处理
	return;

    //创建一个栈，存放树结点类型的地址 
	BTNode* Stack[10];
	int top=-1;
	//工作指针，随着p指针，记录树的当前结点位置 
	BTNode *p=NULL;
	//当树非空时，进行操作 
	if(node !=NULL)
	{
		//入栈 
		top++;
		Stack[top]=node;
		
		//随后进行出栈操作，只有栈非空时，才可出栈 
		while(top != -1)
		{
			//取出此时栈顶元素 
			p=Stack[top];
			top--;
			//然后进行访问当前结点的相关操作 
			visit(p);
			//访问完根，在看该根的右孩子，入栈 ，因为是栈，先进后出，而前序为根左右，根出来后，右入栈，之后左入栈，最后出栈是栈顶出 
			if(p->rchild!=NULL)
			{
				top++;
				Stack[top]=p->rchild;
			}
			//访问完右孩子，在看该根的左孩子，入栈 
			if(p->lchild!=NULL)
			{
				top++;
				Stack[top]=p->lchild;
			}			
		}		
	}
}

二、中序遍历

2.1中序遍历—递归

        简介：左根右。不理解为啥的，可以画图，每进入一个新的函数，便是一个新的空间。

//中序遍历-递归 
void InOrder(BTNode *node)
{
	
	if(node==NULL)
	{
		printf("#");
		return;
	}
	InOrder(node->lchild);
	visit(node);
	InOrder(node->rchild);
}

2.2中序遍历—非递归

        简介：其实，栈也好，递归也罢，需要操作的，仅为两步，第一步为进入新树的一些列操作。操作完，进入第二步，进到另一方向孩子树中，该树中的操作，还是先进性第一步，再进行第二部，

        思想：中序遍历非递归操作，最外圈来个do-while循环，先执行，再判断。如果栈内非空，或者该结点不为空，都进行中序遍历操作。

        do-while里面的操作：先左子树操作：一直遍历，入栈元素，随后给指针地址换成该节点的左孩子，就是一直遍历到左孩子为空，才停止。至此，左根右中的左操作完毕。随后出栈元素，进行左根右中的根操作，访问根节点。至此，为第一步的操作。随后第二部，进入方向的树中，即结点指针换为右孩子地址，

//中序遍历-非递归
void StackInOrder(BTNode *node)
{
	if(node==NULL)//树为空，则不处理
	return;

    printf("中序遍历-非递归:");
	BTNode* p=node;
	BTNode* Stack[10];
	int top=-1;
	do
	{
		//当结点不为空时，入栈，并进入左孩子。 ——访问左孩子 
		while(p!=NULL)
		{
			top++;
			Stack[top]=p;
			p=p->lchild;
		}
		//一直遍历左，遍历到空，此时，出栈
		p=Stack[top];
		top--;
		
		visit(p);//访问根 
		p=p->rchild;//根访问完，随后，访问右孩子。随后，右孩子中，又是新的树，然后再进行左根右操作，形成循环，从上面再来一圈。 
		
	}while(top!=-1 || p!=NULL);//只要树不为空，或者栈内有元素，就一直进行操作。 
	
}

三、后序遍历

3.1后序遍历—递归

        简介：左右根。

// 后序遍历-递归
void PostOrder(BTNode *node)
{
	if(node==NULL)
	{
		printf("#");
		return;
	}
	PostOrder(node->lchild);
	PostOrder(node->rchild);
	visit(node);
}

3.2后序遍历—非递归

        简介：这个比较麻烦，不过还是利用描边法去做，根据描边法，根节点被访问两次，第一次时入栈时，第二次时判断是否出栈时，就看从那一层返回到根节点的，如果从右孩子返回的，则进行出栈操作，先记录当前结点，再出栈。否则，则进行右子树结点的出栈，

        这里面，跟中序，略有不同，入栈和出栈的情况需要判断，所以需要用栈顶指针时刻对比。

先跟根结点入栈，随后当栈内不为空时，一直进行遍历操作。先进性第一步的入栈操作（当上层遍历，即不是栈顶指针的左孩子又不是右孩子时，更新工作指针为左孩子，随后进行一直左孩子入栈操作）第二步，左孩子到底了，此时需要面临出栈，因此给当前栈顶元素取出来，如果该树没有左孩子，或者pre与右孩子地址相同，则进行出栈操作，并记录出栈前的指针p，否则则给右孩子入栈。

void StackPostOrder(BTNode *node)
{
	printf("后序遍历-非递归：");
	if(node==NULL)
	return; 
	
	BTNode *p=node;//工作指针 
	BTNode *pre=NULL;//表示上层结点位置 
	//栈 
	BTNode *Stack[10];
	int top=-1;
	//先跟根节点入栈，为了方便第一次判断
	top++;
	Stack[top]=p;
	 
	do
	{
		//先判断上层结点是否遍历过，没有，则进行左子树都入栈，入到底
		if(pre!=Stack[top]->lchild && pre!=Stack[top]->rchild)
		{
			p=Stack[top]->lchild;//上次没有遍历过左右孩子，那么开始栈顶元素的左孩子入栈操作。
			while(p!=NULL)
			{
				top++;
				Stack[top]=p;
				p=p->lchild;	
			}	
		}
		//左孩子方向弄到底后，开始判断，是否需要出栈输出。
		p=Stack[top];//记录此时的栈顶元素
		if(p->rchild==NULL || pre==p->rchild)//如果右孩子为空，或者上一层和当前结点的右孩子相等，则输出 
		{
			pre=p;//记录当前结点地址 
			visit(p);//输出 
			top--;//输出了，栈内指针减少 
		}
		else
		{
			top++;
			Stack[top]=p->rchild;//右孩子入栈	
		} 
		
		
	}while(top!=-1); 
}

   五、总代码

5.1代码

#include <stdio.h>
#include <stdlib.h>
//创建树,孩子链表 
typedef struct BTNode
{
	int data;
	struct BTNode *rchild,*lchild;
	
}BTNode; 
//创建树结点，并初始化
BTNode* BuyNode(int x)
{
	BTNode* node=(BTNode*)malloc(sizeof(BTNode));
	node->data=x;
	node->lchild=NULL;
	node->rchild=NULL;
	
	return node;	
} 
//手动创建树
BTNode* CreatTree()
{
	BTNode* node1=BuyNode(1);
	BTNode* node2=BuyNode(2);
	BTNode* node3=BuyNode(3);
	BTNode* node4=BuyNode(4);
	BTNode* node5=BuyNode(5);
	
	node1->lchild=node2;
	node1->rchild=node3;
	node2->lchild=node4;
	node2->rchild=node5;
	return node1;		
} 
//访问当前结点时的操作 
void visit(BTNode *node)
{
	printf("%d",node->data);	
} 
//前序遍历，递归 
void PreOrder(BTNode *node)
{
	if(node==NULL)//当前结点为空时，返回上一层递归空间 
	{
		printf("#");
		return;
	}
	//结点非空时 
	visit(node);
	PreOrder(node->lchild);
	PreOrder(node->rchild);
}
//前序遍历，非递归 
void Stack_PreOrder(BTNode *node)
{
	if(node==NULL)
	return;
	
	printf("前序遍历-非递归：");
	//创建一个栈，存放树结点类型的地址 
	BTNode* Stack[10];
	int top=-1;
	//工作指针，随着p指针，记录树的当前结点位置 
	BTNode *p=NULL;
	//当树非空时，进行操作 
	if(node !=NULL)
	{
		//入栈 
		top++;
		Stack[top]=node;
		
		//随后进行出栈操作，只有栈非空时，才可出栈 
		while(top != -1)
		{
			//取出此时栈顶元素 
			p=Stack[top];
			top--;
			//然后进行访问当前结点的相关操作 
			visit(p);
			//访问完根，在看该根的右孩子，入栈 ，因为是栈，先进后出，而前序为根左右，根出来后，右入栈，之后左入栈，最后出栈是栈顶出 
			if(p->rchild!=NULL)
			{
				top++;
				Stack[top]=p->rchild;
			}
			//访问完右孩子，在看该根的左孩子，入栈 
			if(p->lchild!=NULL)
			{
				top++;
				Stack[top]=p->lchild;
			}			
		}		
	}
}
//中序遍历-递归 
void InOrder(BTNode *node)
{
	
	if(node==NULL)
	{
		printf("#");
		return;
	}
	InOrder(node->lchild);
	visit(node);
	InOrder(node->rchild);
}
//中序遍历-非递归
void StackInOrder(BTNode *node)
{
	if(node==NULL)
	return;
	
	printf("中序遍历-非递归:");
	BTNode* p=node;
	BTNode* Stack[10];
	int top=-1;
	do
	{
		//当结点不为空时，入栈，并进入左孩子。 ——访问左孩子 
		while(p!=NULL)
		{
			top++;
			Stack[top]=p;
			p=p->lchild;
		}
		//一直遍历左，遍历到空，此时，出栈
		p=Stack[top];
		top--;
		
		visit(p);//访问根 
		p=p->rchild;//根访问完，随后，访问右孩子。随后，右孩子中，又是新的树，然后再进行左根右操作，形成循环，从上面再来一圈。 
		
	}while(top!=-1 || p!=NULL);//只要树不为空，或者栈内有元素，就一直进行操作。 
	
}
// 后序遍历-递归
void PostOrder(BTNode *node)
{
	if(node==NULL)
	{
		printf("#");
		return;
	}
	PostOrder(node->lchild);
	PostOrder(node->rchild);
	visit(node);
}
//后序遍历-非递归
void StackPostOrder(BTNode *node)
{
	printf("后序遍历-非递归：");
	if(node==NULL)
	return; 
	
	BTNode *p=node;//工作指针 
	BTNode *pre=NULL;//表示上层结点位置 
	//栈 
	BTNode *Stack[10];
	int top=-1;
	//先跟根节点入栈，为了方便第一次判断
	top++;
	Stack[top]=p;
	 
	do
	{
		//先判断上层结点是否遍历过，没有，则进行左子树都入栈，入到底
		if(pre!=Stack[top]->lchild && pre!=Stack[top]->rchild)
		{
			p=Stack[top]->lchild;//上次没有遍历过左右孩子，那么开始栈顶元素的左孩子入栈操作。
			while(p!=NULL)
			{
				top++;
				Stack[top]=p;
				p=p->lchild;	
			}	
		}
		//左孩子方向弄到底后，开始判断，是否需要出栈输出。
		p=Stack[top];//记录此时的栈顶元素
		if(p->rchild==NULL || pre==p->rchild)//如果右孩子为空，或者上一层和当前结点的右孩子相等，则输出 
		{
			pre=p;//记录当前结点地址 
			visit(p);//输出 
			top--;//输出了，栈内指针减少 
		}
		else
		{
			top++;
			Stack[top]=p->rchild;//右孩子入栈	
		} 
		
		
	}while(top!=-1); 
}
int main()
{
	BTNode* root=CreatTree();
	//前序遍历打印
	printf("前序遍历-递归："); 
	PreOrder(root);//递归 
	printf("\n"); 
	Stack_PreOrder(root);//非递归，栈来做 
	printf("\n"); 
	printf("中序遍历-递归：");
	InOrder(root); 
	printf("\n"); 
	StackInOrder(root); 
	printf("\n"); 
	printf("后续遍历-递归：");
	PostOrder(root);
	printf("\n"); 
	StackPostOrder(root);
	return 0;
 }

5.2运行结果图

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/955630.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

plsql ebs 工作中的简单笔记

plsql ebs 工作中的简单笔记

工作流中给系统界面发送消息&#xff1a; PROCEDURE wf_notify(p_sender IN VARCHAR2 DEFAULT SYSADMIN,p_receiver IN VARCHAR2,p_subject IN VARCHAR2,p_content_text IN VARCHAR2);PROCEDURE wf_notify(p_sender IN VARCHAR2 DEFAULT SYSADMIN,---发送…
阅读更多...
模块和包（Python语言）

模块和包（Python语言）

目录 一、什么是模块&#xff1f; 二、模块导入方式 2.1方法一&#xff1a; 2.2方法二&#xff1a; 2.3模块导入搜索路径&#xff1a; 2.4模块调用格式&#xff1a; 三、OS模块操作文件 四、模块的操作 4.1模块作用&#xff1a; 4.2模块分类&#xff1a; 4.3魔术变量…
阅读更多...
EXSI技术--Exsi资源分割

EXSI技术--Exsi资源分割

我们在搭建好环境之后，就类似于有了一个服务器，现在我们就可以对着一个服务器进行一个虚拟化的操作。给不同的用户使用操作。现在，有一个名叫mit的科技企业需要租用服务器用于创建MySQL数据库集群；另外还有一个IECQ的企业需要服务器搭建电商平台。下面我们为这两个企业分割…
阅读更多...
进程Start

进程Start

Linux中的命令解释器和Windows的程序管理器explorer.exe一样地位,都是在用户态下运行的进程 共享变量发生不同进程间的指令交错&#xff0c;就可能会数据出错 进程只作为除CPU之外系统资源的分配单位 CPU的分配单位是线程 每个进程都有自己的独立用户空间 内核空间是OS内核的…
阅读更多...
提高工作效率的一键查询和保存大量快递物流信息的技巧

提高工作效率的一键查询和保存大量快递物流信息的技巧

在如今快速发展的电商行业中&#xff0c;物流服务的准确与便捷是保证顺利交付商品的重要环节。为了方便用户追踪物流&#xff0c;固乔快递查询助手应运而生。这款软件不仅能够快速查询快递单号的物流信息&#xff0c;还具备保存查询结果的功能&#xff0c;方便用户随时查看。 首…
阅读更多...
光伏电站、变电站、等直流系统电参量测量仪器怎么选型

光伏电站、变电站、等直流系统电参量测量仪器怎么选型

安科瑞虞佳豪 壹捌柒陆壹伍玖玖零玖叁 应用场景 工作拓扑图 功能 ①对电能参数进行采样计量和监测&#xff0c;逆变器或者能量管理系统&#xff08;EMS&#xff09;与之进行通讯&#xff0c;根据实时功率及累计电能实现防逆流、调节发电量、电池充放电等功能&#xff1b; ②…
阅读更多...
初始化列表

初始化列表

文章目录 一. 初始化列表是什么&#xff1f;二. 为什么要有初始化列表&#xff1f;三. 初始化列表的特性四. explicit关键字五. statis成员六. 友元七. 内部类八. 匿名对象九. 编译器优化总结&#xff1a; 一. 初始化列表是什么&#xff1f; 初始化列表是构造函数真正初始化的地…
阅读更多...
基于stm32的烟雾浓度检测报警proteus仿真设计(仿真+程序+讲解）

基于stm32的烟雾浓度检测报警proteus仿真设计(仿真+程序+讲解）

基于STM32的烟雾浓度检测报警仿真设计(仿真程序讲解&#xff09; 1.主要功能2.仿真3. 程序4. 资料清单&下载链接 基于STM32的烟雾浓度检测报警仿真设计(仿真程序讲解&#xff09; 仿真图proteus 8.9 程序编译器&#xff1a;keil 5 编程语言&#xff1a;C语言 设计编号&a…
阅读更多...
Python编程

Python编程

Lesson I 解rar压缩包的密码 1 下载Python并安装 网址: 注意选对是32 bit还是64 bit Python Releases for Windows | Python.orgThe official home of the Python Programming Languagehttps://www.python.org/downloads/windows/ 2 安装unrar pip install unrar 3 下载u…
阅读更多...
JS中方法、函数、属性是一个东西吗

JS中方法、函数、属性是一个东西吗

在 JavaScript 中&#xff0c;方法、函数和属性是相关但不完全相同的概念。 方法&#xff08;Method&#xff09;&#xff1a;在对象中&#xff0c;方法是对象的属性&#xff0c;但它的值是一个函数。方法可以通过对象来调用&#xff0c;并且可以访问对象的属性和其他方法。 …
阅读更多...
从《离婚律师》中学习代理模式

从《离婚律师》中学习代理模式

〇、前言 在2014年的时候&#xff0c;有一部非常火爆的电视剧叫做《离婚律师》&#xff0c;里面讲述了两名离婚律师池海东和罗郦的爱恨情仇&#xff0c;片子非常好看&#xff0c;当时我自己也怒刷了好几遍。 那么&#xff0c;在本剧的第四集中&#xff0c;有一段非常搞笑的剧情…
阅读更多...
Linux学习之逻辑卷LVM用途和创建

Linux学习之逻辑卷LVM用途和创建

理论基础 Linux文件系统建立在逻辑卷上&#xff0c;逻辑卷建立在物理卷上。 物理卷处于LVM中的最底层&#xff0c;可以将其理解为物理硬盘、硬盘分区或者RAID磁盘阵列&#xff0c;这都可以。卷组建立在物理卷之上&#xff0c;一个卷组可以包含多个物理卷&#xff0c;而且在卷组…
阅读更多...
新手小白如何租用GPU云服务器跑深度学习

新手小白如何租用GPU云服务器跑深度学习

最近刚学深度学习&#xff0c;自己电脑的cpu版本的pytorch最多跑个LexNet&#xff0c;AlexNet直接就跑不动了&#xff0c;但是作业不能不写&#xff0c;实验不能不做。无奈之下&#xff0c;上网发现还可以租服务器这种操作&#xff0c;我租的服务器每小时0.78人民币&#xff0c…
阅读更多...
Linux驱动——Tiny4412芯片_Source Insight的下载+Linux3.5内核下工程的创建

Linux驱动——Tiny4412芯片_Source Insight的下载+Linux3.5内核下工程的创建

文章目录 前言Source Insight的下载1.下载地址2.下载步骤 linux3.5内核下工程的创建 前言 本博客仅作为笔记总结&#xff0c;以及帮助有需要的人&#xff0c;不作权威解释。 Source Insight的下载 1.下载地址 官网&#xff1a;https://www.sourceinsight.com/ 另外可以选择…
阅读更多...
【计算机网络】一文带你弄懂DNS解析过程（最强详解！！）

【计算机网络】一文带你弄懂DNS解析过程（最强详解！！）

目录 首先了解一下什么是DNS协议吧 域名的结构 顶级域名 二级域名 根域名 DNS的查询方式 递归查询 迭代查询 完整域名解析系统 首先了解一下什么是DNS协议吧 DNS&#xff08;Domain Name System&#xff09;是一个用于将域名&#xff08;例如www.example.com&#xff09;…
阅读更多...
BTC价格预测：灰度突如其来的胜利是否会打破“九月魔咒”？

BTC价格预测：灰度突如其来的胜利是否会打破“九月魔咒”？

加密市场即将进入第三季度交易的最后阶段&#xff0c;由于9月份被视为是比特币的下跌时期&#xff0c;大多数投资者都预测加密货币之王将会进一步下跌。然而&#xff0c;事情却发生了逆转&#xff0c;灰度突如其来的胜利是否会打破“九月魔咒”&#xff1f; 受该事件影响&#…
阅读更多...
15.坐标添加带箭头的线

15.坐标添加带箭头的线

ol的官网示例中有绘制带箭头的线的demo&#xff0c;那个是交互式绘制&#xff0c;而不是根据经纬度坐标添加&#xff0c;在其基础上稍作修改&#xff0c;即可转为通过经纬度添加带箭头的线的功能&#xff0c;线和箭头的粗细大小样式都可以自定义 代码如下 <!DOCTYPE HTML P…
阅读更多...
【工程实践】使用git clone 批量下载huggingface模型文件

【工程实践】使用git clone 批量下载huggingface模型文件

前言 经常需要下载模型到服务器&#xff0c;使用git clone方法可以快速实现模型下载。 1.选定要下载的模型 以下载moka-ai/m3e-base为例&#xff0c;切换到Files and versions。 2.更改下载网页的url 如上图所示&#xff0c;当前要下载模型网页的url为&#xff1a; https://hu…
阅读更多...
【C++初阶】反向迭代器的实现

【C++初阶】反向迭代器的实现

&#x1f466;个人主页&#xff1a;Weraphael ✍&#x1f3fb;作者简介&#xff1a;目前学习C和算法 ✈️专栏&#xff1a;C航路 &#x1f40b; 希望大家多多支持&#xff0c;咱一起进步&#xff01;&#x1f601; 如果文章对你有帮助的话 欢迎 评论&#x1f4ac; 点赞&#x1…
阅读更多...
【高阶产品策略】策略价值量化之数据指标

【高阶产品策略】策略价值量化之数据指标

文章目录 1、数据指标概述2、通用指标3、WEB端常用指标4、移动端常用指标5、如何选择一个合适的数据指标 1、数据指标概述 2、通用指标 3、WEB端常用指标 4、移动端常用指标 5、如何选择一个合适的数据指标
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023