⛄一、PM模型图像降噪简介
为了提高去除噪声和保留细节信息的算法的性能,Peroha等提出以热学中扩散方程式为基础的扩散算法即为PM模型。该模型主要是在经典各向异性扩散方dgi,j,t/dt=div(d∇g)上提出将其中的扩散系数d用函数控制的扩散系数替代。PM模型为
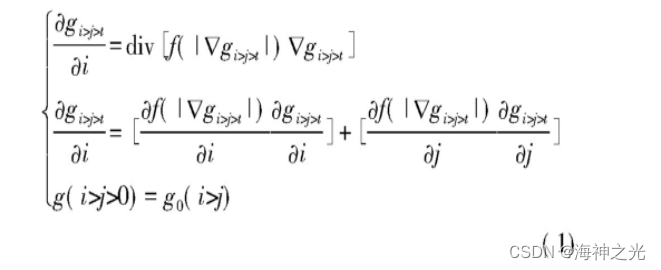
其中,f(|∇gi,j,t|)是一个扩散系数函数,∇是梯度,div是散度,g0(i,j)是一个最开始的像素点,(i,j)是图像中像素点位置,t为时间间隔。在传统的PM模型中,Perona和MAlik提出了两个满足以下条件的函数f(|∇gi,j,t|):
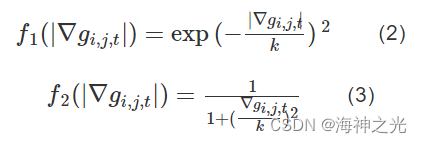
扩散系数函数f(|∇gi,j,t|)应具有以下特点:
(1)函数f(|∇gi,j,t|)是以|∇gi,j,t|为变量,随着变量上升而下降;
(2)当|∇gi,j,t|→0时,f(|∇gi,j,t|)=1;
(3)当|∇gi,j,t|→1时,f(|∇gi,j,t|)=0.
常量k为梯度门限,判断k与|∇gi,j,t|大小关系,主要用于判断是否对图像中某个范围进行扩散。将式(1)离散化,得
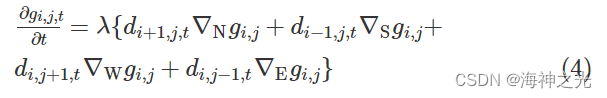
式(4)中di+1,j,t,di-1,j,t,di,j+1,t,di,j-1,t分别是北,南,西,东上的扩散系数值,且∇Ngi,j,∇Sgi,j,∇Wgi,j,∇Egi,j分别表示北,南,西,东方向上的梯度值,λ是衡量扩散速度的常量。则处理后新的像素值fi,j为
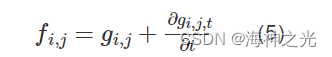
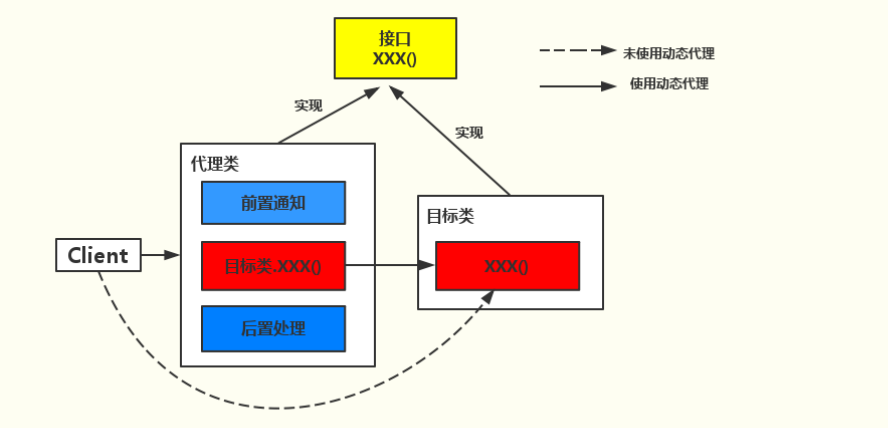
综上分析可得PM扩散模型如图1所示。
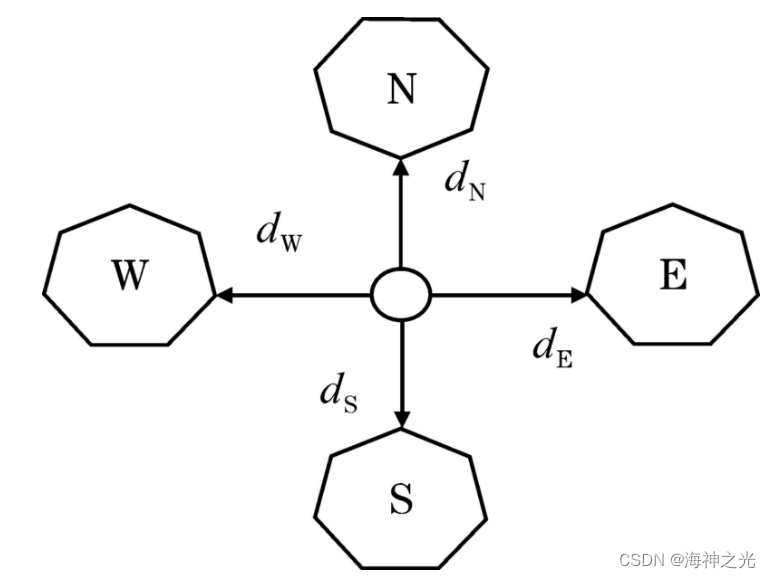
图1 传统PM扩散模型
传统PM模型仍有不足之处,对于有些边缘化的噪声点去噪效果不甚理想;在该模型中,扩散函数不利于图像的平滑,另外只选择了4个方向的扩散,易造成图像内容信息损失,出现模糊现象。
⛄二、部分源代码
clear all;
close all;
%Io=imread(‘Image/Article3.bmp’);% 读入一幅图像
%Io=imread(‘Image/GZC01.bmp’);
Io=imread(‘pepper.bmp’);
%Io=imread(‘Image/cameraman.bmp’);
I=double(rgb2gray(Io));
In=I;
% I=double(Io);
% stan_var=20;
% var=stan_var^(2);
% IN1=randn(size(I))*stan_var;
% In=I+IN1;
% save(‘In’);
% % load(‘In’);
figure(2),imshow(In,[],‘Border’,‘tight’);
figure(3),imshow(I,[],‘Border’,‘tight’);
lamda=0.2;
iter=350;
K=2.5;
[ImMAE,PSNRAll,Is]=diffusion_PM(I,In,iter,lamda,K);
figure(4),imshow(Is,[],‘Border’,‘tight’);
figure(5),imshow(Is-In,[],‘Border’,‘tight’);
[Ny,Nx]=size(Is);
x=1:Nx;
level=fix(Ny/2);
y=Is(level,:);
y1=I(level,:);
y2=In(level,:);
figure(14);
subplot(2,1,1); plot(x,y,x,y1);
title(‘SmoothImage And OriginalImage’)
subplot(2,1,2); plot(x,y,x,y1,x,y2);
title(‘NoiseImage And OriginalImage’)
figure(6);
x=1:iter;
plot(x,PSNRAll);title(‘PSNR’)
figure(7);
x=1:iter;
plot(x,ImMAE);title(‘MAE’)
⛄三、运行结果







⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]晏满钰,文成玉.改进的PM模型的医学超声图像去噪算法[J].成都信息工程大学学报. 2019,34(06)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除