Problem - E - Codeforces

题意：

 

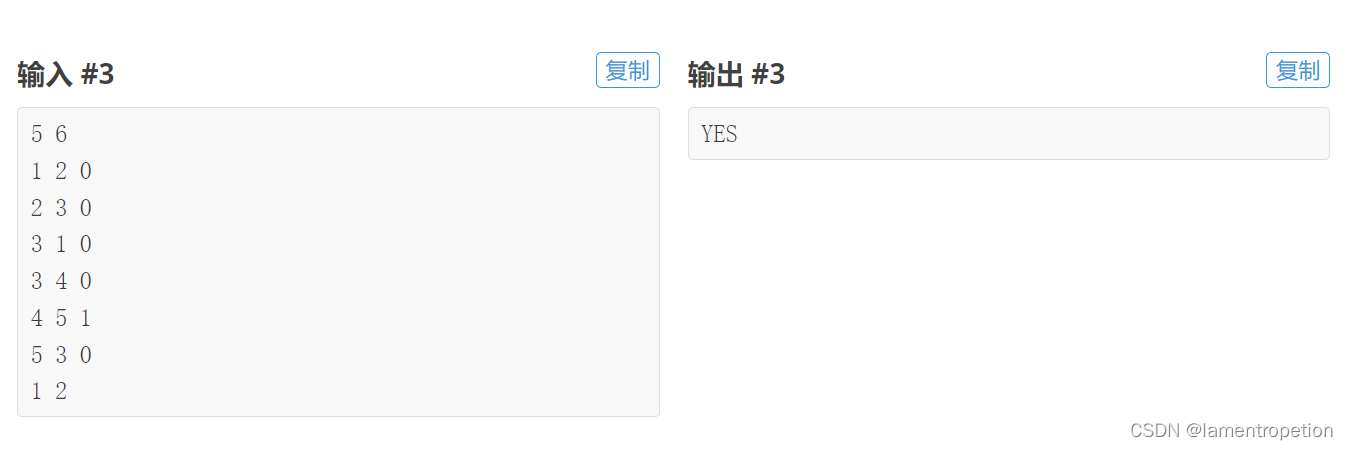
思路：

st 到 ed存在多条路径

注意到在同一个边双连通分量中，如果存在一条边的边权是1，那么这个边双连通分量中所有点对的路径中都存在一条边的边权是1，因此我们考虑缩点，缩完点之后是一棵树，这样路径就唯一了。只需要看 st的分量 到 ed的分量 的路径中是否存在边权是1的边即可

Code：

#include <bits/stdc++.h>

#define int long long
#define lowbit(x) (x & (-x))

using i64 = long long;

constexpr int N = 2e6 + 10;
constexpr int M = 2e6 + 10;
constexpr int P = 2e6;
constexpr i64 Inf = 1e18;
constexpr int mod = 1e9 + 7;
constexpr double eps = 1e-6;

std::stack<int> S;
std::vector<std::array<int,3> > E(M);
std::vector<std::array<int, 2> > adj[N], adj2[N];

bool ok = false;
int n, m, u, v, w, st, ed;
int tot = 0, cnt = 0;
int dfn[N], low[N], vis[N], bl[N], vis2[N], can[N];

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++tot;
    S.push(u);
    vis[u] = 1;
    for (auto [v, w] : adj[u]) {
        if (v == fa) continue;
        if (!dfn[v]) {
            tarjan(v, u);
            low[u] = std::min(low[u], low[v]);
        }else if (vis[v]) low[u] = std::min(low[u], low[v]);
    }

    if (dfn[u] == low[u]) {
        bl[u] = ++cnt;
        while(S.top() != u) {
            bl[S.top()] = cnt;
            vis[S.top()] = 0;
            S.pop();
        }
        S.pop();
        vis[u] = 0;
    }
}
void dfs(int u, int fa, int f) {
    if (can[u]) f = 1;
    if (u == bl[ed]) {
        if (f == 1) ok = true;
    }
    for (auto [v, w] : adj2[u]) {
        if (v == fa) continue;
        if (!vis2[v]) {
            vis2[v] = 1;
            dfs(v, u, f | w);
            vis2[v] = 0;
        }
    }
}
void solve() {
    std::cin >> n >> m;
    for (int i = 1; i <= m; i ++) {
        std::cin >> u >> v >> w;
        adj[u].push_back({v, w});
        adj[v].push_back({u, w});
        E[i] = {u, v, w};
    }

    tarjan(1, 0);
    for (int i = 1; i <= m; i ++) {
        if (bl[E[i][0]] == bl[E[i][1]] && E[i][2]) {
            can[bl[E[i][0]]] = 1;
        }
    }

    for (int i = 1; i <= m; i ++) {
        if ((bl[E[i][0]] != bl[E[i][1]])) {
            adj2[bl[E[i][0]]].push_back({bl[E[i][1]], E[i][2]});
            adj2[bl[E[i][1]]].push_back({bl[E[i][0]], E[i][2]});
        }
    }

    std::cin >> st >> ed;
    st = bl[st];
    dfs(st, 0, 0);
    if (ok == true) {
        std::cout << "YES" << "\n";
    }else {
        std::cout << "NO" << "\n";
    }
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t = 1;

    while (t--) {
        solve();
    }
    
    return 0;
}