首先左旋和右旋的概念都是在平衡二叉树的基础上提出的。并对AVL树 SB树 红黑树在原理层面进行了简单的介绍，无coding。

什么是左旋？

假设存在下述平衡二叉树（某个结点的左子节点都小于该结点，右子结点右大于大结点），如果要进行左旋，则将整个数往左旋转，C成为新的头节点。

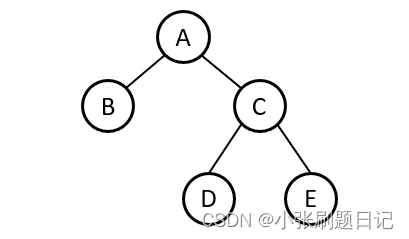
 因为原树为平衡二叉树，那么C的左子树都小于C，并且都大于A，那么C成为新的头节点过后将C的左子树挂在A的右方即可，如下图所示：

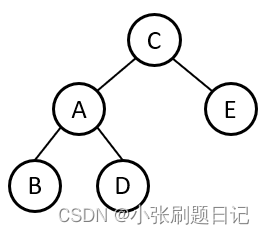
什么是右旋？

和左旋对应，如下图所示的树：

 

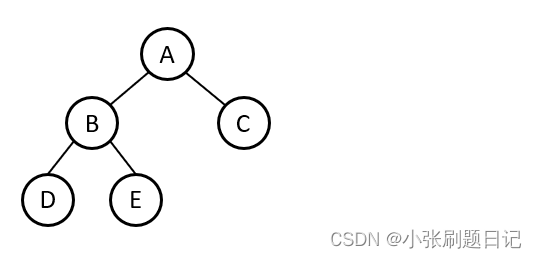
 右旋过后图为：

 

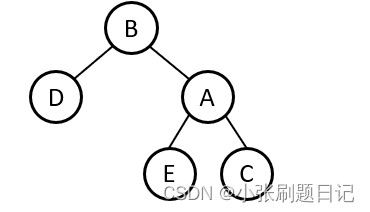
AVL树对于四种情况怎么进行调整（AVL树需要更新高度信息）：

1. LL 左树左边过长

做一次右旋即可，比如：

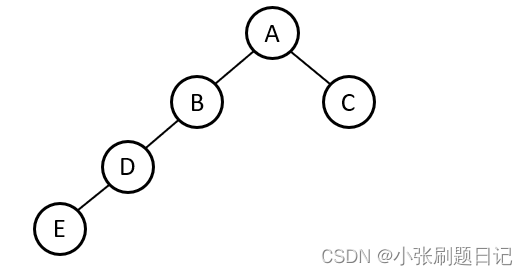
右旋后：

 

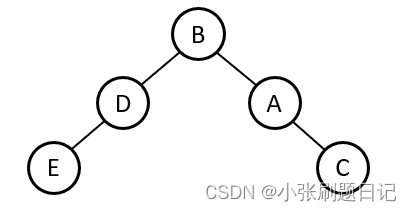
2. RR 右树右边过长

做一次左旋，具体的图就不贴了，根据左旋右旋的概念对应LL类型进行理解即可。

3. LR 左树右边过长

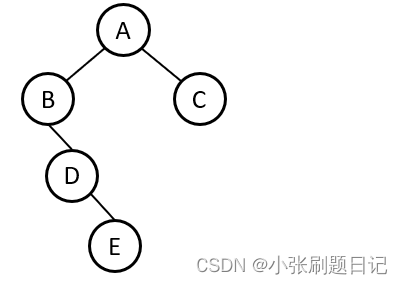
这个时候需要将左树的右子树头节点调整为头部，及将D调整为头节点，需要进行一次左旋和一次右旋，如下图所示：

4. RL 右树左边过长

需要将右树的左子树头节点调整为头部做，一次右旋和左旋，具体的图就不贴了，根据左旋右旋的概念对应LR类型进行理解即可。

Size-Balance 树 即-SB树：

树的构造原理为：叔叔树的大小不能小于其任何侄子数的大小，也就是说，如下图所示，A C代表的是节点，B D E都代表子树，B的大小不能够小于D E中任何一个子树的大小。

调整方式：

1. LL 左子树的左子树大于右子树 

右旋 ； 递归调整（对任何子结点发生变化的结点进行LL同样的操作）。

2. RR 右子树的右子树大于左子树 

左旋 ； 递归调整（对任何子结点发生变化的结点进行RR同样的操作）。

3. LR 左子树的右子树大于左子树

让左子树的右子树头节点，通过先左旋再右旋成为整个树的头节点 ； 递归调整。

3. RL 右子树的左子树大于右子树

让右子树的左子树头节点，通过先右旋再左旋成为整个树的头节点 ； 递归调整。.

红黑树：

1. 每个结点不是红就是黑

2. 头节点和底层叶节点（为空的点）必须为黑

3. 任何两个红节点不能相邻

4. 对于任何一个子树来说，头节点出发到叶节点要求黑节点一样。

具体的调整方式有些复杂，这里不做过多介绍，可以移步：

红黑树详解_晓之木初的博客-CSDN博客_红黑树https://blog.csdn.net/u014454538/article/details/120120216