逻辑智能体

• 逻辑智能体：基于知识的智能体
• 知识和推理的重要性
  • 部分可观察的环境
  • 自然语言理解
  • 基于知识的智能体的灵活性

Knowledge bases

• 知识库是一组用形式化语言表述的陈述句，其中包含有系统需要了解的信息。
• 在构建一个智能体时，通常采用“告诉”和“询问”的方式，即先将需要的知识加入知识库中，然后智能体会通过查询知识库中的信息来得出答案。
• 智能体可以从知识层次上进行观察，即从它们所知道的知识来描述，而不考虑具体的实现细节。
• 也可以从实现层次上进行观察，即从知识库的数据结构和处理这些数据结构的算法来描述。通过这种方式，智能体能够有效地利用知识库中的信息进行推理和决策。

一个简单的基于知识的智能体

如下是基于知识的Agent的程序轮廓。与其他Agent一样，基于知识的Agent用感知信息作为输入，返回一个行动。Agent维护一个知识库，KB，该知识库在初始化时就包含了一些背景知识。

• 一个智能体（agent）必须具备的几个关键能力。
  1. 智能体需要能够表示状态和行为，以便在环境中执行任务。
  2. 此外，智能体需要能够将新的感知信息纳入到其内部状态中，并更新其对世界的状态表示。
  3. 智能体还需要能够推导关于世界的隐藏属性，并基于这些推断出合适的行为。
  4. 这些能力可以通过代表性方法来实现，从而使智能体能够在环境中自主地执行任务。

一般逻辑

• 逻辑是一种用于表示信息以推断出结论的形式语言。
• 语法定义了该语言中的句子，即如何构建语句的规则。
• 而语义定义了句子的“含义”，即句子在世界中的真实性。
• 例如，算术语言中的x+2≥y是一个句子，而x2+y>不是一个句子。
• x+2≥y是真的，如果x+2的数值不小于y的数值。在x=7，y=1的世界中x+2≥y是真的，在x=0，y=6的世界中x+2≥y是假的。
• 这些知识与逻辑学中语法和语义的基本概念相关。同时，这些概念在人工智能中也具有重要作用，尤其是在推理和决策系统中。

Entailment 蕴涵

• 逻辑中的关键概念之一是蕴涵，它指的是两个命题之间的关系，其中一个命题逻辑上可以推导出另一个命题。也就是说，如果命题A蕴涵命题B，则如果A为真，B也必须为真。例如，命题“所有人都会死亡”蕴涵命题“苏格拉底会死亡”，因为苏格拉底是一个人。

• 蕴涵表示一个语句逻辑上跟随另一个语句而出现，即如果一个语句A蕴涵另一个语句B，那么当A为真时，B也必须为真。

• 这种蕴涵关系可以用$KB |= α $来表示，其中KB是一个知识库，sentence α是一个语句。

• 如果在KB为真的所有世界中， α也为真，则KB蕴涵 α。

• 蕴涵是基于语义的关系，因为它基于语句在不同世界中的真值。因此，语句的语法语义是蕴涵关系的基础。

• 如一个知识库包含“巨人队赢了”和“红队赢了”蕴涵“要么巨人队赢了，要么红队赢了”，以及x + y = 4蕴涵4 = x + y。

Models模型

当需要精确描述时，用术语模型取代“可能世界"

• 首先，当一个语句 $\alpha$ 在一个模型 $m$ 中为真时，我们称 $m$ 是 $\alpha$ 的一个模型。用语言表达就是“$m$ 是 $\alpha$ 的一个模型”表示语句 $\alpha$ 在模型 $m$ 中为真。
• 其次，$M(\alpha )$ 表示 $\alpha$ 的所有模型的集合。
• 最后，当且仅当在知识库 KB 为真的所有模型中 $\alpha$ 为真时，我们说 $\alpha$ 在 KB 中是可满足的。用语言表达就是“在 KB 为真的所有模型中 $\alpha$ 为真”等价于“KB |= $\alpha$”。
• 例如，当知识库 KB 包含“Giants 赢了”和“Reds 赢了”时，语句 $\alpha$ = “Giants 赢了”在 KB 中是可满足的。

蕴涵与推理

命题逻辑

逻辑连接词

两个句子在逻辑上是等价的(逻辑等价）：

枚举推理

所有模型的深度优先枚举是合理和完整的

**但是，对于n个符号，时间复杂度为$O(2^n)$，空间复杂度为$O(n)$；问题是co-NP-complete的**

有效性

可满足性

推导和证明

• 证明方法主要有两类：推理规则的应用和模型检查。
  1. 其中推理规则的应用是通过合法的（sound）推理规则，从已知的句子中产生新的句子，通过应用一系列推理规则来构建证明。这个过程可以看作是在搜索空间中使用推理规则作为操作符的搜索过程。通常需要将句子转换成正常形式，以便应用推理规则。
  2. 另一种方法是模型检查，即对于给定的句子，通过枚举其所有可能的赋值，检查是否存在一个模型使得该句子为真。这种方法包括真值表枚举（在 n 中始终是指数级别的），改进的回溯算法（如Davis-Putnam-Logemann-Loveland算法）和模型空间中的启发式搜索（sound但不完备）。

霍恩子句

Forward chaining 前向链接

前向链接算法：

流程：
箭头表示决定某个符号的符号，比如，A和B蕴涵L，

1. agenda为AB，count如图所示
   
2. 处理完A，对应的count-1
   
3. AB都为真且处理完毕，此时知道L为真，待处理
   
4. 此时M计数为0，添加到agenda待处理
   
5. 处理完毕后P再次变为0
   
6. 最后处理Q
   
7. 前向链接算法结束“：
   

• 对于霍恩子句构成的知识库，Forward chaining 是
  1. 可靠的：每个推理本质上是分离规则的一个应用
  2. 完备的：每个被蕴涵的原子语句都将得以生成

Proof of completeness（完备性）

)

Backward chaining 反向链接

1. 从目标Q开始
   
2. 试图找到能令蕴涵式P->Q为真的情况
   
3. 同理继续往回推，几个步骤后得到这样的情况：根据AB得到L为真
   
4. 根据BL得到M为真
   
5. 最后结果是相同的：
   

Resolution归结

合取范式（CNF）

合取范式（CNF）是一个逻辑学术语，它表示为文字的析取式的合取式，其中每个文字都是一个变量或者它的否定形式，而每个合取项都是由一个或多个文字的析取组成的，这些合取项被称为clauses。因此，CNF是由多个clause（子句）组成的合取式。
例如：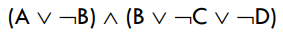

Resolution inference rule归结推理规则 (for CNF):

其中li和mj是互补的文字，例如：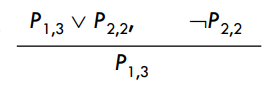

• 命题逻辑中归结是可靠和完备的

CNF转换

举例

小结

• 逻辑智能体应用推理于知识库，以推导新信息并作出决策。逻辑的基本概念包括：
  1. 语法：句子的形式结构
  2. 语义：句子关于模型的真假性
  3. 蕴涵：给定一个句子，另一个句子成立的必要条件
  4. 推理：从其他句子推导出新句子
  5. 可靠性：推导过程只产生蕴涵的句子
  6. 完备性：推导可以产生所有蕴涵的句子
• “Wumpus world”需要能够表示部分和否定信息，通过情况进行推理等能力。
• 前向链接和后向链接是线性时间的，并且对于霍恩子句具有完备性。
• 归结对于命题逻辑具有完备性。
• 命题逻辑缺乏表达能力。