目录
15.1 基本概念
概率模型
生成模型与判别模型
概率图模型
马尔可夫链,马尔可夫随机场和 CRF
15.2 数学中的HMM
HMM的两个基本假设
15.3 HMM的三个基本问题
概率计算问题
预测问题
学习问题
15.4 HMM3个基本问题的计算
概率计算问题
预测问题
学习问题
15.6 HMM实例
15.1 基本概念
概率模型
所谓概率模型(probabilistic model),顾名思义,就是将学习任务归结于计算变量概率分布的模型。
概率模型非常重要。在生活中,我们经常需要根据一些已经观察到的现象来推测和估计未知的东西,这种需求恰恰是概率模型的推断(inference)行为所做的事情。
推断的本质是:利用可观测的变量,推测未知变量的条件分布。
本章要讲HMM 和下一章的CRF都是概率模型,之前讲过的朴素贝叶斯和逻辑回归也是概率模型
生成模型与判别模型
概率模型又可以分为两类:生成模型(generative mo odel)和判别模型(discriminative model)。既然概率模型可以通过可观测变量推断部分未知变量,那么我们将可观测变量的集合命名为O,将我们感兴趣的未知变量的集合命名为Y。
生成模型学习后得到的是O与Y的联合概率分布P(OY),而判别模型学习后得到的是条件概率分布P(Y|O)
之前我们学过的朴素贝叶斯模型是生成模型,而逻辑回归是判别模型。
对于某一个给定的观察值O,运用条件概率P(Y|O)很容易求出它对于不同Y的取值。
那么当遇到分类问题时,直接就可以运用判别模型,判断给定O对于哪一个Y值的条件概率最大,从而来判断该观测样本属于的类别。
使用生成模型直接给观测样本分类有点困难,但也不是不可行,可以运用贝叶斯法则,将生成模型转化为判别模型,但是这样显然比较麻烦。
在分类问题上,判别模型一般更具优势。不过生成模型自有其专门的用途,HMM就是一种生成模型
概率图模型
概率图模型(probabilistic graphical model)是一种以图(graph)为表示工具来表达变量间相关关系的概率模型。
这里说的图就是数据结构中图的概念:一种由节点和连接节点的边组成的数据结构。
在概率图模型中,一般用节点来表示一个或者一组随机变量,而节点之间的边则表示两个(组)变量之间的概率相关关系。
边可以是有向(有方向)的,也可以是无向的。概率图模型大致可以分为下面两类。
- 有向图模型(贝叶斯网络):用有向无环图表示变量间的依赖关系
- 无向图模型(马尔可夫网络):用无向图表示变量间的相关关系
HMM 就是贝叶斯网络的一种,虽然它的名字里有“马尔可夫”。对变量序列建模的贝叶斯网络又叫作动态贝叶斯网络。HMM 就是最简单的动态贝叶斯网络。
马尔可夫链,马尔可夫随机场和 CRF
马尔可夫链(markovchain)是一个随机过程模型,它表述了一系列可能的事件,在这个系列中,每一个事件的概率仅依赖前一个事件。
15.2 数学中的HMM
HMM是一个关于时序的概率模型,变量分为状态变量和观测变量
状态变量和观测变量各自是一个时间序列,每个状态值或观测值都与一个时刻对应,如图所示(箭头表示依赖关系)
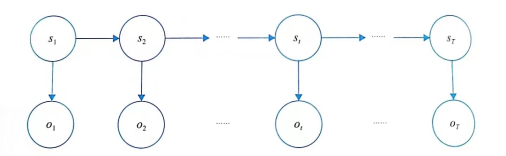
一般假定状态序列是隐藏的、不能被观测到的,所以状态变量就是隐变量(hidden variable)。这就是HMM 中H(hidden)的来源。这个隐藏的、不可观测的状态序列是由一个马尔可夫链随机生成的,这是HMM中的第一个M(markov)的含义。
一条隐藏的马尔可夫链随机生成一个不可观测的状态序列(statesequence),然后每个状态又对应生成一个观测结果,这些观测值按照时间顺序排列后就成了观测序列(observation sequence)。状态序列和观测序列一一对应,每个对应的位置又对应着一个时刻。
一般而言,HMM 状态变量的取值是离散的,而观测变量的取值可以是离散的,也可以是连续的。不过为了方便讨论,也因为在大多数应用中观测变量是离散的,我们下面仅讨论状态变量和观测变量都是离散的情况。
HMM的两个基本假设
假设1: 齐次马尔可夫假设
假设隐藏的马尔可夫链在任意时刻t的状态只依赖于前一个时刻(t-1)的状态,与其他时刻的状态及观测无关,也与时刻t无关。
用公式表达就是:
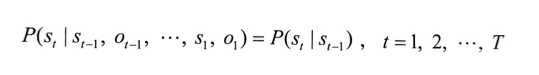
假设2:观测独立性假设
假设任意时刻的观测只依赖于该时刻的马尔可夫链状态,与其他观测无关。
用公式表达为:
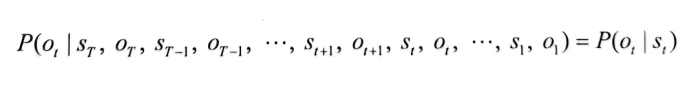
确定HMM的2个空间和3组参数
所有变量的联合分布为
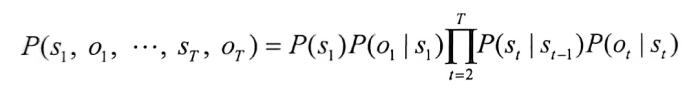

15.3 HMM的三个基本问题
概率计算问题
概率计算问题又称评价(evaluatior)问题。已知信息如下:
- 模型λ=(A,B,π)
- 观测序列O=(O1,O2,…,Oт)
求解目标:计算在给定模型λ下,已知观测序列O出现的概率:P(O|λ)。也就是说,给定观测序列,求它和评估模型之间的匹配度。
预测问题
预测问题又称解码问题。已知信息如下:
- 模型λ=(A,B,π)
- 观测序列O=(O1,O2,…,Oт)
求解目标:计算在给定模型λ下,使已知观测序列O的条件概率P(O|S)最大的状态序列S=(s1,S2,…,Sт)。即给定观测序列,求最有可能与之对应的状态序列。
学习问题
学习问题又称训练问题。已知信息如下:
- 观测序列O=(O1,O2,…,Oт)
此时,与O对应的状态序列:S=(s1,S2,…,sт)可能已知,也可能未知。
求解目标:估计模型λ=(A,B,π)参数,使得该模型下观测序列概率 P(O|λ) 最大。也就是训练模型,使其最好地描述观测数据。
前两个问题是模型已经存在之后,如何使用模型的问题,而最后一个是如何通过训练得到模型的问题。
15.4 HMM3个基本问题的计算
概率计算问题
可参考下文
HMM的概率计算问题_Joyliness的博客-CSDN博客_hmm概率计算
预测问题
使用维特比算法
可参考下文
如何通俗地讲解 viterbi 算法? - 知乎
学习问题
HMM 的学习算法根据训练数据的不同,可以分为有监督学习和无监督学习。
如果训练数据既包括观测序列,又包括对应的状式态序列,且两者之间的对应关系已经明确标注了出来,那么就可以用有监督学习算法。
如果只有观测序列而没有明确对应的状态序列, 就需要用无监督学习算法
可参考
HMM的Baum-Welch算法和Viterbi算法公式推导细节_Orange先生的博客-CSDN博客
15.6 HMM实例
from __future__ import division
import numpy as np
from hmmlearn import hmm
def calculateLikelyHood(model, X):
score = model.score(np.atleast_2d(X).T)
print("\n\n[CalculateLikelyHood]: ")
print("\nobservations:")
for observation in list(map(lambda x: observations[x], X)):
print(" ", observation)
print ("\nlikelyhood:", np.exp(score))
def optimizeStates(model, X):
Y = model.decode(np.atleast_2d(X).T)
print("\n\n[OptimizeStates]:")
print("\nobservations:")
for observation in list(map(lambda x: observations[x], X)):
print(" ", observation)
print("\nstates:")
for state in list(map(lambda x: states[x], Y[1])):
print(" ", state)
states = ["Gold", "Silver", "Bronze"]
n_states = len(states)
observations = ["Ruby", "Pearl", "Coral", "Sapphire"]
n_observations = len(observations)
start_probability = np.array([0.3, 0.3, 0.4])
transition_probability = np.array([
[0.1, 0.5, 0.4],
[0.4, 0.2, 0.4],
[0.5, 0.3, 0.2]
])
emission_probability = np.array([
[0.4, 0.2, 0.2, 0.2],
[0.25, 0.25, 0.25, 0.25],
[0.33, 0.33, 0.33, 0]
])
model = hmm.MultinomialHMM(n_components=3)
# 直接指定pi: startProbability, A: transmationProbability 和B: emissionProbability
model.startprob_ = start_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probability
X1 = [0,1,2]
calculateLikelyHood(model, X1)
optimizeStates(model, X1)
X2 = [0,0,0]
calculateLikelyHood(model, X2)
optimizeStates(model, X2)