算法复杂度

对于同一个问题，我们往往其实有很多种解决它的思路和方法，也就是可以采用不同的算法

• 但是不同的算法，其实效率是不一样的

举个例子（现实的例子）:在一个庞大的图书馆中，我们需要找一本书。在图书已经按照某种方式摆好的情况下（数据结构是固定的）

• 方式一：顺序查找
  • 一本本找，直到找到想要的书（累死）
• 方式二：先找分类，分类中找这本书
  • 先找到分类，在分类中再顺序或者某种方式查找
• 方式三：找到一台电脑，查找书的位置，直接找到
  • 图书馆通常有自己的图书管理系统
  • 利用图书管理系统先找到书的位置，再直接过去找到

顺序查找

方式一: 顺序查找

• 这种算法从头到尾遍历整个数组，依次比较每个元素和给定元素的值
• 如果找到相等的元素，则返回下标；如果遍历完整个数组都没找到，则返回 -1

function sequentSearch(array: number[], num: number) {
  for (let i = 0; i < array.length; i++) {
    const item = array[i]
    if (item === num) return i
  }
  return -1
}

二分查找

方式二：二分查找

• 这种算法假设数组是有序的，每次选择数组中间的元素与给定元素进行比较
• 如果相等，则返回下标；如果给定元素比中间元素小，则在数组的左半部分继续查找
• 如果给定元素比中间元素大，则在数组的右半部分继续查找
• 这样每次查找都会将查找范围减半，直到找到相等的元素或者查找范围为空

function binarySearch(array: number[], num: number) {
  // 1.定义左边的索引
  let left = 0
  // 2.定义右边的索引
  let right = array.length - 1
  // 3.开始查找
  while (left <= right) {
    let mid = Math.floor((left + right) / 2)
    const midNum = array[mid]
    if (midNum === num) {
      return mid
    } else if (midNum < num) {
      left = mid + 1
    } else {
      right = mid - 1
    }
  }
  return -1
}

测试效率

import sequentSearch from './1.顺序查找'
import binarySearch from './2.二分查找'

const MAX_LENGTH = 10 * 1000 * 1000
const nums = new Array(MAX_LENGTH).fill(0).map((_, i) => i)
const num = MAX_LENGTH / 2

const startTime1 = performance.now()
const index1 = sequentSearch(nums, num)
const endTime1 = performance.now()
console.log('索引为：', index1, '。消耗的时间：', endTime1 - startTime1)

const startTime2 = performance.now()
const index2 = binarySearch(nums, num)
const endTime2 = performance.now()
console.log('索引为：', index2, '。消耗的时间：', endTime2 - startTime2)

大O表示法

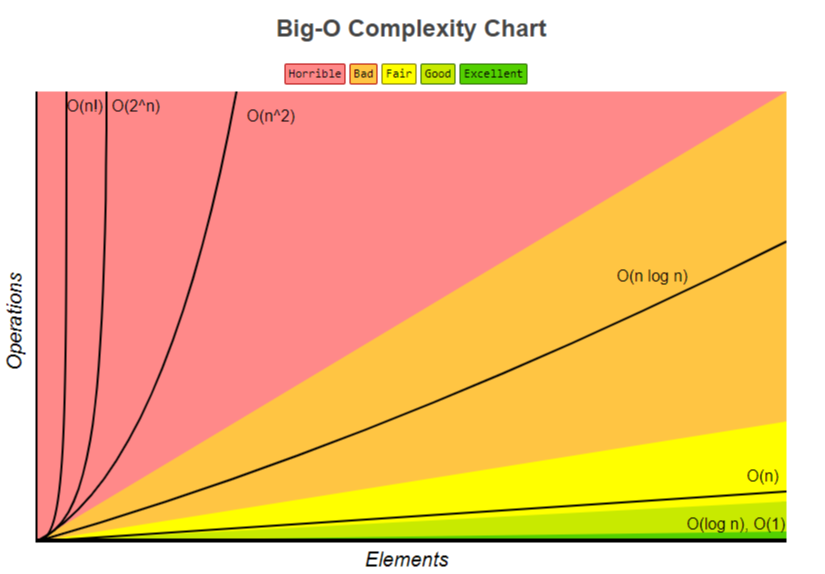
大 O 表示法（Big O notation）英文翻译为大 O 符号（维基百科翻译），中文通常翻译为大 O 表示法（标记法）

• 这个记号则是在德国数论学家爱德蒙·兰道的著作中才推广的，因此它有时又称为兰道符号（Landau symbols）
• 代表 “order of…” (…阶) 的大 O，最初是一个大写希腊字母 “O” (omicron) ，现今用的是大写拉丁字母 “O”

大 O 符号在分析算法效率的时候非常有用

举个例子，解决一个规模为 n 的时间所花费的时间（或者所需步骤的数目）可以表示为：T(n) = 4n^2 -2n + 2

• 当 n 增大时，n^2 项开始占据主导地位，其他各项可以被忽略

举例说明：当 n=500

• 4n^2 项是 2n 项的 1000 倍大，因此在多数场合下，省略后者对表达式的值的影响是可以忽略不计的
• 进一步看，如果我们与任意其他级的表达式比较，n^2 的系数也是无关紧要的

这样，针对这个例子 T(n) = 4n^2 -2n + 2 大 O 表示法就几下剩余的部分，写作：T(n) = O(n^2)

• 具有 n^2（平方阶）的时间复杂度，表示为：O(n^2)

函数阶

符号	名称
O(1)	常数（阶）
O(log^n)	对数（阶）
O(n)	线性，次线性
O(n log^n)	线性对数，或对数线性、拟线性、超线性
O(n^2)	平方
O(n^c)	多项式，有时叫作 “代数”（阶）
O(c^n)	指数，有时叫做 “几何”（阶）

空间复杂度

空间复杂度指的是程序运行过程中所需要的额外存储空间

• 空间复杂度也可以用大 O 表示法来表示
• 空间复杂度的计算方法与时间复杂度类似，通常需要分析程序中需要额外分配的内存空间，如数组、变量、对象、递归调用等

举个栗子

• 对于一个简单的递归算法来说，每次调用都会在内存中分配新的栈帧，这些栈赖占用了额外的空间
  • 因此，该算法的空间复杂度是 O(n)，其中 n 是递归深度
• 而对于迭代算法来说，在每次迭代中不需要分配额外的空间，因此其空间复杂度为 O(1)

当空间复杂度很大时，可能会导致内存不足，程序崩溃

在平时进行算法优化时，我们通常会进行如下的考虑：

• 使用尽量少的时间（优化空间复杂度）
• 使用进行少的时间（优化时间复杂度）
• 特定情况下：使用空间换时间或时间换空间

	数组	链表
访问	O(1)	O(n)
查询	O(n)	O(n)
插入	O(n)	O(1)
删除	O(n)	O(1)

数组是一种连续的存储结构，通过下标可以直接访问数组中的任意元素

• 时间复杂度：对于数组，随机访问时间复杂度为 O(1)，插入和删除操作时间复杂度为 O(n)
• 空间复杂度：数组需要连续的存储空间，空间复杂度为 O(n)

链表是一种链式存储结构，通过指针链接起来的节点组成，访问链表中元素需要从头结点开始遍历

• 时间复杂度：对于链表，随机访问时间复杂度为 O(n)，插入和删除操作时间复杂度为 O(1)
• 空间复杂度：链表需要为每个节点分配存储空间，空间复杂度为 O(n)

在实际开发中，选择使用数组还是链表，需要根据具体应用场景来决定

• 如果数据量不大，且需要频繁随机访问元素，使用数组可能会更好
• 如果数据量大，或者需要频繁插入和删除元素，使用链表可能会更好

哈希表

哈希表通常是基于数组进行实现的，但是相对于数组，它也有很多优势：

• 它可以提供非常快速的插入-删除-查找操作
• 无论多少数据，插入和删除值都接近常量的时间：即 O(1) 的时间复杂度。实际上，只需要几个机器指令即可完成
• 哈希表的速度比数还要快，基本可以瞬间查找到想要的元素
• 哈希表相对于数来说编码要容易很多

哈希表相对于数组的一些不足：

• 哈希表中的数据是没有顺序的，所以不能以一种固定的方式（比如从小到大）来遍历其中的元素（没有特殊处理情况下）
• 通常情况下，哈希表中的 key 是不允许重复的，不嫩放置相同的 key，用于保存不同的元素

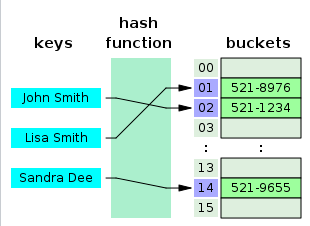
哈希表它的结构就是数组，但是它神奇的地方在于对数组下标值的一种变换，这种变换我们可以使用哈希函数，通过哈希函数可以获取到 HashCode

案例

公司员工存储

方案一：数组

• 一种方案是按照顺序将所有的员工依次存入一个长度为 1000 的数组中
• 每个员工的信息都保存在数组的某个位置上
• 数组最大的优势是什么？通过下标值去获取信息
• 为了可以通过数组快速定位到某个员工，最好给员工信息中添加一个员工编号，而编号对应的就是员工的下标值
• 当查找某个员工的信息时，通过员工编码可以快速定位到员工的信息位置

方案二：链表

• 链表对应插入和删除数据有一定优势
• 但是对于获取员工的信息，每次都必须从头遍历到尾

如果我们知道员工的姓名，但不知道它的员工编号，只能线性查找，效率非常低

• 使用哈希函数，让某个 key 的信息和索引值对应起来

50000个单词的存储

方案一：数组

• 我拿到一个单词 lridescent，我想知道这个单词的翻译/读音/应用
• 怎么可以从数组中查到这个单词的位置呢？线性查找？50000次比较？
• 如果你使用数组来实现这个功能，效率会非常非常低

方案二：链表

• 不需要考虑

方案三：将单词转成数组的下标值

• 如果单词转成数组下标，那么我们要查找某个单词的信息，直接按照下标值一步即可访问到想要的元素

字母转数字

字符串转下标值

• 计算机中有很多编码方案用数字代替单词字符，就是字符编码，比如 ASII 编码。a 是 97，b 是 98，z 是 122
• 当然也可以自己设计编码系统，比如 a 是 1，b 是 2，z 是 26

方案一：数字想加

• 一种转换单词的简单方案就是把单词每个字符的编码求和
• 比如：cats: 3 + 1 + 20 + 19 = 43，这种方案明显的问题就是有很多单词最终的下标都是 43，比如：was/tin/give/tend/moan/tick 等等

方案二：幂的连乘

• 可以通过一种算法，让 cats 转成不那么普通的数字
• 我们平时使用的大于 10 的数字，可以用一种幂的连乘来表示它的唯一性
• 比如：cats: 3*27^3 + 1*27^2 + 20*27 + 17 = 60337
• 这样得到的数字可以基本保证它的唯一性，不会和别的单词重复
• 问题：如果一个单词是：zzzzzzzzzz，那么得到的数字超过 7000000000000，创建这么大的数组是没有意义的，这样就会导致空间浪费

方案一产生的数组下标太小，方案二产生的数组下标又太多

开放地址法

开放地址法主要工作方式是寻找空白的单元格来添加重复的数据

从图片的文字中我们可以了解到，开放地址法其实就是要寻找空白的位置来防止冲突的数据项

但是探索这个位置的方式不同，有三种方法

• 线性探测
  • 线性查找空白的单元
  • 问题：聚集，一连串填充单元叫聚集，连续的单元不允许我们放置数据
• 二次探测
  • 二次探测是在线性探测基础上对步长进行了优化
• 再哈希法
  • 二次探测步长依然是固定的，可以关键字用另外一个哈希函数，再做一次哈希化，用这次哈希化作为步长

链地址法

哈希表中执行插入和搜索操作效率是非常高的

• 如果没有产生冲突，那么效率就会更高
• 如果发生冲突，存取时间就依赖后来的探测长度
• 平均探测长度以及平均存取时间，取决于装填因子，随着装填因子变大，探测长度也越来越长
• 随着装填因子变大，效率下降的情况，在不同开放地址法方案中比链地址法更严重，所以我们来对比一下他们的效率，再决定我们选取的方案

装填因子

• 装填因子表示当前哈希表中已经包含的数据项和整个哈希表长度的比值
• 装填因子 = 总数据项 / 哈希表长度
• 开放地址法的装填肉子最大是多少呢？ 1，因为它必须寻找到空白的单元才能将元素放入
• 链地址法的装填因子呢？可以大于1，因为拉链法可以无限的延伸下去，只要你愿意。(当然后面效率就变低了)

线性探测效率

• 探测序列（P）和装填因子（L）的关系
• 公式来自于 Knuth（算法分析领域的专家，现代计算机的先驱人物），给出推导过程，仅仅说明它的效率。这些公式的推导自己去看了一下，确实有些繁琐

二次探测和再哈希法性能相当，它们的性能比线性探测略好

链地址法的效率分析有些不同，一般来说比开放地址法简单。我们来分析一下这个公式应该是怎么样的

• 假如哈希表包含 arraySize 个数据项，每个数据项有一个链表，在表中一共包含 N 个数据项
• 那么，平均起来每个链表有多少个数据项呢？非常简单，N / arraySize
• 有没有发现这个公式有点眼熟？其实就是装填因子

那么我们现在就可以求出查找成功和不成功的次数了

• 成功可能只需要查找链表的一半即可: 1 + loadFactor/ 2
• 不成功呢？可能需要将整个链表查询完才知道不成功: 1 + loadFactor

经过上面的比较我们可以发现，链地址法相对来说效率是好于开放地址法的。所以在真实开发中，使用链地址法的情况较多

• 因为它不会因为添加了某元素后性能急剧下降
• 比如在 Java 的 HashMap 中使用的就是链地址法

哈希函数

• 哈希表的主要优点是它的速度，所以在速度上不能满足，那么就达不到设计的目的了
• 提高速度的一个办法就是让哈希函数中尽量少的有乘法和除法。因为它们的性能是比较低的

快速的计算

• 哈希表的优势就在于效率，所以快速获取到对应的 hashCode 非常重要
• 我们需要通过快速的计算来获取到元素对应的 hashCode

均匀的分布

• 哈希表中，无论是链地址法还是开放地址法，当多个元素映射到同一个位置的时候，都会影响效率
• 所以，优秀的哈希函数应该尽可能将元素映射到不同的位置，让元素在哈希表中均匀的分布

均匀分布

• 在设计哈希表时，已经有办法处理映射到相同下标值的情况：链地址法和开放地址法
• 但是无论哪种方案，为了提供效率，最好的情况还是让数据在哈希表中均匀分布
• 因此，我们需要再使用常量的地方，尽量使用质数

质数的使用

• 哈希表的长度
• N 次幂的底数（之前使用的是 27）

为什么他们使用质数，会让哈希表分布更加均匀呢？

• 质数和其他数相乘的结果相比于其他数字更容易产生唯一性的结果，减少哈希冲突
• Java 中的 N 次幂的底数选择的是 31，是经过长期观察分布结果得出的。31 * i 可以用 (i << 5) - i 来计算，位移操作效率更高

Java中的hashCode的计算方法与原理

Java 中的 HashMap

Java 中的哈希表采用的是链地址法

HashMap 的初始长度是 16，每次自动扩展，长度必须是 2 的次幂

• 为了服务于 Key 映射到 index 的算法。60000000 % 100 = 数字。下标值

HashMap 中为了提高效率，采用了位运算的方式

• HashMap 中的 index 计算公式：index = HashCode(Key) & (Length - 1)
• 比如计算 book 的 hashcode，结果为十进制的 3029737，二进制的 101110001110101110 1001
• 假定 HashMap 长度是默认的 16，计算 Lenght - 1 的结果为十进制的 15，二进制的 1111
• 把以上两个结果做与运算，101110001110101110 1001 & 1111 = 1001，十进制是 9，所以 index=9

public static int hashCode(byte[] value) {
  int h = 0;
  for (byte v : value) {
    h = 31 * h + (v & 0xff);
  }
  return h;
}

Java 里是如上计算的，使用到了位运算，但是在 JavaScript 进行较大数据的位运算时会出问题，所以一下代码实现中还是使用取模

• 另外，为了方便代码之后向开放地址法中迁移，容量还是选择使用质数

这里采用质数的原因是为了产生的数据不按照某种规律递增

• 比如我们这里有一组数据是按照4进行递增的：0 4 8 12 16，将其映射到长度为 8 的哈希表中
• 它们的位置是多少呢? 0 -4 -0 4，依次类推
• 如果我们哈希表本身不是质数，而我们递增的数量可以使用质数，比如 5，那么0 5 10 15 20
• 它们的位置是多少呢? 0 -5 -2 -7 -4，依次类推。也可以尽量让数据均匀的分布
• 我们之前使用的是 27，这次可以使用一个接近的数，比如 31/37/41 等等。一个比较常用的数是 31 或 37

这里建议两处使用质数：

• 哈希表中数组的长度
• N 次幂的底数

/**
 * 哈希函数，将 key 映射成 index
 * @param key 转换的 key
 * @param max 数组的长度（最大的数值）
 * @returns
 */
function hashFunc(key: string, max: number): number {
  // 1.计算hashCode cats=>60337(27为底)
  let hashCode = 0
  const length = key.length
  for (let i = 0; i < length; i++) {
    // 霍纳法则计算 hashCode
    hashCode = 31 * hashCode + key.charCodeAt(i)
  }
  // 2.求出索引值
  const index = hashCode % max
  return index
}

HashMap 与 Hashtable 区别

1. 同步性、安全性

   • Hashtable 方法都加了 synchronized（同步器），线程都需要排队进行所以线程安全
   • HashMap 非线程安全，性能会更好

   

2. 继承父类不同

   • Hashtable 继承于 Dictionary
   • HashMap 继承于 AbstractMap

   

   

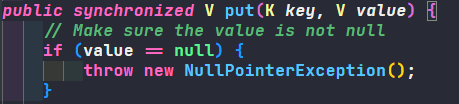
3. 否可以使用 null 作为 key

   • Hashtable 会选判断一下 value 的值不为 null，如果为 null 会报空指针异常
   • HashMap key 可以为 null，计算下标为 0

   
   

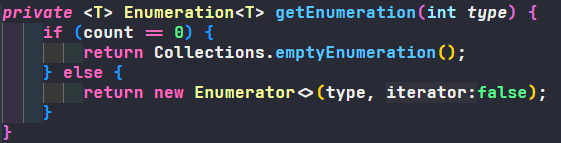
4. 遍历方式不同

   • Hashtable 使用 Enumeration 遍历
   • HashMap 使用 Iterator 遍历

   

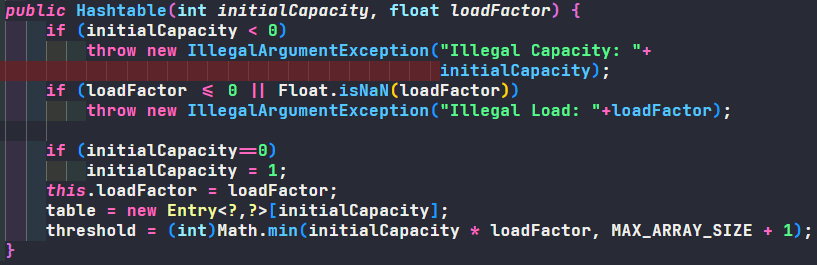
5. 初始化、扩容方式不同

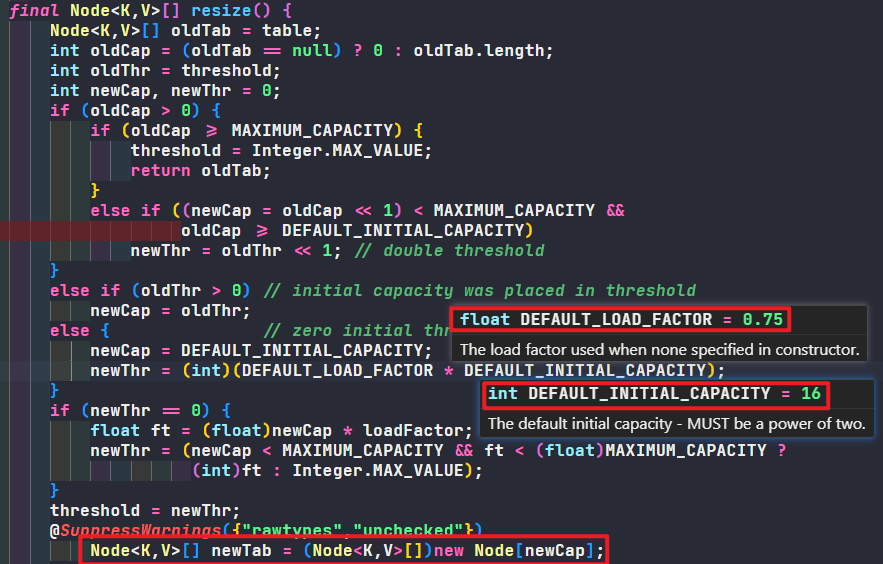
   • Hashtable 默认初始大小为 11，在调用构造函数中初始化，每次扩容都是向左位移一位再加一（<<1+1 -> *2+1）
   • HashMap 默认初始大小是 16，没有在调用构造函数中初始化，在第一次调用 put 之后才会初始化，每次扩容都是向左位移一位（<<1 -> *2），并且要求容量是 2^n，保证计算下标效率

   

   

   

6. 计算 hash 方式不同

   • Hashtable 计算 hash 是直接使用 key 的 hashcode 之后与数组的长度直接进行取余

     0x7FFFFFFF 最大整型树

   • HashMap 计算 hash 对 key 的 hashcode 进行了二次 hash（取哈希值并高位向右移进行异或运算），然后与数组长度取模

     HashMap 效率虽然提高了，但是 hash 冲突也增加了，因为它得出的 hash 的低位相同的概率比较高，而计算位运算解决这个问题，HashMap 重新根据 hashcode 计算 has 值后，又对 hash 做了一些运算来打散数据，使得取得的位置更加分散，从而减少 hash 冲突

   

   

   

7. 内部实现方式不同

   • Hashtable 使用数组+链表
   • HashMap 采用数组+链表+红黑树

HashMap

1. HashMap 底层是采用了数组这样一个结构来存储数据元素，数据默认长度是 16

2. 当我们通过 put 方法去添加数据的时候，HashMap 会根据 Key 的 hash 值进行取模运算，最终把这样的一个值保存到数组一个指定位置

3. 但是这样一个设计方式会存在 hash 冲突问题，也就是说两个不同 hash 值的 key 最终取模以后会落到同一个数组下标

4. 所以 HashMap 引入了一个链式寻址法来解决 hash 冲突问题，也就是对于存在冲突的 key，HashMap 把这些 key 组成一个单向链表，然后采用尾插法，把这样一个 key 保存到链表的尾部

5. 为了避免链表过长，导致查询效率下降，所以当链表大于 8 并且数组长度大于等于 64 的时候，HashMap 会把当前链表转换为红黑树，从而减少链表数据查询的时间复杂度，提升查询效率

6. 解决 hash 冲突方法有很多

   • 再 hash 法：如果某个 hash 函数产生了冲突，再用另外一个 hash 进行计算，比如布隆过滤器就采用了这种方法

   • 开放寻址法，就是直接从冲突的数组位置往下寻找一个空的数组下标进行数据存储，这个在 ThreadLocal 里面有使用到

   • 链式寻址法，就是把存在 hash 冲突的 key 以单向链表的方式来进行存储，这个在 HashMap 里面有使用到

     在 JDK1.8 中使用链式寻址法及红黑树来解决 hash 冲突问题，红黑树是为了优化 hash 表链表过长导致时间复杂度增加的一个问题。当链表长度大于 8，并且 hash 表的容量大于 64 的时候再向链表中添加元素就会触发链表向红黑树的转化

   • 建立公共溢出区，把 hash 表分为基本表、溢出表两个部分，把存在冲突的 key 统一放在一个公共溢出表里面

总结

• 长度不够会动态扩容，threshold（临界值）=loadFactor（负载因子）*capacity（容量大小）

  loadFactor 默认值 0.75，capacity 默认值 16，当元素个数达到 12 的时候会触发扩容，扩容的大小是原来的 2 倍

• 扩容因子表示 Hash 表中的元素填充程度。扩容因子值越大意味着触发扩容的元素个数更多，虽然整体空间利用率比较高，但是 Hash 冲突的概率也会增加，扩容因子越小，Hash 冲突概率越小，但是内存空间的浪费就变多了。扩容因子本质上就是冲突的概率以及空间利用率之间的平衡，0.75 和统计学泊松分布

  HashMap 里面采用的是链式寻址的方式解决 Hash 冲突，为了避免链表过长带来一个时间复杂度增加的情况，链表长度 >=7 就会转换红黑树，提升检索效率。扩容因子在 0.75 时，链表长度达到 8 的可能几乎为 0，比较好的达到一个空间成本和时间成本的平衡

• 最大容量是 Integer.MAX_VALUE，即 2^31 - 1

哈希表实现

这里采用链地址法实现哈希表

• 实现的哈希表（基于 storage 的数组）每个 index 对应的是一个数组（bucket）
• bucket 中存放什么呢？我们最好将 key 和 value 都放进去，我们继续使用一个数组
• 最终我们的哈希表的数据格式是这样：[[[k, v], [k, v], [k, v]]]

哈希表的插入和修改操作是同一个函数

• 因为，当使用者传入一个 <Key, Value> 时
• 如果原来不存该 key，那么就是插入操作
• 如果已经存在该 key，那么就是修改操作

删除数据

• 根据对应的 key，删除对应的 key/value

class HashTable<T = any> {
  // 创建一个数组，用来存放链地址法中的链（数组）
  private storage: [string, T][][] = []
  // 定义数组的长度
  private length: number = 7
  // 记录已经存放元素的个数
  private count: number = 0
  // 计算索引值
  private getIndex(key: string, max: number): number {
    let hashCode = 0
    const length = key.length
    for (let i = 0; i < length; i++) {
      // 霍纳法则计算 hashCode
      hashCode = 31 * hashCode + key.charCodeAt(i)
    }
    const index = hashCode % max
    return index
  }

  // 插入/修改
  put(key: string, value: T) {
    // 1.根据key获取数组中对应的索引值
    const index = this.getIndex(key, this.length)
    // 2.取出索引值对应位置的数组（桶）
    let bucket = this.storage[index]
    // 3.判断bucket是否有值
    if (!bucket) {
      bucket = []
      this.storage[index] = bucket
    }
    // 4.确定已经有一个数组，但是数组中是否已经存在key是不确定的
    let isUpdate = false
    for (let i = 0; i < bucket.length; i++) {
      const tuple = bucket[i]
      const tupleKey = tuple[0]
      if (tupleKey === key) {
        isUpdate = true
        tuple[1] = value
      }
    }
    // 5.如果上面的代码没有进行覆盖，那么在该位置进行添加
    if (!isUpdate) {
      bucket.push([key, value])
      this.count++
    }
  }

  // 获取值
  get(key: string): T | undefined {
    // 1.根据key获取索引值index
    const index = this.getIndex(key, this.length)
    // 2.获取bucket（桶）
    const bucket = this.storage[index]
    if (!bucket) return undefined
    // 3.对bucket进行遍历
    for (let i = 0; i < bucket.length; i++) {
      const tuple = bucket[i]
      const tupleKey = tuple[0]
      const tupleValue = tuple[1]
      if (tupleKey === key) {
        return tupleValue
      }
      return undefined
    }
  }

  // 删除操作
  delete(key: string): T | undefined {
    // 1.获取索引值的位置
    const index = this.getIndex(key, this.length)
    // 2.获取bucket（桶）
    const bucket = this.storage[index]
    if (!bucket) return undefined
    for (let i = 0; i < bucket.length; i++) {
      const tuple = bucket[i]
      const tupleKey = tuple[0]
      const tupleValue = tuple[1]
      if (tupleKey === key) {
        bucket.splice(i, 1)
        this.count--
        return tupleValue
      }
    }
  }
}

哈希表扩容

为什么需要扩容？

• 目前，我们是将所有的数据项放在长度为 7 的数组中的
• 因为我们使用的是链地址法，loadFactor 可以大于 1，所以这个哈希表可以无限制的插入新数据
• 但是，随着数据量的增多，每一个 index 对应的 bucket 会越来越长，也就造成效率的降低
• 所以，在合适的情况对数组进行扩容，比如扩容两倍

如何进行扩容？

• 扩容可以简单的将容量增大两倍（但是这里变大两倍会出现不是质数问题）
• 但是这种情况下，所有的数据项一定要同时进行修改（重新调用哈希函数，来获取到不同的位置）
• 比如 hashCode=12 的数据项，在 length=8 的时候，index=4。在长度为 16 的时候呢？index=12
• 这是一个耗时的过程，但是如果数组需要扩容，那么这个过程是必要的

class HashTable<T = any> {
  private resize(newLength: number) {
    // 设置新的长度
    this.length = newLength
    // 获取原来所有的数据，并且重新放入到新的容量数组中
    // 1.对数据进行初始化操作
    const oldStorage = this.storage
    this.storage = []
    this.count = 0
    // 2.获取原来数，放入新的数组中
    oldStorage.forEach(bucket => {
      if (!bucket) return
      for (let i = 0; i < bucket.length; i++) {
        const tuple = bucket[i]
        this.put(tuple[0], tuple[1])
      }
    })
  }
  put(key: string, value: T) {
    if (!isUpdate) {
      // 如果loadFactor大于0.75，扩容操作
      const loadFactor = this.count / this.length
      if (loadFactor > 0.75) {
        this.resize(this.length * 2)
      }
    }
  }
  delete(key: string): T | undefined {
    for (let i = 0; i < bucket.length; i++) {
      if (tupleKey === key) {
        // 如果loadFactor小于0.25，缩容操作
        const loadFactor = this.count / this.length
        if (loadFactor < 0.25 && this.length > 7) {
          this.resize(Math.floor(this.length / 2))
        }
      }
    }
  }
}

容量质数

容量最好是质数

• 虽然在链地址法中将容量设置为质数，没有在开放地址法中重要
• 但是其实链地址法中质数作为容量也更利于数据的均匀分布

质数的特点

• 质数也称为素数
• 质数表示大于 1 的自然数中，只能被 1 和自己整除的数

class HashTable<T = any> {
  private isPrime(num: number): boolean {
    const sqrt = Math.sqrt(num)
    for (let i = 2; i <= sqrt; i++) {
      if (num % i === 0) {
        return false
      }
    }
    return true
  }
  private getNextPrime(num: number) {
    let newPrime = num
    while (!this.isPrime(newPrime)) {
      newPrime++
    }
    if (newPrime < 7) newPrime = 7
    return newPrime
  }
  private resize(newLength: number) {
    this.length = this.getNextPrime(newLength)
  }
}

完整代码

class HashTable<T = any> {
  // 创建一个数组，用来存放链地址法中的链（数组）
  storage: [string, T][][] = []
  // 定义数组的长度
  private length: number = 7
  // 记录已经存放元素的个数
  private count: number = 0
  // 计算索引值
  private getIndex(key: string, max: number): number {
    let hashCode = 0
    const length = key.length
    for (let i = 0; i < length; i++) {
      // 霍纳法则计算 hashCode
      hashCode = 31 * hashCode + key.charCodeAt(i)
    }
    const index = hashCode % max
    return index
  }
  // 获取下一个质数
  private getNextPrime(num: number) {
    let newPrime = num
    while (!this.isPrime(newPrime)) {
      newPrime++
    }
    if (newPrime < 7) newPrime = 7
    return newPrime
  }
  // 扩容/缩容
  private resize(newLength: number) {
    // 设置新的长度
    this.length = this.getNextPrime(newLength)
    console.log(this.length, 'new')

    // 获取原来所有的数据，并且重新放入到新的容量数组中
    // 1.对数据进行初始化操作
    const oldStorage = this.storage
    this.storage = []
    this.count = 0
    // 2.获取原来数，放入新的数组中
    oldStorage.forEach(bucket => {
      if (!bucket) return
      for (let i = 0; i < bucket.length; i++) {
        const tuple = bucket[i]
        this.put(tuple[0], tuple[1])
      }
    })
  }
  // 是否是质数
  private isPrime(num: number): boolean {
    // 质数的特点：只能被1和num整除
    const sqrt = Math.sqrt(num)
    for (let i = 2; i <= sqrt; i++) {
      if (num % i === 0) {
        return false
      }
    }
    return true
  }
  // 插入/修改
  put(key: string, value: T) {
    // 1.根据key获取数组中对应的索引值
    const index = this.getIndex(key, this.length)
    // 2.取出索引值对应位置的数组（桶）
    let bucket = this.storage[index]
    // 3.判断bucket是否有值
    if (!bucket) {
      bucket = []
      this.storage[index] = bucket
    }
    // 4.确定已经有一个数组，但是数组中是否已经存在key是不确定的
    let isUpdate = false
    for (let i = 0; i < bucket.length; i++) {
      const tuple = bucket[i]
      const tupleKey = tuple[0]
      if (tupleKey === key) {
        isUpdate = true
        tuple[1] = value
      }
    }
    // 5.如果上面的代码没有进行覆盖，那么在该位置进行添加
    if (!isUpdate) {
      bucket.push([key, value])
      this.count++
      // 如果loadFactor大于0.75，扩容操作
      const loadFactor = this.count / this.length
      if (loadFactor > 0.75) {
        this.resize(this.length * 2)
      }
    }
  }
  // 获取值
  get(key: string): T | undefined {
    // 1.根据key获取索引值index
    const index = this.getIndex(key, this.length)
    // 2.获取bucket（桶）
    const bucket = this.storage[index]
    if (!bucket) return undefined
    // 3.对bucket进行遍历
    for (let i = 0; i < bucket.length; i++) {
      const tuple = bucket[i]
      const tupleKey = tuple[0]
      const tupleValue = tuple[1]
      if (tupleKey === key) {
        return tupleValue
      }
      return undefined
    }
  }
  // 删除操作
  delete(key: string): T | undefined {
    // 1.获取索引值的位置
    const index = this.getIndex(key, this.length)
    // 2.获取bucket（桶）
    const bucket = this.storage[index]
    if (!bucket) return undefined
    for (let i = 0; i < bucket.length; i++) {
      const tuple = bucket[i]
      const tupleKey = tuple[0]
      const tupleValue = tuple[1]
      if (tupleKey === key) {
        bucket.splice(i, 1)
        this.count--
        // 如果loadFactor小于0.25，缩容操作
        const loadFactor = this.count / this.length
        if (loadFactor < 0.25 && this.length > 7) {
          this.resize(Math.floor(this.length / 2))
        }
        return tupleValue
      }
    }
  }
}