题面
[USACO07DEC] Sightseeing Cows G - 洛谷
题目大意:
给出一张n点m边的带点权带边权的有向图
求一个回路使得路上点权和除以边权和最大(最优比率回路)
题解
首先一定仔细读题,是回路不是路径
由于回路上所有点权只能获取一次,但边权会获取很多次,所以最优解一定是简单回路(无重复边)
然后我们发现是让一个分数最大,于是我们可以考虑分数规划二分
假设二分的商为mid,判断是否存在一个满足点边权和比大于mid的回路,则二分判断条件为
(Vp为最优简单回路的点集,Ep为最优简单回路的边集)
稍微变换一下形式
这个判断条件依旧不好计算,因为我们二分的目的就是为了把最优化问题转换为判断性问题,但是对于该条件,我们除了枚举所有的简单回路,没有任何切入点
转念一想,最后这个大于0似乎暗藏玄机,又和回路联系在一起
不由得让人想到判断图是否存在正权回路(可以直接取相反数转化为判断负权回路)
为了把问题往这个方向转,我们尝试把点权下放到边权
把每条边边权设置为 -(它要通往的点的点权-mid*它原本的边权)
但是这样又会有一个新的问题,如果我们最后选出来的回路是这个样子
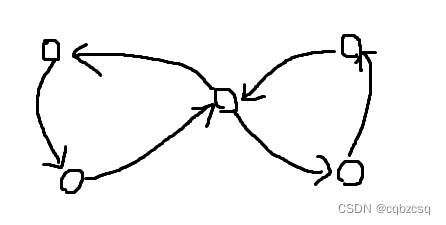
这样不就会重复计算点权了吗?
事实上这种情况是不存在的
我们可以感性的证明一下:
出现重复点的简单回路,一定可以拆解成若干初级回路(无重复点、无重复边)
整个回路最终的比率一定不会超过其中比率最大的初级回路((a+b)/(c+d)<=max(a/c,b/d),似乎在小学奥数里面叫糖水不等式?)(而且整个回路的比率的分子还会减去重复点的点权)
所以,我们选择一定是选择简单回路里面最优的初级回路
至此,我们就可以下放点权了
愉快地使用SPFA进行负权回路判断
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
#define N 1005
#define M 10005
#define INF 1000000000
int n,m;
int F[N];
struct enode{
int u,v,w;
}E[M];
int fir[N],to[M],nxt[M],cnt;
double cd[M];
void adde(int a,int b,double c)
{
to[++cnt]=b;cd[cnt]=c;nxt[cnt]=fir[a];fir[a]=cnt;
}
double dis[N];
int con[N];
bool inq[N];
queue<int> Q;
bool check()
{
int i;
for(i=1;i<=n;i++)dis[i]=INF;
for(i=1;i<=n;i++)con[i]=0;
for(i=1;i<=n;i++)inq[i]=0;
for(i=1;i<=n;i++){
if(dis[i]==INF){
dis[i]=0;inq[i]=1;
Q.push(i);
while(!Q.empty()){
int u=Q.front();Q.pop();inq[u]=0;
for(int p=fir[u];p;p=nxt[p]){
int v=to[p];
double w=cd[p];
if(dis[u]+w<dis[v]){
dis[v]=dis[u]+w;
con[v]++;
if(!inq[v]){Q.push(v);inq[v]=1;}
if(con[v]>=n)return 1;
}
}
}
}
}
return 0;
}
int main()
{
int i;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
scanf("%d",&F[i]);
for(i=1;i<=m;i++)
scanf("%d%d%d",&E[i].u,&E[i].v,&E[i].w);
double l=0,r=1000,mid;
while(r-l>1e-3){
mid=(l+r)/2;
cnt=0;
for(i=1;i<=n;i++)fir[i]=0;
for(i=1;i<=m;i++)
adde(E[i].u,E[i].v,-(1.0*F[E[i].v]-mid*E[i].w));
if(check())
l=mid;
else
r=mid;
}
printf("%.2f",l);
}