一、题目描述

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

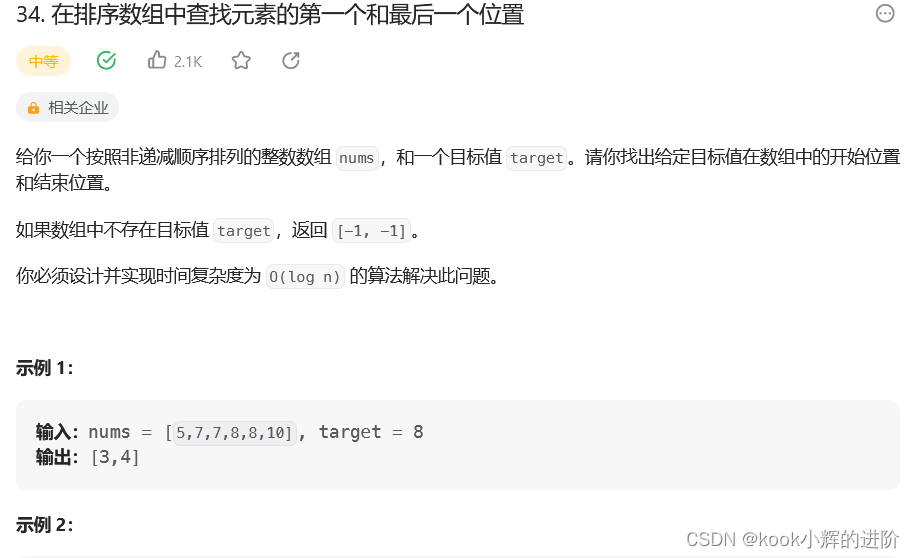
解题思路：1、按题意可知必须写一个时间复杂度为O（log n）的算法，如果不限定的话，直接遍历累加target数量返回下标就过于简单了。

2、我们使用二分查找可以满足时间复杂度的要求，这里先讲解一个简单版，便于理解。

【简易版】

1、新建一个result数组用于返回。

2、确定两个边界left、right为数组开头和结尾元素。

3、在两个指针相遇前分别进行遍历

4、分别可以获得第一个target下标和最后一个target下标

public int[] searchRange2(int[] nums, int target) {//简单解法，时间复杂度高
            int[] result = new int[] {-1, -1};//创建新数组用于返回
            int right = nums.length - 1;//右边界
            int left = 0;//左边界
            while (left <= right) {
                if (nums[left] == target && nums[right] == target) {
                    result[0] = left;//获得第一个target下标
                    result[1] = right;//最后一个target下标
                    break;
                }
                if (nums[left] < target) {//向左遍历
                    left++;
                }
                if (nums[right] > target) {//向右遍历
                    right--;
                }
            }
            return result;
        }

【进阶版】

1、进阶解法本质也是二分查找，通过两次左右边界的查找，来确定target的范围。

2、通过第一次查找左边界target位置。

3、通过查找target右边的一个元素位置，即间接的获得最后一个target的下标。

4、需满足左边界小于等于右边界，且右边界不超出数组长度，且两个边界值均为target。

public int[] searchRange(int[] nums, int target){
        if (nums.length==0)
            return new int[]{-1,-1};
        int LeftInd=BinarySearch(nums,target);//左边target下标
        int RightInd=BinarySearch(nums,target+1)-1;//右边界target下标
       if (LeftInd<=RightInd&&RightInd<=nums.length&&nums[LeftInd]==target&&nums[RightInd]==target)
            return new int[]{LeftInd,RightInd};
       else   return new int[]{-1,-1};
    }
    public int BinarySearch(int nums[],int target){
        int left=0;
        int right=nums.length;
        while (left<right){
            int mid=left+(right-left)/2;
            if (target<=nums[mid]){逐渐左移，找到最左边的target
                right=mid;
            }
            else  left=mid+1;
        }
        return left;//返回的是第一个target下标
    }