目录
KNN算法
1、简介
2、原理分析
数学原理
相关公式及其过程分析
距离度量
k值选择
分类决策规则
3、API
4、⭐案例实践
4.1、分析
4.2、代码
5、K-近邻算法总结
🍃作者介绍:准大三网络工程专业在读,努力学习Java,涉猎深度学习,积极输出优质文章
⭐分类算法系列①:初识概念
KNN算法
定义:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
来源:KNN算法最早是由Cover和Hart提出的一种分类算法
1、简介
K最近邻(K-Nearest Neighbors,KNN)是一种简单但强大的监督学习算法,用于分类和回归任务。它的基本思想是:给定一个新的数据点,通过找到训练数据中最接近它的K个邻居,来进行分类或回归预测。KNN算法在许多实际问题中表现良好,但也有其局限性。
以下是KNN算法的基本工作原理:
- 数据表示: 对于每个样本,KNN使用一组特征来描述。这些特征可以是数值、类别或其他类型的数据。每个样本都由特征向量表示。
- 距离度量: KNN算法使用某种距离度量来计算数据点之间的相似性。常用的距离度量包括欧几里德距离、曼哈顿距离等。对于每个样本,都可以计算其与训练数据中其他样本之间的距离。
- 邻居选择: 对于一个新的数据点,KNN算法会计算它与训练数据中所有数据点的距离,并选择最近的K个邻居。这些邻居通常是距离最近的K个训练样本。
- 预测(分类问题): 对于分类问题,KNN算法会将这K个最近邻居的类别进行统计,然后将新数据点分类为在这些邻居中占多数的类别。这就是所谓的“多数投票”法。
- 预测(回归问题): 对于回归问题,KNN算法会将这K个最近邻居的目标值(即回归目标)进行平均,然后将新数据点的回归预测设置为这个平均值。
KNN算法的优点包括简单易用、适用于多类别分类、不需要训练阶段(直接存储训练数据)等。
然而,KNN算法也有一些缺点,包括:
- 效率问题:对于大规模数据集,计算所有样本之间的距离可能会很耗时。
- 高维数据:在高维特征空间中,距离计算变得困难,且容易出现维度灾难(curse of dimensionality)。
- 需要合适的距离度量和K值的选择。
在实际应用中,选择适当的K值、距离度量和数据预处理方法非常重要,以确保KNN算法的性能最优化。
2、原理分析
数学原理
K-近邻(K-Nearest Neighbors,KNN)算法背后的数学原理涉及距离度量、邻居选择和预测的计算。以下是KNN算法的数学原理的详细解释:
- 距离度量: KNN算法中最重要的概念之一是距离度量,它用于衡量样本之间的相似性。常用的距离度量包括欧几里德距离(Euclidean distance)和曼哈顿距离(Manhattan distance)。
- 邻居选择: 对于一个新的数据点,KNN算法计算它与训练数据中所有数据点之间的距离。然后,它选择距离最近的K个数据点作为最近邻居。这些最近邻居可以根据计算的距离值进行排序。
- 预测(分类问题): 对于分类问题,KNN算法会统计这K个最近邻居中每个类别的数量。然后,将新数据点分类为在这些邻居中占多数的类别。
- 预测(回归问题): 对于回归问题,KNN算法会计算这K个最近邻居的目标值的平均值,然后将新数据点的回归预测设置为这个平均值。
在实际应用中,选择适当的K值以及距离度量方法非常重要。K值较小可能会导致模型过拟合,而K值较大可能会导致模型欠拟合。同时,距离度量的选择应根据数据的特点进行调整,以确保能够捕获数据之间的相似性。在高维空间中,可能需要对特征进行标准化以避免某些特征对距离的影响过大。
相关公式及其过程分析
k 近邻法 (k-nearest neighbor, k-NN) 是一种基本分类与回归方法。是数据挖掘技术中原理最简单的算法之一,核心功能是解决有监督的分类问题。KNN能够快速高效地解决建立在特殊数据集上的预测分类问题,但其不产生模型,因此算法准确 性并不具备强可推广性。
k近邻法 的输入为实例的特征向量,对应与特征空间的点;输出为实例的类别,可以取多类。
k近邻法 三个基本要素:k 值的选择、距离度量及分类决策规则。
算法过程:
1, 计算训练样本和测试样本中每个样本点的距离(常见的距离度量有欧式距离,马氏距离等);
2, 对上面所有的距离值进行排序;
3, 选前k个最小距离的样本;
4, 根据这k个样本的标签进行投票,得到最后的分类类别;
输入:训练数据集 :
其中, 为实例的特征向量,
为实例的类别,
输出:实例 x 所属的类 y
(1)根据给定的距离度量,在训练集 T 中找出与x最近邻的个点,涵盖这个 k 点的 x 的邻域记作
(2)在 中根据分类决策规则(如多数决策)决定 x 的类别 y:
其中,为指示函数,即
时
为1,否则
为0
距离度量
特征空间中两个实例点的距离时两个实例点相似程度的反映。
在距离类模型,例如KNN中,有多种常见的距离衡量方法。 如欧几里得距离、曼哈顿距离、闵科夫斯基距离、切比雪夫距离及余弦距离。其中欧几里得距离为最常见。
下面是几种距离的论述:
①欧几里得距离(Euclidean Distance):定义与欧几里得空间中,两点之间或多点之间的距离表示又称欧几里得度量。
二维平面:
三维空间:
推广到在n维空间中,有两个点A和B,两点的坐标分别为:
坐标轴上的值 正是样本数据上的n个特征。
②曼哈顿距离(Manhattan Distance):正式意义为城市区块距离,也被称作街道距离,该距离在欧几里得空间的固定直角坐标所形成的线段产生的投影的距离总和。
其计算方法相当于是欧式距离的1次方表示形式,其基本计算公式如下:
③闵科夫斯基距离(Minkowski Distance):闵氏距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述。
无论是欧式距离还是曼哈顿距离,都可视为闵可夫斯基距离的一种特例。
公式如下:
其中p是一个变参数:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧氏距离;
当p→∞时,就是切比雪夫距离。
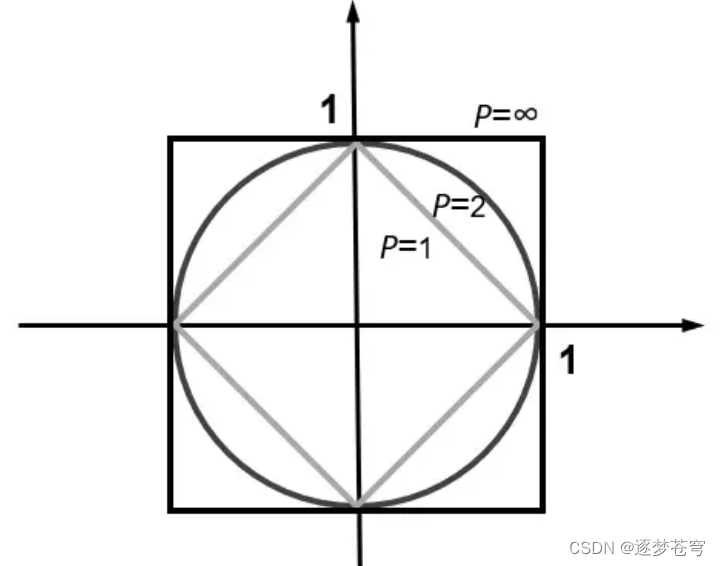
因此,根据变参数的不同,闵氏距离可以表示某一类 / 种的距离。
④切比雪夫距离(Chebyshev Distance):国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
二维平面:
n维空间:
⑤余弦距离:余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个样本差异的大小。
余弦值越接近1,说明两个向量夹角越接近0度,表明两个向量越相似。
几何中,夹角余弦可用来衡量两个向量方向的差异;
机器学习中,借用这一概念来衡量样本向量之间的差异。
公式:
k值选择
k 值的选择会对KNN 算法的结果产生重大影响。
- k 值的减小就意味着整体模型变得复杂,器容易受到由于训练数据中的噪声而产生的过分拟合的影响。
- k 值的的增大就意味着整体的模型变得简单。如果k太大,最近邻分类器可能会将测试样例分类错误,因为k个最近邻中可能包含了距离较远的,并非同类的数据点。
在应用中,k 值一般选取一个较小的数值,通常采用交叉验证来选取最优的k 值。
分类决策规则
根据 "少数服从多数,一 点算一票" 的原则进行判断,数量最多标签类别就是x的标签类别。其中涉及到的原理是"越相近越相似",这也是KNN 的基本假设。
3、API
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
- n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},
- 可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,
- ‘kd_tree’将使用 KDTree。
- ‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。
(不同实现方式影响效率)
4、⭐案例实践
案例:预测签到位置:

数据介绍(train.csv和test.csv ):将根据用户的位置,准确性和时间戳预测用户正在查看的业务。
数据各项介绍:
row_id:登记事件的ID
x / y:坐标
accuracy性:定位准确性
time:时间戳
place_id:业务的ID,这是预测的目标
官网:https://www.kaggle.com/navoshta/grid-knn/data
4.1、分析
- 基本处理
- 缩小数据集范围 DataFrame.query()
- 删除没用的日期数据 DataFrame.drop(可以选择保留)
- 将签到位置少于n个用户的删除place_count = data.groupby('place_id').count()tf = place_count[place_count.row_id > 3].reset_index()data = data[data['place_id'].isin(tf.place_id)]
- 分割数据集
- 标准化处理
- k-近邻预测
4.2、代码
代码如下:
# -*- coding: utf-8 -*-
# @Author:︶ㄣ释然
# @Time: 2023/8/30 23:48
import pandas as pd
from sklearn.model_selection import train_test_split # 将数据集分割为训练集和测试集。
from sklearn.neighbors import KNeighborsClassifier # 实现KNN分类器
from sklearn.preprocessing import StandardScaler # 特征标准化
'''
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数
algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},
可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,
‘kd_tree’将使用 KDTree。
‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。
(不同实现方式影响效率)
'''
def knncls():
"""
K近邻算法预测入住位置类别
:return:
"""
# 一、处理数据以及特征工程
# 1、读取收,缩小数据的范围
data = pd.read_csv("./data/FBlocation/train.csv")
# 数据逻辑筛选操作 df.query()
data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")
# 删除time这一列特征
data = data.drop(['time'], axis=1)
print(data)
# 删除入住次数少于三次位置
place_count = data.groupby('place_id').count()
tf = place_count[place_count.row_id > 3].reset_index()
data = data[data['place_id'].isin(tf.place_id)]
# 3、取出特征值和目标值
y = data['place_id']
# y = data[['place_id']]
x = data.drop(['place_id', 'row_id'], axis=1)
# 4、数据分割与特征工程?
# (1)、数据分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)
# (2)、标准化
std = StandardScaler()
# 队训练集进行标准化操作
x_train = std.fit_transform(x_train)
print(x_train)
# 进行测试集的标准化操作
x_test = std.fit_transform(x_test)
# 二、算法的输入训练预测
# K值:算法传入参数不定的值 理论上:k = 根号(样本数)
# K值:后面会使用参数调优方法,去轮流试出最好的参数[1,3,5,10,20,100,200]
knn = KNeighborsClassifier(n_neighbors=3)
# 调用fit()
knn.fit(x_train, y_train)
# 预测测试数据集,得出准确率
y_predict = knn.predict(x_test)
print("预测测试集类别:", y_predict)
print("准确率为:", knn.score(x_test, y_test))
if __name__ == '__main__':
knncls()执行结果:
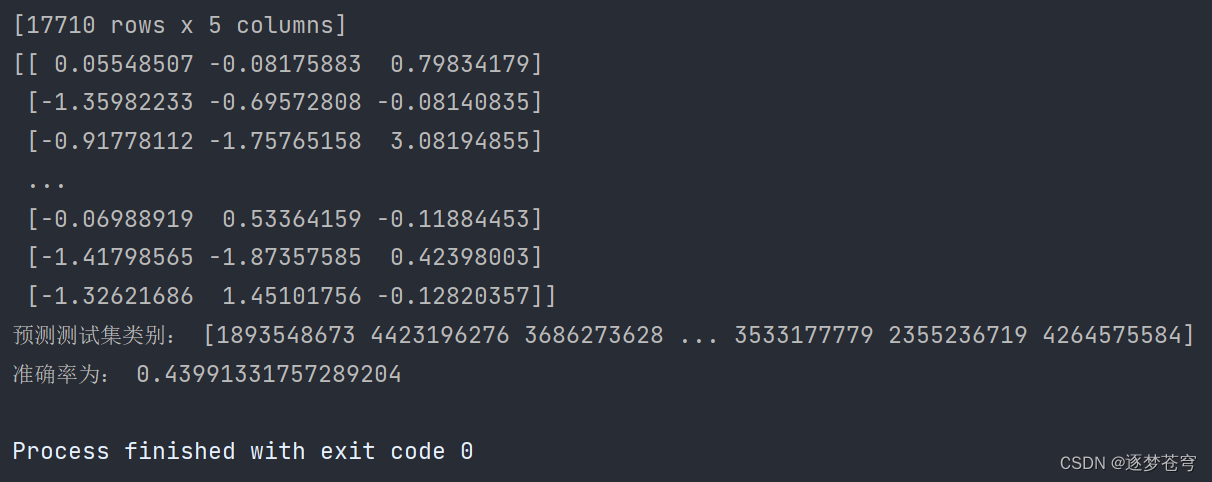
这段代码是一个使用K最近邻(KNN)算法进行分类预测的示例,用于预测移动设备的位置类别。下面逐行解释代码的每个部分:
- 导入必要的包:
- import pandas as pd:导入Pandas库,用于数据处理和分析。
- from sklearn.model_selection import train_test_split:从scikit-learn中导入train_test_split函数,用于将数据集分割为训练集和测试集。
- from sklearn.neighbors import KNeighborsClassifier:从scikit-learn中导入KNeighborsClassifier类,用于实现KNN分类器。
- from sklearn.preprocessing import StandardScaler:从scikit-learn中导入StandardScaler类,用于特征标准化。
- 函数knncls()定义:
- 该函数实现了一个完整的KNN分类流程。
- 数据读取与预处理:
- data = pd.read_csv("./data/FBlocation/train.csv"):从CSV文件读取数据。
- data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75"):对数据进行逻辑筛选,选取特定范围内的数据。
- data = data.drop(['time'], axis=1):删除数据中的时间列。
- place_count = data.groupby('place_id').count():根据位置ID对数据进行分组统计。
- tf = place_count[place_count.row_id > 3].reset_index():选取入住次数超过3次的位置。
- data = data[data['place_id'].isin(tf.place_id)]:筛选出入住次数较多的位置。
- 数据分割与特征工程:
- y = data['place_id']:目标值为位置ID。
- x = data.drop(['place_id', 'row_id'], axis=1):特征值为除位置ID和行ID外的其他特征。
- x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3):将数据集分割为训练集和测试集。
- std = StandardScaler():实例化一个标准化器。
- x_train = std.fit_transform(x_train):对训练集进行标准化操作。
- x_test = std.fit_transform(x_test):对测试集进行标准化操作。
- KNN模型训练与预测:
- knn = KNeighborsClassifier(n_neighbors=1):实例化一个KNN分类器,其中n_neighbors参数设置为1。
- knn.fit(x_train, y_train):训练KNN模型。
- y_predict = knn.predict(x_test):使用训练好的模型进行预测。
- print("准确率为:", knn.score(x_test, y_test)):输出模型在测试集上的准确率。
总体而言,这段代码演示了如何使用KNN算法进行分类预测。它包括数据读取、预处理、特征工程、模型训练和预测等步骤。同时,还使用了StandardScaler进行特征标准化,以及KNN分类器进行预测并计算准确率。
5、K-近邻算法总结
优点:简单,易于理解,易于实现,无需训练
缺点:
懒惰算法,对测试样本分类时的计算量大,内存开销大
必须指定K值,K值选择不当则分类精度不能保证
使用场景:小数据场景,几千~几万样本,具体场景具体业务去测试