目录

题目：

示例：

分析：

代码：

---

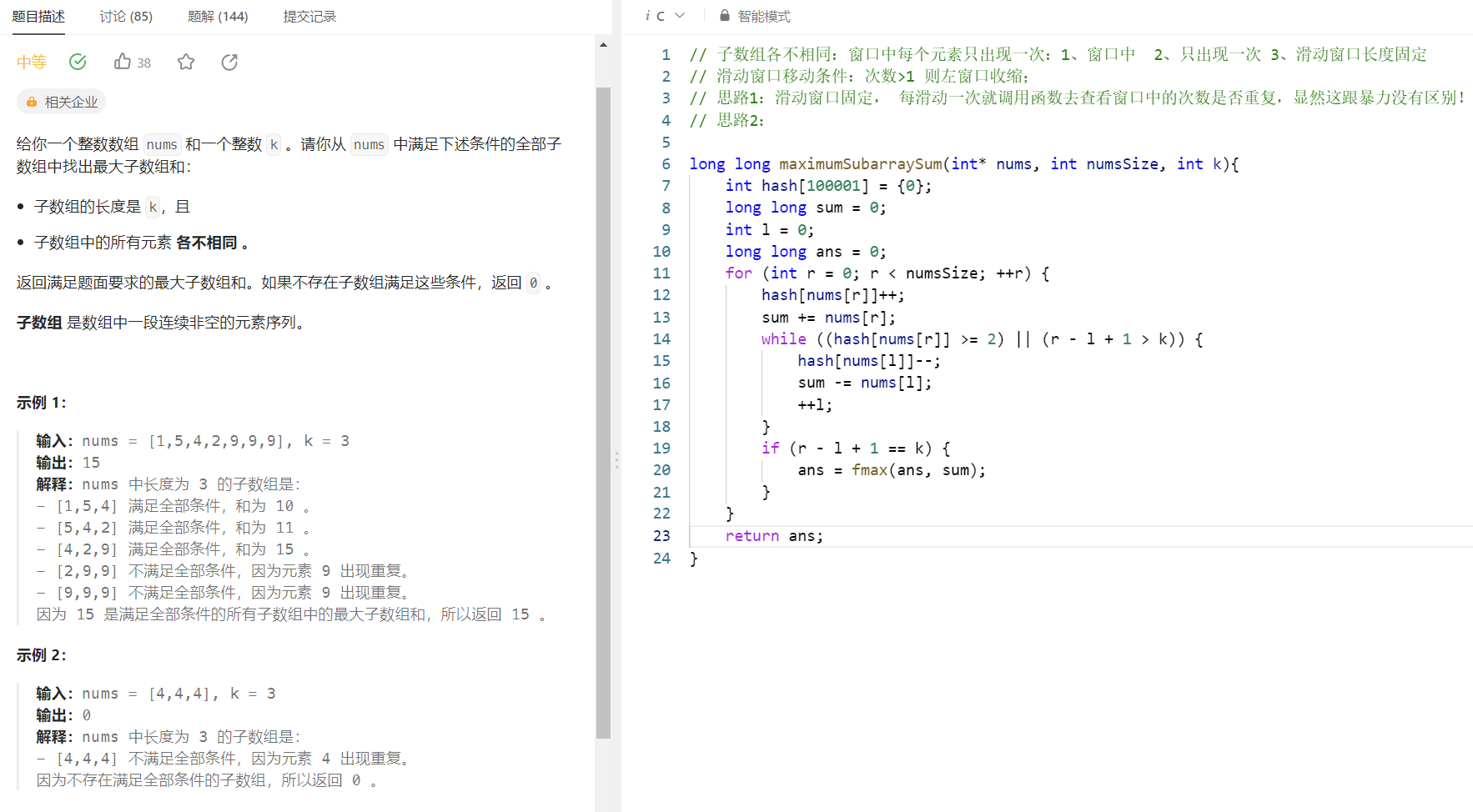
题目：

示例：

分析：

题目给我们一只跳蚤，我们可以操控它前跳 a 格或是后跳 b 格，不能跳到小于0的位置，有一些被禁止的点不能跳到，也不能连续后跳两次，问我们最少跳几次可以让它回家。

一般寻找最短路径我们是用BFS的，不过我更喜欢DFS，所以我这边使用DFS，不过大体的思路是一样的，懂得怎么操作之后，两种方法都是可以自己写出来的。

要写出DFS不难，但是有三个点要注意。

第一点是不能连续后跳两次，所以我们传入递归函数的参数中需要记录上一次是前跳还是后跳。因为不能连续后跳两次，所以如果上一次是后跳，那么我们本次递归就只能前跳。如果上一次是前跳，那我们本次递归就可以后跳以及前跳。

第二点是边界范围，题目要求不能跳到小于0的位置，所以左边界是0。而右边界，由于我们可以跳到目标点的后面再后跳回来，所以我们右边界不能定为目标点。我原本以为一次最多就后跳b格，所以我把右边界设为了目标值+b，但是是行不通的。最终右边界设置为6000就可以了，因为题目有给出限制，目标点、a、b最大都是2000，那么把他们加起来就是6000，稍微思考一下就可以知道在最极端的情况下我们也不需要跳到6000往后的点，所以右边界设为6000即可。

不过还是有大佬把右边界的具体范围推导出来了，比较复杂，感兴趣的小伙伴可以自行去本题的题解里查看。

最后一点就是剪枝，因为我们可能会跳到重复的一个点，进而陷入死循环，所以我们需要在递归的时候将往前跳的落脚点设为被禁止的点，这样就不会重复跳到同一个点了。

不过往后跳的点不需要，因为如果是后跳跳到了一个点，那么接下来就只能是往前跳了。如果设置为了禁止点，那么如果后续递归中是往前跳跳到了这个点，那么本来是可以在这个点上往后跳的，但是由于设置为了禁止点，所以就会退出循环，这样就少了一种可能性，也就有可能会错失答案。

 

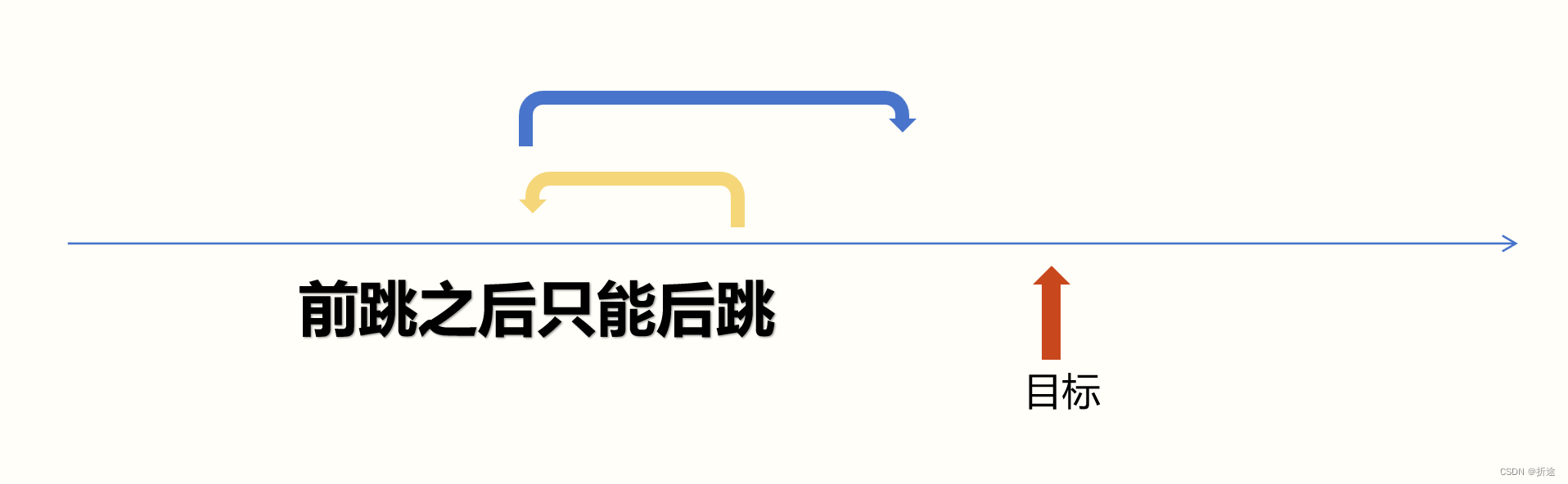
可能会有小伙伴会有疑问，后跳的点不设为禁止点不会进入死循环吗？

答案是不会的，因为如果下次是前跳到这个点了，那么还是会被设为禁止点。然而是不可能是后跳到重复的点，因为不能重复后跳两次，能够后跳到这个点的地方，一定是前跳到那个地方的，也就是会被设为禁止点，那么也就不可能再重复后跳到同一个点了。

所以本质上是让一个点最多能重复跳到两次，第一次是后跳到达，最后一次是前跳到达。

代码：

class Solution {
public:
    int res=INT_MAX;
    void find(unordered_set<int>&forbidden,int a,int b,int cur,int x,int temp,bool flag){
        if(cur<0||cur>6000||temp>=res) return;  //设置边界
        if(cur==x){
            res=min(res,temp);
            return;
        }
        //前跳
        if(!forbidden.count(cur+a)){    //如果下一个跳跃点不被禁止,那么跳跃
            forbidden.insert(cur+a);    //避免进入死循环,将跳跃点设为禁止点
            find(forbidden,a,b,cur+a,x,temp+1,true);
        }
        //后跳
        if(!forbidden.count(cur-b)&&flag){  //如果后跳的点不被禁止,并且上一次不是后跳,那么跳跃
            find(forbidden,a,b,cur-b,x,temp+1,false);
            //不将后跳的点设为禁止点,可能会错过答案.因为
        }
    }
    int minimumJumps(vector<int>& forbidden, int a, int b, int x) {
        unordered_set<int>s(forbidden.begin(),forbidden.end()); //将禁止点集合转为set方便查询
        find(s,a,b,0,x,0,true);
        return res==INT_MAX?-1:res;
    }
};