题目

https://www.matiji.net/exam/brushquestion/1/4347/179CE77A7B772D15A8C00DD8198AAC74?from=1

题目大意：

给定一个无向图，有两个人往同一个目的地走，分别消耗体力TE、FE。如果他们到某个点汇合了，然后一起走向目的地，那么消耗的体力就会减少S。求他俩到景点 N 时，所需要的总消耗最少是多少？

思路

如下图所示，两个人F和T要先走到同一个汇合点x，然后在一起往目的地N点走。（图片来自【2023百度之星第一场题解】嘉宾：NOI、IOI金牌周航锐）

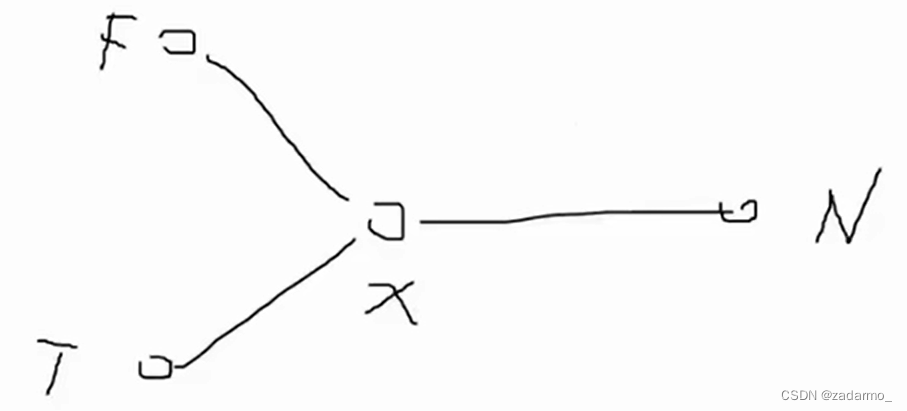
当汇合点x确定的时候，总体力 = F走到x的最短路径 * FE + T走到x的最短路径 * TE + x到N的最短路径 * （FE+TE-S）。由于无法确定哪个x是最优的汇合点，所以需要遍历所有的点，分别求出总体力，最后取一个最小值。

所以思路如下：

1. 分别求F、T、N到所有点的最短距离
2. 遍历所有点（汇合点），对于每个点，计算需要的总体力
3. 取所有总体力的最小值

代码

#include<bits/stdc++.h> 

using namespace std;

const int n = 40010;

int TE, FE, S;
int T, F, N, M;

vector<int> v[n];  // 邻接表 
int d[3][n]; // 小度、度度熊、终点到每个点的最短距离

void bfs(int dist[], int src)  // 求src点到每个点的最短距离
{
	/* bfs求最短路的模板 */
    int q[n];

    for(int i = 1; i <= N; i ++ ) dist[i] = -1;  // 初始化为-1，表示src不能到达i

    int hh = -1;
    int tt = 0;
    dist[src] = 0; 
    q[++hh] = src;

    while (hh <= tt)
    {
        int head = q[hh++];
        for (auto x : v[head])
        {
            if (dist[x] == -1)
            {
                dist[x] = dist[head] + 1;
                q[++tt] = x;
            }
        }
    }
}

int main( )
{
    cin >> TE >> FE >> S;
    cin >> T >> F >> N >> M;

    for(int i = 0; i < M; i ++ ) 
    {
        int a, b;
        cin >> a >> b;
        v[a].push_back(b);
        v[b].push_back(a);
    }

	// 分别计算T、F、N到所有点的最短路径
    bfs(d[0], T);
    bfs(d[1], F);
    bfs(d[2], N);

    long long ans = 1e18;
    for (int i = 1; i <= N; i ++ ) 
    {
    	// 这里要判断是否等于-1。如果等于-1，说明当前汇合点i不能到达T、F、N中的某个点
        if (d[0][i] != -1 && d[1][i] != -1 && d[2][i] != -1)
        {
            long long distance = 1ll * d[0][i] * TE + 1ll * d[1][i] * FE + 1ll * d[2][i] * (TE + FE - S);
            ans = min(ans, distance);
        }
    }

    if (ans == 1e18) cout << -1 << endl;
    else cout << ans << endl;

    return 0;
}

总结

BFS求解最短路径的代码：

const int N = 100010; // 题目所给的最大的点的个数
vector<int> v[N]; // 邻接表，用来存图

void bfs(int dist[], int src) 
{
	/* bfs求最短路的模板 */
    int q[N];

    // 初始化距离为-1，表示最开始src不能到达所有点
    for(int i = 1; i <= N; i ++ ) dist[i] = -1; 
	
	// 将src入队，并将最短距离赋值为0
    int hh = -1;
    int tt = 0;
    dist[src] = 0; 
    q[++hh] = src;

	// bfs
    while (hh <= tt)
    {
    	// 取队首
        int head = q[hh++];

		// 遍历队首的邻接点
        for (auto x : v[head])
        {
            if (dist[x] == -1)
            {
                dist[x] = dist[head] + 1;
                q[++tt] = x;
            }
        }
    }
}