1、lorentz峰值拟合

发光光谱是一种用于表征二维半导体材料光学性质的重要技术，它可以反映出材料中的载流子密度、缺陷态、激子束缚能等信息。

由于二维半导体材料的厚度极其薄，其发光信号往往很弱，且受到基底、环境和测量设备等因素的干扰，因此需要对发光光谱进行合理的数据处理和分析，以提取出准确和可靠的物理参数。

Lorentz峰值拟合是一种常用的数据处理方法，原理是假设每个峰值都是由一个或多个激子态产生的，每个激子态都可以用一个复数表示其能量和寿命，然后利用最小二乘法求解出最佳拟合参数，可以用来描述二维半导体材料发光谱的单个或者多个峰值，从而得到峰值位置、强度、宽度等参数。

对光谱进行Lorentz峰值拟合可以有效地提高数据质量和分析精度，能够更精确地确定激子峰的位置和强度，从而研究材料的特征。

函数形式如下：

$$L(x)=\frac{A}{\pi }\frac{\frac{1}{2}\Gamma }{(x-x_0{)}^2+(\frac{1}{2}\Gamma {)}^2}$$

其中，x是光谱的横坐标（波长或波数），$x_0$是峰值的位置，A是峰值的幅度，$\Gamma$是峰值的半宽度（与峰值的展宽程度有关）。

拟合过程通过调节参数$x_0$、A和$\Gamma$来使得lorentzian函数尽可能拟合实际的光谱峰值。

注意：我的csv文件，第一列为波长，第二列为光子数（光强）。

2、单峰拟合

# 在Python中，可以使用科学计算库SciPy来实现对光谱数据的Lorentz峰值拟合。
# 我们首先定义了一个Lorentzian函数，并生成了一个模拟的光谱数据，其中加入了一些随机噪声。
# 然后，我们使用curve_fit函数进行拟合，其中p0参数是初始猜测的参数。
# 最后，我们绘制了原始数据和拟合结果的图像，并打印出拟合得到的参数。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import pandas as pd

# 定义Lorentzian函数
def lorentzian(x, x0, A, gamma):
    return A * gamma**2 / ((x - x0)**2 + gamma**2)

# # 生成模拟的光谱数据
# x_data = np.linspace(500, 700, 200)
# true_params = [600, 1000, 20]  # 真实的参数：x0：峰值位置； A：峰值幅度； gamma：峰值的半宽度
# y_data = lorentzian(x_data, *true_params) + np.random.normal(0, 50, len(x_data))  # 加入噪声
# wavelength = x_data
# intensity = y_data


# 读取光谱数据
file_path = r'your-path-of-csv'
data = pd.read_csv(file_path, header=None)

wavelength = data.iloc[:, 0]
intensity = data.iloc[:, 1]


# 进行拟合
# 初始猜测的参数，根据实际数据和仿真结果对initial_guess进行调整
# 注意：如果遇到下面的错误：
# RuntimeError: Optimal parameters not found: Number of calls to function has reached maxfev = 1400.
# 默认情况下curve_fit函数的最大迭代次数是1400次，如果出现这样的报错，
# 可以尝试提供更合理的初始猜测值，有时候初始猜测值不合适可能会导致拟合无法收敛。
initial_guess = [1170, 100, 20]  # 初始猜测的参数：x0, A, gamma
fit_params, _ = curve_fit(lorentzian, wavelength, intensity, p0=initial_guess)

# 绘制拟合结果
plt.plot(wavelength, intensity, label='Original Spectrum')
plt.plot(wavelength, lorentzian(wavelength, *fit_params), color='red', label='Fit peak: ' + "{:.1f}".format(fit_params[0]))
plt.legend()
plt.xlabel('Wavelength')
plt.ylabel('Intensity')
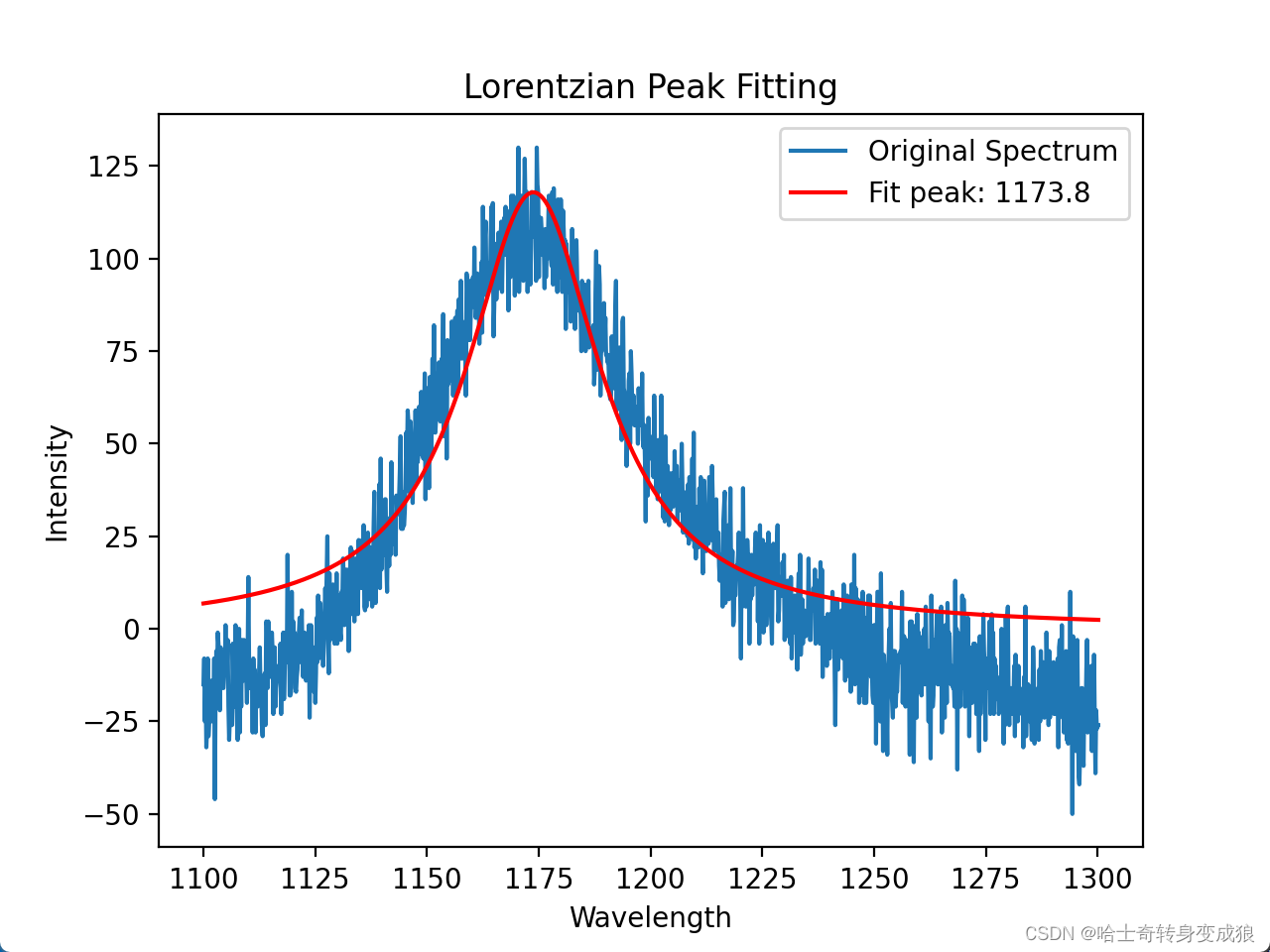
plt.title('Lorentzian Peak Fitting')
plt.show()

print('Fit parameters:', fit_params)

输出:

Fit parameters: [1173.7909121   117.90768115   18.34664239]

2、双峰拟合

在单峰的基础上增加一个双洛伦兹函数：

# 定义双Lorentzian函数作为拟合模型
def double_lorentzian(x, x1, A1, gamma1, x2, A2, gamma2):
    return lorentzian(x, x1, A1, gamma1) + lorentzian(x, x2, A2, gamma2)

然后再进行拟合：

fit_params, _ = curve_fit(double_lorentzian, wavelength, intensity, p0=initial_guess)

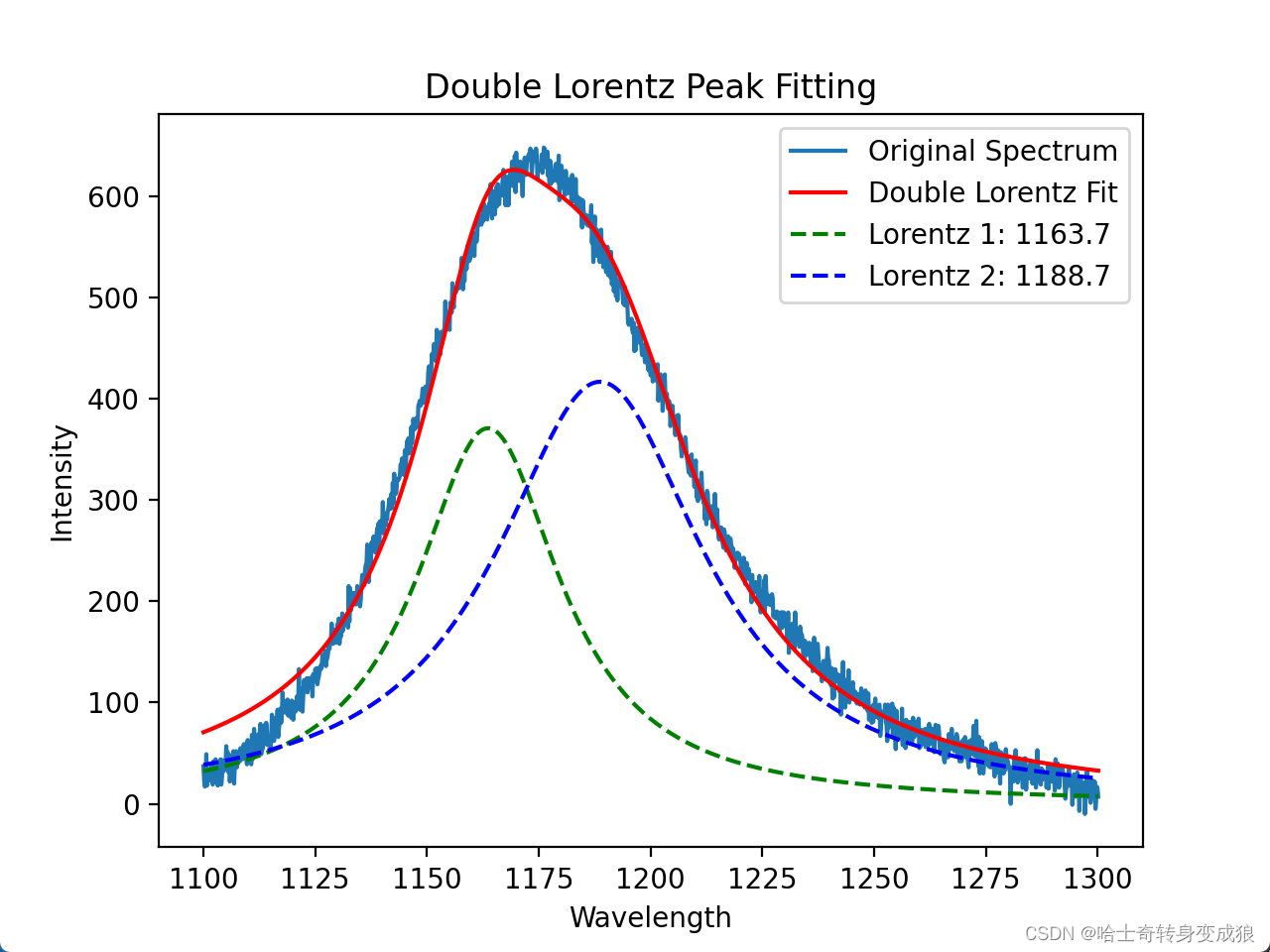
最后打印出结果：

Fit parameters: [1163.66742694  370.85710156   19.65005682 1188.70437071  416.71761075
   28.27593917]